相干OFDM系统中的频率偏移补偿算法的研究毕业论文
2020-02-19 20:37:57
摘 要
本文借助软件MATLAB对于正交频分复用系统中频率偏移补偿算法进行了模拟仿真,对于正交频分复用的几种常见的频率偏移补偿算法的仿真结果进行了分析和比较,所得到的结果对于正交频分复用系统中频率偏移的补偿具有重要的指导意义。
论文主要研究了正交频分复用的基本原理、几种常见的频率偏移补偿算法的原理、(具体包括基于导频信号的频率偏移补偿算法、基于循环前缀的最大似然的频率偏移补偿算法、基于训练序列的频率偏移补偿算法)以及其具体的实现步骤和这些算法在MATLAB中的仿真结果、同时论文还对于上述算法的优缺点进行了研究。
研究结果表明:频率偏移对于OFDM系统有破坏性非常大,采用频率偏移补偿算法可以有效的解决频率偏移对于OFDM系统的影响。
本文的特色:本文从理论推导出发,通过严密的数学公式推导阐述了几种频率偏移补偿算法的原理,同时本文联系实际对算法进行了仿真,所以本文有一定的实用性。
关键词:正交频分复用;频率偏移;循环前缀;训练序列
Abstract
In this paper, the frequency offset compensation algorithm in orthogonal frequency division multiplexing system is simulated by software MATLAB. The simulation results of several common frequency offset compensation algorithms in orthogonal frequency division multiplexing system are analyzed and compared. The results obtained have important guiding significance for frequency offset compensation in orthogonal frequency division multiplexing system.
This paper mainly studies the basic principle of orthogonal frequency division multiplexing, the principle of several common frequency offset compensation algorithms, including frequency offset compensation algorithm based on pilot signal, maximum likelihood frequency offset compensation algorithm based on cyclic prefix, frequency offset compensation algorithm based on training sequence, and its specific implementation steps, as well as the imitation of these algorithms in MATLAB. The real results and the advantages and disadvantages of the above algorithms are also studied in this paper.
The results show that frequency offset is very destructive to OFDM system, and frequency offset compensation algorithm can effectively solve the impact of frequency offset on OFDM system.
The characteristics of this paper: Starting from theoretical deduction, this paper expounds the principles of several frequency offset compensation algorithms through rigorous mathematical formula deduction. At the same time, this paper simulates the algorithm with practice, so this paper has a certain practicability.
Key words: OFDM;Frequency deviation;Cyclic prefix;training sequent
目 录
1 绪论 1
1.1 课题研究的背景与意义 1
1.2 国内外研究现状 1
1.3 本论文研究的主要内容 3
2 OFDM技术简介 4
2.1 OFDM的基本原理 4
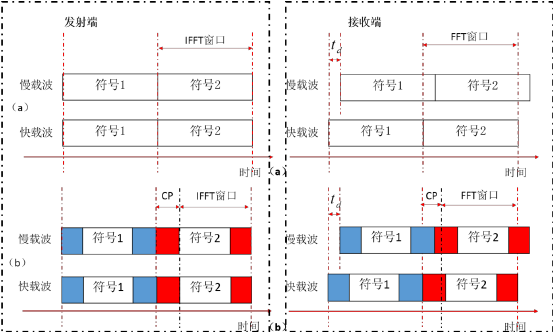
2.2 OFDM的循环前缀 7
2.3 OFDM系统模型 9
3 OFDM系统频率偏移补偿算法 10
3.1 基于导频信号的频率偏移补偿算法 10
3.2 基于训练序列的频率偏移补偿算法 11
3.3 基于循环前缀的频率偏移补偿算法 14
4 频率偏移补偿算法的仿真 17
4.1 仿真平台简介 17
4.2 频率偏移补偿算法的仿真 18
5 总结与展望 30
参考文献 31
致 谢 32
1 绪论
1.1 课题研究的背景与意义
随着世界进入信息化时代,我国的经济和社会在高速的发展,在当今社会,人们每天进行着大量的信息交换,信息交换的用户越来越多,据调查我国有接近7亿数量的网民[1],与此同时用户对信息传递的质量要求越来越来高,例如高速下载,视频会议,大型游戏等,所以在当今社会,频率资源、通信容量这些通信系统中的重要指标遭受着更大的挑战,在这种情况下,在通信系统的各个领域,通信工作者都在尝试使通信容量变得更大以及使响应时间变得更快的方向发展。
最初的调制方式是模拟调制方式,这主要是因为模拟调制简单,后来因为数字技术的兴起,数字技术展现了它独特的优势,所以后来数字调制技术占据了主导的地位,在当今社会,通信系统的调制技术可以由单载波调制技术和多载波调制技术两种技术组成[2],单载波调制技术就是把我们想要传输的信号调制到一个载波上传输出去,之所以要进行调制是因为原始的基带信号无法在无线信道中传输,根据天线理论,只有当发射信号的波长与天线的尺寸相比拟时,才有足够的能量辐射出去,原始信号的频率太低,波长太长,另外也只有在高频频段才有足够的频率资源进行传输,多载波调制技术就是利用多个子载波来传输我们想要传输的信号,其要求每个子载波之间要有一定的频率间隔,这主要是为了防止不同载波之间的相互干扰,传统的多载波调制技术要求子载波频率间隔非常大,这样一来非常浪费珍贵的频率资源,没有做到对频率资源的充分利用,而正交频分复用技术(OFDM)也是一种多载波调制技术,它与传统的多载波调制技术不同的是它的子载波频谱中间相互重叠,OFDM技术在通信系统中的应用非常广泛,与此同时OFDM技术同样也是现在通用的4G通信系统中的关键技术,OFDM技术凭借其频谱利用率高、抗色散能力强、以及其非常好的灵活性等优点成为现在最为广泛利用调制技术,虽然OFDM技术拥有上述很多优点,但是其却具有一个致命的缺点,OFDM技术对于子载波的频率的偏差非常敏感,一点偏差可能引起解调的失败,所以我们必须对OFDM技术的频率偏移的补偿算法进行研究,这样我们才能很好的使用OFDM技术。
1.2 国内外研究现状
OFDM技术作为现在通信系统中的关键技术,其对于子载波的频率偏移非常敏感,所以对于其频率偏移补偿算法(FOC)的研究很早就开始了,前面说过OFDM技术中的子载波频谱之间相互重叠,为了保证其不会产生子载波之间相互干扰,要求子载波频率之间相互正交,但是由于信道传输以及其他方面的影响会导致子载波频率发生偏移,从而不能满足子载波之间的相互正交,这样在接收端解调信号时会发生混乱乃至完全无法正常解调出来,所以我们必须对OFDM系统的频率偏移进行估计和补偿。
首先我们介绍的是数据辅助型的频率偏移补偿算法,其中最为经典的算法就是Schmidlamp;Cox算法[3],通过查阅资料我们发现目前频率偏移补偿算法多是将系统的频率偏移量分成两个部分进行研究,一个为整数部分的频偏,另一个为小数部分的频偏。Schmidlamp;Cox算法主要是利用了训练序列来进行频率偏移的估计,这个算法包括两个训练序列,其第一个序列用于小数部分的频偏估计,其基本原理就是在一个时间窗口内利用第一个训练序列前后部分相同,使这两个相同的部分共轭相乘求和然后找出最大值,我们可以利用这个最大值的位置进行小数部分频偏的估计。而对于整数部分的估计,该算法采用快速傅里叶变换(FFT)将信号由时域转到频域,利用前后两个训练序列所对应的偶数子载波之间会因为整数部分频偏而存在一个确定相位变化的原理,我们可以采用移位运算得到相位变化的值,由这个值我们可以得到整数部分频率偏移。由上面的介绍,我们可知Schmidlamp;Cox算法可以完成OFDM系统的频率偏移的估计,但是研究却发现其对于小数部分频偏的估计效果比整数部分频偏的估计效果要好,这依赖于不同的训练序列,所以正是基于这一点后来产生了很多其他的算法。在2011年,美国NEC实验室提出利用两组不一样的训练序列组合起来估计频偏,与此同时采用导频信号来反映频率偏移值。2012年,Xian Zhou等人采用了一种新型的训练序列,这种新型的训练序列是由大量的重复单元形成的,这种算法的优点在于可以通过减小重复单元的大小使其估计的频率偏移范围越来越大,但是重复单元不可能无休止的减小,所以这种估计是有缺陷的,因为重复单元的长度有最小值。2015年,纽芬兰纪念大学的工作人员提出CAZAC算法,这种算法的频率偏移的估计范围比较大,同时其准确性与前面的算法相比也有所提高,而且其利用率高。
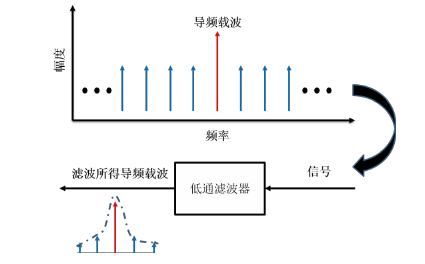
上面讲的是数据辅助性的FOC算法,在多年的研究中,还有采用导频信号进行频率偏移的估计,所谓导频信号就是基站连续发射未经调制的直接序列扩频信号[4],而基于导频的FOC算法就是在载波中插入以子知频率并且功率较大的信号,然后在接收端滤出已知的导频信号,通过比较在发射端的导频信号和在接收端的导频信号就可以得到频率偏移值,其中最简单的算法就是在接收端滤出已知子载波,2008年,Fred Buchali在OFDM信号的频谱中心放置导频信号,此后德国人采用RF-Pilot提高了系统的信噪比。
在OFDM信号中会插入循环前缀(CP),基于CP的FOC算法是利用CP与有效信号之间的相关性,通过概率论上的最大似然(ML)的方法对于频率偏移进行估计,近年来,研究人员正尝试着把不同的算法组合起来形成一种新型的FOC算法,2010年,Z.Wang等人把CP与训练序列这两种频率偏移估计的方法结合起来进行频偏估计,上面我谈论到很多FOC算法,这些算法在后文中还会进行详细的阐述。
1.3 本论文研究的主要内容
本论文主要研究相干OFDM系统中频率补偿算法的问题,在这个论文中,我着重研究了几种不同的频率偏移补偿算法的原理以及如何实现这些算法具体步骤,并且采用MATLAB仿真平台对经典的频率偏移补偿算法进行仿真,本论文的主要内容如下:
第一章是绪论,我主要从实际出发,讲解了本次论文课题的研究背景也就是我们为什么要研究这个课题,在第一章我还介绍了这个课题现在国内外的研究情况。
第二章是OFDM技术简介,详细的介绍了OFDM技术的基本原理,从理论上论证了OFDM信号如何保持信号在时域的正交以及在频域的子载波的最小间隔,同时我介绍了循环前缀(CP)的作用,在最后给出OFDM系统的模型。
第三章是OFDM系统的频率偏移补偿算法,论文首先讲述了频率偏移对于相干OFDM系统的严重危害,然后主要介绍了几种频率偏移补偿算法的原理和实现的具体过程,这几种算法包括基于导频信号的频率偏移补偿算法、基于训练序列的频率偏移补偿算法、基于循环前缀的频率偏移补偿算法。并对这几种算法的优缺点和应用的范围进行简单的叙述。
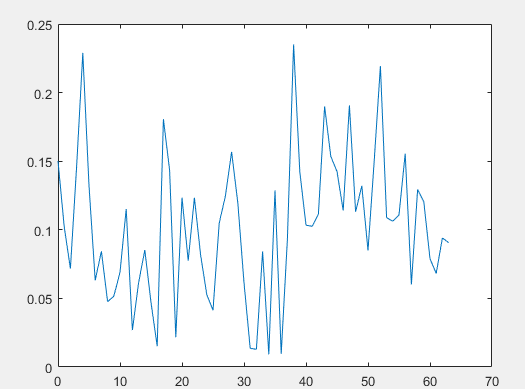
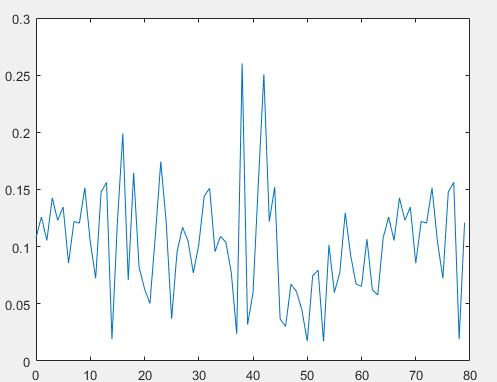
第四章是频率偏移补偿算法仿真,在这一章中,论文首先介绍了本次的仿真平台MATLAB,介绍了MATALB在通信领域的强大作用,然后对基于循环前缀的最大似然估计的频率偏移补偿算法以及基于训练序列的频率偏移补偿算法进行了仿真,给出了仿真的具体过程以及详细的操作步骤,并且给出了仿真的结果,论证了算法的有效性和可行性。
第五章是总结与展望,在这一章中,我对论文进行了的详细的总结,并且对于频率偏移补偿算法的未来研究方向做出了展望。
2 OFDM技术简介
2.1 OFDM的基本原理
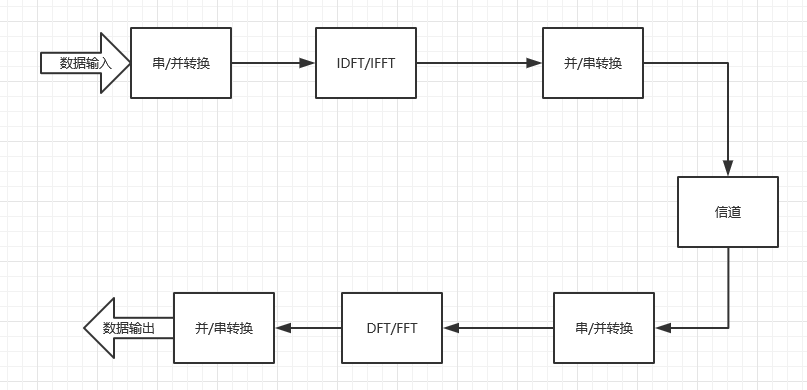
OFDM技术是一种多载波调制技术,其调制框图如下图所示,其中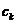 为经过串并转换之后的并行传输信号,
为经过串并转换之后的并行传输信号,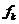 为不同子载波的频率,从图中可以看出原始信号经串并转换后的并行信号个数应该与子载波个数相等[5],每一个并行信号与其相应的子载波相乘后,最后相加在信道中传输,在接收端解调出来,OFDM技术可以将高速传输的数据信号通过串并转换变为大量并行的低速子数据流,然后将这些低速的子数据流分别调制到各自对应的子信道上进行传输,这样一来会使得每个子信道上的信号带宽减小,从而可以实现其小于信道的相关带宽,所以我们可以把信道认为理想信道,从而可以消除码间干扰,并且由于每个子信道的带宽的减小,信道均衡变得容易。
为不同子载波的频率,从图中可以看出原始信号经串并转换后的并行信号个数应该与子载波个数相等[5],每一个并行信号与其相应的子载波相乘后,最后相加在信道中传输,在接收端解调出来,OFDM技术可以将高速传输的数据信号通过串并转换变为大量并行的低速子数据流,然后将这些低速的子数据流分别调制到各自对应的子信道上进行传输,这样一来会使得每个子信道上的信号带宽减小,从而可以实现其小于信道的相关带宽,所以我们可以把信道认为理想信道,从而可以消除码间干扰,并且由于每个子信道的带宽的减小,信道均衡变得容易。
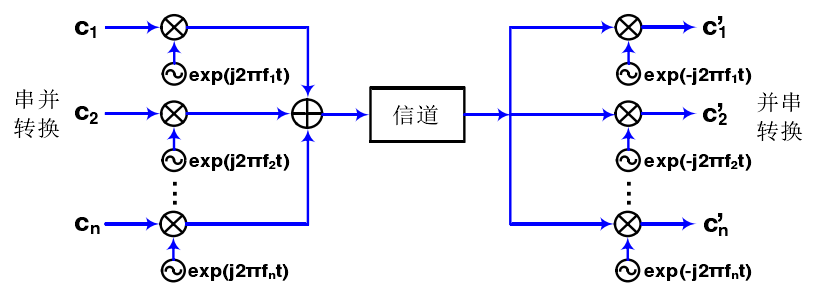
图2.1 OFDM系统调制解调图
与传统的多载波调制技术相比,OFDM系统中子载波频谱之间相互重叠,这极大的提高了频谱效率[6],在传统的多载波调制技术中,信道之间的频率间隔通常是信道传输速率的几倍以上,下面我将给出OFDM子载波的频谱图。
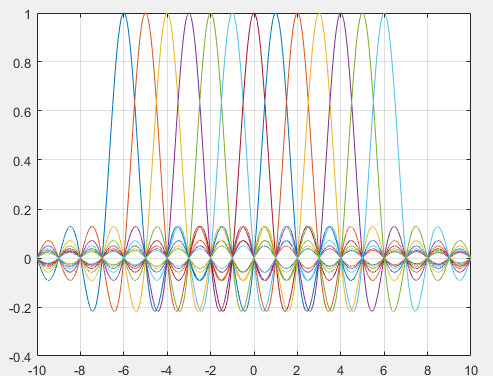
图2.2 子载波的频谱图
我们可以从上图可以清楚的看出,子载波的频谱之间有明显的重叠部分,那么怎样保证不会发生干扰,原因在于这些子载波在时域上是正交的,下面我将采用数学的方式来推到载波频率所满足的条件。设在一个OFDM系统中有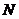 个子载波,每个子载波可以设为
个子载波,每个子载波可以设为



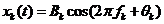
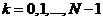 (2.1)
(2.1)
在上式中: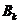 为第
为第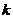 路子载波的振幅,
路子载波的振幅,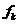 为第
为第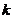 路子载波的频率,
路子载波的频率,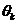 为第
为第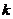 路子载波的初相位,因此整个传输信号可以表示为
路子载波的初相位,因此整个传输信号可以表示为
 (2.2)
(2.2)
为了使上述的信号相互之间不影响,从而使其在接收端可以正确的分离出来,要求它们在时域正交[7],在码元持续时间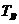 内任意两个子载波正交的条件为
内任意两个子载波正交的条件为
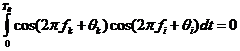 (2.3)
(2.3)
式(2.3)可以改写成
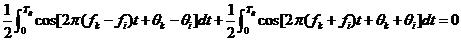 (2.4)
(2.4)
上式等于0的条件为
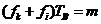 ,
,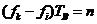 (2.5)
(2.5)
其中,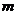 和
和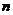 要求为整数,并且
要求为整数,并且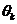 和
和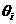 可以任意取值。由式(2.5)可得
可以任意取值。由式(2.5)可得
 ,
,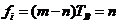 (2.6)
(2.6)
这样子载波的频率就必须服从
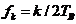 (2.7)
(2.7)
式中: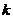 为整数,所以我们可以得到子载波间隔为
为整数,所以我们可以得到子载波间隔为
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: