英语原文共 5 页，剩余内容已隐藏，支付完成后下载完整资料

---

在噪声环境下遥感勘测系统中

BPSK调制解调器的FPGA实现

作者：Pero Krivic,Goran Stimac

翻译人：徐婷婷

摘要:由于固有的高噪声免疫力和低误码率，BPSK调制解调技术被广泛应用在工业遥感勘测系统的数字通信噪声信道中。可编程逻辑器件实现BPSK调制解调器的最关键部分，是解调器的设计。我们研究了在BPSK解调过程中两种常用解调方法的特征，这两种方法分别是基于复解调原理的BPSK非相干解调、基于利用内部锁相环（PLL）和数字控制振荡器（NCO）实现同步载波的BPSK相干解调，并且这两种方法都可以在高效FPGA上实现。在本次研究中，我们利用相关的滤波器和积分器实现码元同步。对于噪声环境下的健壮性和FPGA实现的复杂性这两方面，我们比较了上述两种方法的所有相关特性。

关键字：遥感勘测系统，BPSK调制技术，相干/非相干解调，码元同步

1 简介

本文中我们的研究目的是，开发一种特定数字通信系统，该通信系统主要为在直流电源线上进行电力线通信（PLC）提供方法。这个问题的解决方法应用在其他相似问题中也可以较容易实现，比如无论何时遥感勘测系统需要在噪声信道进行交流耦合时均可采用这一方法。一种有着和本文研究相同目标的直流电力线通信系统已经在麻省理工学院实现^[1]。

通信系统的物理层是基于BPSK调制解调原理的，该部分在低信噪比时呈现出低误码率的特征^[2]。在本文中，我们研究两种广为人知的解调方法，也即BPSK的相关解调和非相干解调。对于上述每种解调方法，与之适配的FPGA实现算法已经被开发出来。非相干解调算法提供了一种非常简单的FPGA实现方法，而与之相比较，相干解调算法的结果则在各个性能指标上都较好，但是其代价为较复杂的实现方法。本文中所采用的非相关解调方法解决了由于使用简单复解调过程中产生的问题。同时，相比于更加复杂的相干解调方法，这种非相干解调具有很明显的FPGA低使用率，这是因为相干解调需要用到一种拥有内部锁相环（PLL）和数控振荡器（NCO）的同步载波。

尽管这两种解调方法的原理众所周知，但是在实际操作时，在FPGA硬件平台上实现相关数学公式时还有许多困难。针对此问题，我们参考了大量的文献：一种关于FPGA技术的Costas环可能实现方案在文献[3]中提出；另一种采用CIC抽取的方法在文献[4]中提出；一些解决方案使用DSP控制器，比如文献[5]；也有一些使用SoC实现Costas环，比如文献[6]。

我们的研究目标是开发一种在直流电源线路上进行电力线通信（PLC）的方案，并且可以在FPGA上直接实现。我们遇到的主要问题是，缺少介绍在FPGA上实现有效BPSK调制解调过程中所有重要步骤的文献。我们也开发了在前文中介绍的相关检测方法。本文中，我们首先介绍了这两种解调方法的数学背景，然后阐述了我们的FPGA实现方案以及仿真结果。并且最后在仿真结果中，就噪声环境下的健壮性和FPGA实现的复杂性而言，我们比较了上述两种方法的所有相关特性。

2 BPSK 调制解调模型

在本章中，我们介绍了BPSK调制解调的理论背景和数学模型，这些对于理解我们所提出方案的实现原理十分有必要。本章对两种解调方法进行简单概述，而实现原理中更加深层的数学细节可以在相关参考文献中找到。

2.1 相关解调

2.1.1 同步载波

BPSK相干解调实现的第一步是创建同步载波。而为了实现同步载波，需要产生一个和载波同相位的辅助信号。同步载波的过程基于Costas环^[2]。Costas环是一种能在调制信号改变极性时使用一个合适相位锁定的特殊锁相环(PLL)。Costas环的框图如图1所示，更加详细的说明可参考文献[2]和[8]。

低通滤波器

数控振荡器

环路滤波

90度

低通滤波器

图1 Costas环原理框架图

Costas环的目的是提取解调信号在循环中的“同相”分支。为了实现这一目标，数字控制振荡器必须产生一个相位与输入信号相同的正弦信号。数字控制振荡器可以采用直接数字合成法（DDS）在FPGA上实现。数字控制振荡器由环路滤波器的反馈控制。再将输入信号和I、Q支路的数字控制振荡器支路信号相乘，并将两个支路的结果信号进行低通滤波之后，在输入信号和数字控制振荡器信号之间会产生相位差。在I、Q支路上乘以滤波信号后，相位差增加一倍（这就是为什么把右边的乘数成为相位倍增值），并且得到的误差信号被用来控制振荡器。Costas环反馈环路中的滤波器设计对于解调成功起到至关重要的作用，这一部分在文献[9]中有所描述。在这个设计中，我们开发了环路滤波器作为零级滤波器（也即增益块）。该滤波器的增益值是通过Z域的系统稳定性所决定，这个在文献[9]中也有所描述。

2.1.2 码元同步

锁相环的输出信号其实是一种解调信号，也即噪声的非归零（NRZ）波形。从该信号中划分和提取数据位是十分有必要的，因为这有利于在接收信息中解码出实际数据中的有效载荷。在工业噪声环境中，由于大噪声和脉冲干扰的存在，这可能是一个困难的任务。而确保精确读取信息位的过程就被称作为码元同步。

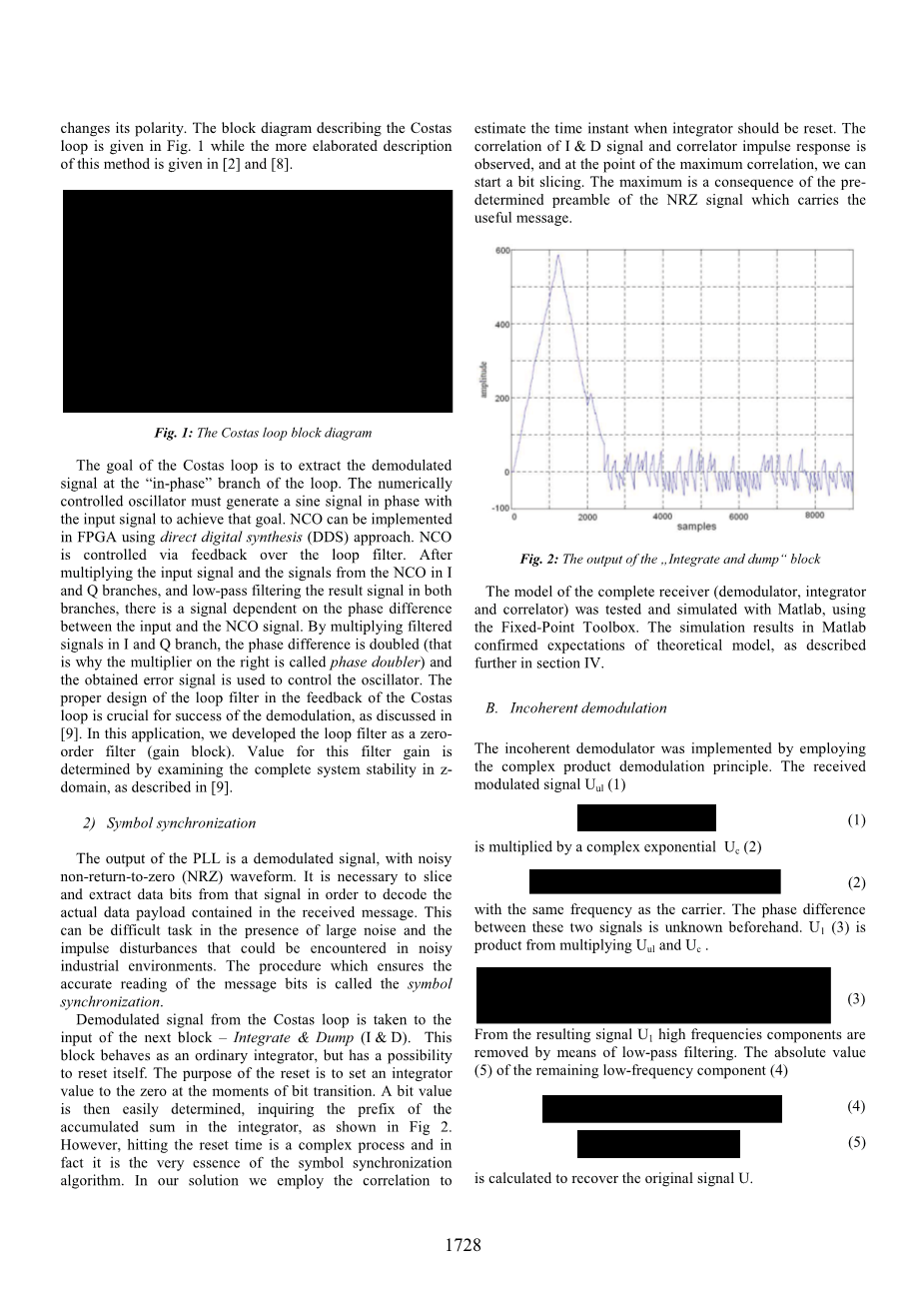
Costas环产生的解调信号被作为下一个模块的输出—整合和转储（I amp; D）。该模块的功能是作为一个普通的集成器，但是有可能重置其本身。复位的目的是在位过渡的时刻，设置一个积分值为零。如图2所示，在查询了集成器累积总和的前导代码后，信息位值很容易被确定。然后，设置击打复位的时间是一个复杂的过程，并且事实上，它也是码元同步算法的精髓之处。在我们的解决方案中，当集成器需要被重置时，我们采用相关性来估计这个瞬间的时间。我们观察了I amp; D信号和相关脉冲响应的相关性，并且在最大相关值处，我们可以开始进行一个位划分。这个最大值是在前文中定义了并且承载了有用信息的NRZ信号的结果。

采样点

幅值

图2 输出—整合和转储（I amp; D）的输出结果

完整的接收模块模型（解调器、积分器和相关器）在Matlab中利用不动点工具箱进行了试验和计算机仿真。Matlab产生的仿真结果证实了理论模型的预期结果，这一部分将在第四节进行更加详细的描述。

2.2 非相干解调

采用复解调原理实现了非相干解调。接收到的调制信号

(1)

被乘以一个复指数

(2)

有着和载波相同的频率。这两种信号的相位差事先并不知道。由和相乘得到

(3)

从上述结果信号我们可以看到，高频率部分通过低通滤波器后被滤除了。剩下低频信号部分（见公式4）的绝对值（见公式5）被计算，用来恢复原始信号U。

(4)

(5)

本文所描述的非相干解调器模型，在Matlab软件中进行了仿真。在位边界处，噪声表现形式为振荡的一些不必要传输误差，通过低通滤波器被发现和修正。仿真结果表明，第三阶低通滤波器足够实现本文目标。在信噪比大于5分贝的环境下，仿真模型的误码率小于0.1。由于使用二进制信号，非线性失真并不会对系统产生干扰，基于这个事实，为了简化硬件的实现，并没有采用平方根的方法。非相干解调器模型如图3所示。

平方根升余弦滤波器

低通滤波器

图3 复解调原理框图

用来保持该模型正常工作的曼彻斯特编码信号要尽可能的简单，特别是对于码元同步功能的实现。前导检测是通过使用相关的简单滤波器来实现的，这部分在第三章进行描述。载波信号的两个周期被用来传输一个数据位。

2.3 FPGA的实现

在目标硬件平台FPGA上，我们为相关解调和非相干解调接收机的实现开发了与之对应的VHDL模块，分别对应于图4和图5中的原理框图。这些模型适用于在Spartan 3A系列芯片上实现。入门工具板的核心是Xilinx XC3S700A集成电路。除了上述提出的FPGA芯片，还有三个模块也是实现完整接收机的必要组件：模数转化器（ADC）、数模转化器（DAC）和可编程增益放大器（PGA）。这些组件通过SPI总线接口连接到FPGA芯片。关于入门工具板“Spartan 3A开发套件”的更多详情可在文献[10]和[11]中了解到。

模拟

信号

数字

信号

Costas环

模数转换器

放大器

解调信号

最大值检测

综合器

位识别

相关滤波器

图4 相干解调接收器的原理框图

本文所提出的解调器设计在实际实现时的第一步，是要确保从接收到的调制信号中采集到合适的数据。A/D和D/A转换器，以及PGA增益模块的编程，都采用有限状态机的方式实现。由于ADC采用34位周期通信序列以及主时钟频率为50MHz，所以采样频率不能高于1.47MHz。

信息

逻辑转换器等

模拟

信号

解调

信号

移动平均滤波器

数字

信号

放大器

模数转换器

数控振荡器

图5 非相干解调接收器的原理框图

非相干解调过程中，通过几个模块获得ADC采样数据，如图3所示。至于创建I-Q信号，FPGA芯片的18*18乘法器和数控振荡器结合在一起使用，详细信息在文献[13]中有所描述。该组件使用内部RAM模块中存储的查找表，用来产生正弦信号和余弦信号。幅度分辨率设置为12位。离散正弦波形的质量由测量值为80dBc的无杂散动态范围（SFDR）来评价。使用第三阶低通滤波器过滤14位信号，以便消除混合图像。将I信号和Q信号平方相加后，使用移动平均滤波器来消除不必要的振荡。移动平均滤波器是被当作每个采样点都有一个加法器的移位寄存器来开发的。该移动平均滤波器输出的是15位解调信号。

为了从解调信号中恢复出原始信号，一些VHDL模块是十分必要的。例如，有限状态机是位同步的核心元件，逻辑转换器也通常被用来作为重构一个同步时钟的助力。在解调过程中，检测不同位之间的传输而不是相同位之间的传输（0-0和1-1之间发生）是十分重要的。这就是在转换检测被禁止的情况下，在利用有限状态机（FSM）的情况下实现的。这种状态需要持续超过一半的位时间，而又不到一整个位时间。并且这些转换都是由简单的推导逻辑来检测的，其中最后一个元素是前导检测模块（如图6所示）。它比较了内部存储的前导码和移位寄存器中的比特流，并且寻找最大值（伴随可调阈值），同时它还被当作相关过滤器。当控制逻辑检测到前导时，输出缓冲区被启用，否则它是处于高阻抗状态。

控制逻辑

移位寄存器

输出

输入

前导码

图6 非相干解调过程中的前导码探测器

至于相干解调，使用类似于非相干解调使用的VHDL模块，只是在严格要求的滤波器和NCO处有所差异。因此，本文直接采用文献[12]中的16位振幅分辨率的数字控制振荡器方法，并且它还提供120 dBc的SFDR。Costas环路中使用的滤波器采用第四阶。

4 结果

在本章节中，我们展示了BPSK相干解调和非相干解调程序的仿真结果。对于相干解调程序的仿真结果，首先必须要检查Costas环的稳定性。一个必须确保的关键点是，该Costas环可以保证数字控制振荡器在期望的工作频率中工作。对于第一阶Costas环，例如本文研究中所应用的，该工作频率被定义在固定频率的周围，并且不允许有太大的变化。我们通过一个错误信号的衰减循环来展示该Costas环的稳定状况（如图7所示）。在第二章A部分所描述的误差信号，是相位的倍频输出，并且输入到环路滤波器。我们可以从图7中看出，随着误差信号衰减到零，Costas环的稳定性状况。

幅值

采样点

图7 相位倍增输出的误差信号

作为BPSK信号在接收机输入的响应，在环路相位支路的位置提供一个解调信号作为输出。图8中给出了该解调信号的一个例子。如该图所示的光的振荡，在这里是由于两点原因：在传输信道中增加了噪声、在一个倍频载波频率的FIR滤波器上的成分组件是有限的。

采样点

幅值

图8 Costas环输出的BPSK解调信号

码元长度

码元长度

图9 相干解调过程中随着码元长度而变化的误码率

这些结果都是确认解调器正确工作的证据。在不同信噪比、位长、前导形状和载波频率条件下，对码元同步电路进行了测试。最后，一个综合结论在第五章得出。这个系统能够识别的发送信息长度长至100位，并且不破环其内部的同步性。此外，设置了一些相关参数后，信噪比小于-8分贝的调制信号是可能被恢复的。非相关解调的过程相较相干解调而言比较简单，因此，它需要较少的硬件资源。而利用较少的硬件资源也就意味着更低的功耗，这在硬件设计中往往是一个重要的考虑因素。非相干解调过程，可以恢复信噪比至少是5分贝的消息，所恢复消息的误码率在一个可接受的范围内（小于0.1）。在信噪比的计算函数中，误码率被作为符号长度中的一个固定参数。正如在第四章中前面讨论的那样，在BPSK通信系统中，符号长度对信息识别的精确度具有很大的影响。图9和图10分别展示了相干解调过程和非相干解调过程中，不同码元长度下的误码率计算结果。载波周期中每个符号的数量

剩余内容已隐藏，支付完成后下载完整资料

---

资料编号：[151841]，资料为PDF文档或Word文档，PDF文档可免费转换为Word