摘 要

细胞自动机的简单规则能够产生没有统计规律的复杂性表现，并以其并行性的特点，广泛应用于各个领域的模拟计算。而可逆性是细胞自动机的一个重要特征，其问题的研究有利于进一步的应用细胞自动机到各个领域。

本文利用一维细胞自动机的可逆性结论及特征矩阵的方法进行二维线性零边界扩展摩尔邻域细胞自动机的可逆性问题研究。并且同时还利用细胞自动机单射、满射与可逆性的关系去探讨了一类类似生命游戏规则的非线性细胞自动机的可逆性问题。基于上述的方法，本文发现了二维线性零边界扩展摩尔邻域细胞自动机的可逆性问题一个新的性质，并且得到了一些新的结论。

关键词：细胞自动机；可逆性；特征矩阵

Abstract

The simple rules of cellular automata can produce complex performance without statistics, and are widely used in simulation of various fields with its parallelism. Reversibility is an important feature of cellular automata, and its research is beneficial to further application of cellular automata to various fields.

In this paper, we study the reversibility of cellular automata in two-dimensional linear null-boundary extended Moore neighborhoods by using the reversibility conclusion of one-dimensional cellular automata and rule matrix method. At the same time, the problem of reversibility of nonlinear cellular automata similar to the rules of game of life is discussed by using the relationship between injective, surjective and reversible. Based on the above method, we find a new property of the reversibility problem of two - dimensional linear null - boundary extended Moore neighborhood cellular automata, and get some new conclusions.

Key Words: Cellular Automata; Reversibility; Rule Matrix

目 录

第1章 绪论 1

1.1 细胞自动机的历史 1

1.2 细胞自动机概述 1

1.3 细胞自动机可逆性的历史及其现状 3

1.4 本文的研究内容及章节安排 4

第2章 细胞自动机的理论基础 5

2.1 细胞自动机的定义 5

2.2 细胞自动机的相关性质 5

2.2.1 细胞自动机的分类 5

2.2.2 细胞自动机的边界条件 6

2.2.3 单射和满射及可逆性 6

2.3 一维细胞自动机可逆性问题的两种研究方法 6

2.3.1 De-bruijn图方法 6

2.3.2 特征矩阵方法 9

2.4 本章小结 11

第3章 二维细胞自动机的可逆性研究 12

3.1 理论知识 13

3.1.1 Laplace定理简介 13

3.1.2 相关性质的证明 13

3.2 相关结论的阐述与证明 21

3.2.1 整体不可逆情形 21

3.2.2 相等情形 22

3.2.3 块上矩阵情形 22

3.2.4 简答归纳情形 23

3.3 非线性细胞自动机的可逆性研究 24

3.4 本章小结 25

第4章 仿真与分析 26

4.1 算法设计与程序结构 26

4.1.1 算法设计 26

4.1.2 程序结构描述 26

4.2 分析与验证 27

4.2.1 结果验证 27

4.2.2 软件求解结果 28

4.3 本章小结 30

第5章 总结与展望 31

5.1 本文总结 31

5.2 展望 31

参考文献 32

致谢 33

第1章 绪论

1.1 细胞自动机的历史

细胞自动机，英文名Cellular Autumata,简称CA，也有文献译作元胞自动机，由John.Von.Neumam（冯.诺依曼）和Stanislaw M. Ulam于20世纪40年代末首次提出。冯.诺依曼在其在世时，证明了能够自我繁衍，进化的细胞自动机是存在的。Burks A W在其于1966年发表的论文中，总结了细胞自动机的成果，把细胞自动机介绍为一种可自我复制的模型，其具有可遗传性突变的特征^[1]。这种细胞自动机有数千个细胞，且每个细胞有29个状态，当时的计算机是无法模拟这种细胞自动机的，其存在仅是为了解决机器能否自我复制的数学问题。随后，在1970年，John Conway提出了命名为“生命游戏”（game of life）的一种细胞自动机。这种细胞自动机以其简单的规则及复杂的表象吸引了大批学者进行研究，并且随后证明了其具有图灵机计算等价性。在1983年，Stephen Wolfram对一维初等细胞自动机进行了研究，指出简单规则也会产生一定的复杂性^[2]。自80年代以后，细胞自动机在各个领域得到了广泛的研究^[3]。

1.2 细胞自动机概述

细胞自动机的基本元素是细胞，其分布在离散的欧几里德空间的网格上，所有细胞拥有共同的一个状态集，以离散的时间来进行所有细胞的状态更新。各个细胞的更新规则依据于其邻域细胞状态。

以一维初等细胞自动机为例，对于规则数73的初等细胞自动机来说，其规则图例为^[4]：

图1.1 规则73

对于如此规则的细胞自动机来说，当初始状态为只有一个细胞为黑色，其他都为白色，演化150步的图形如下：

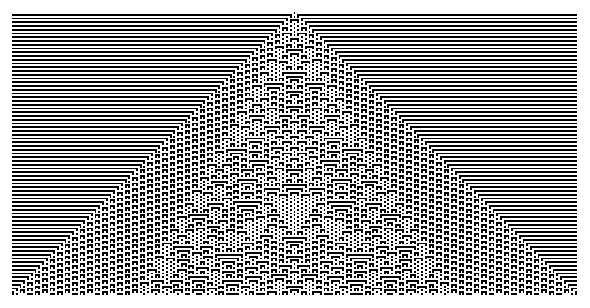
图1.2 规则73的演化图形