英语原文共 3 页，剩余内容已隐藏，支付完成后下载完整资料

ZnO量子点的时间分辨激子重组的温度和尺寸依赖性

I.Musa, F. Massuyeau, L. Cario,1 J. L. Duvail, S.Jobic,P.Deniard,

and E. Faulques1.

现今已经制备了不同尺寸的ZnO纳米晶体，并对其进行了表征。在低温下对他们的光致发光动力学进行了研究。对于最小的颗粒（3nm），缺陷诱导的长寿命光致发光发生在2.5eV附近，当样品温度T降低时，衰减时间长于3ns。从2.5eV带的热猝灭，缺陷中心处的激子离解能估计为约11.8meV。对于较大的微粒晶体（10到20nm），在3.32eV观察到的紫外发射在小于85ps内衰减并遵循Varshni定律[经由Varshni公式所拟合出的Y，P物质（阿姆斯特丹）34，149（1967年）]。

ZnO是一种宽禁带N型半导体适合用于制备器件和紫外（UV）激光器，其在室温（RT）下和在UV和可见光范围内表现出两种强的光致发光（PL）结构。在3.30eV（375nm）的第一个UV发射通常归因于近带边（NBE）自由激子的主要贡献。绿色光谱范围（以下称为G带）的更广泛的ZnO发射发生在2.2-2.5eV（480-560nm）之间，并且总是反映存在于ZnO结构中的各种类型的本征缺陷，尤其发生在量子点（QD）和纳米晶体中。

ZnO量子点的吸收和荧光研究有详细记录，而有关样品温度，尺寸和固有缺陷对ZnO纳米结构中NBE（近带边）和G（绿色光谱）带的量子限制效应和激子衰变动力学的综合影响的报道较少。在这篇文本中，我们研究了这些由软化学途径产生的不同控制尺寸（3-20nm）的合成原始ZnO纳米晶体的性质，通过透射电子显微镜（TEM）图像和x射线衍射Rietveld改进显示图像，我们对ZnO纳米颗粒的合成分别得到3，5,10,20nm和4.5,5,10.5,24.2nm的表观尺寸。纳米颗粒有一个结构特点，六边形的纤锌矿结构型。

我们期望我们最小的尺寸为3nm的半径小于主体ZnO玻尔半径（aB = 2.34nm）[参考文献10]的纳米颗粒可以具有相对高的激子能量，并且电荷载流子处于强约束状态。相比之下，半径大于ZnO波尔半径的量子点中的激子能量相对较小，这些量子点中的载流子处于弱量子限制状态。因此，在目前的研究工作中，我们的尺寸5nm和尺寸10-20nm的ZnO纳米颗粒应当分别处于中间态和弱约束状态。图1显示出了描绘激子的最低激发态的能量的光吸收边朝向高能量移动，由于zno晶体量子点粒径的尺寸减小。可以通过将最低激发态的能量表示为纳米晶体半径R的函数来再现该趋势。

;

其中ε₀和ε 是自由空间和粒子的介电常数，e为基本电荷，和mu;是电子的有效减少质量，这个最佳拟合方程，在实验中吸收边缘能量获得的me=0.24，mh=0.45，和, ε= 3.7与以melt;mh为特征的中间限制状态很好地一致。该曲线在溶液中产生4,6,7和14nm的量子点平均粒径。 可以看出，E几乎饱和，同时延伸到尺寸上限，另外使用具有在325nm（3.81eV）的共振激发的稳态PL（光致发光光谱）研究颗粒。观察到强的UV峰，随着尺寸增加逐渐红移（图1（a），下曲线），对于3,5,10和20nm直径分别位于3.406,3.342,3.263和3.179eV处，该PL带已经被分解成几个构成带，其来自受体结合的AX激子，施主的DX激子（在3.25eV）和游离的X激子，量子点限制效应通过从20nm到3nm大小增加约100meV斯托克斯位移来证实。

图1 （在线颜色）（a）ZnO纳米晶体各种平均直径在室温下的光吸收和稳态的（光致发光光谱）PL：最低激发态和PL最大对半径的相关性。 菱形和圆形对应于光吸收边（箭头）和PL最大值（激发，lambda;exc = 325nm）。（b）用于ZnO纳米颗粒的时间分辨PL光谱（RT，lambda;exc = 267nm），超过1ns。 插图：G和UV带的瞬态PL强度比随尺寸的变化。

正如我们以前的研究，为了看到大小，缺陷和低温对激子动力学的影响，我们使用飞秒激光和条纹相机系统，进行了时间分辨PL实验。图1（b）显示了对于不同尺寸在1ns的时间上积分的室温瞬态PL光谱. 所有纳米颗粒显示两个不同的瞬态发射带, UV峰值匹配良好，共振激发的ZnO近带边稳态发射约3.10-3.3eV，伴随着约2.98eV的较小未分辨带，以及在光谱的蓝 - 绿区域中的宽发射G带，其归因于类似于稳态PL情况的本征点缺陷。还存在瞬态UV峰的蓝移从3.10eV至3.35eV（E = 0.25eV）, 结果如 图1（a）和1（b）可以通过量子限制自然地解释，其将导带和价带的能级移开，导致当纳米颗粒尺寸减小时跃迁能量发生蓝移。

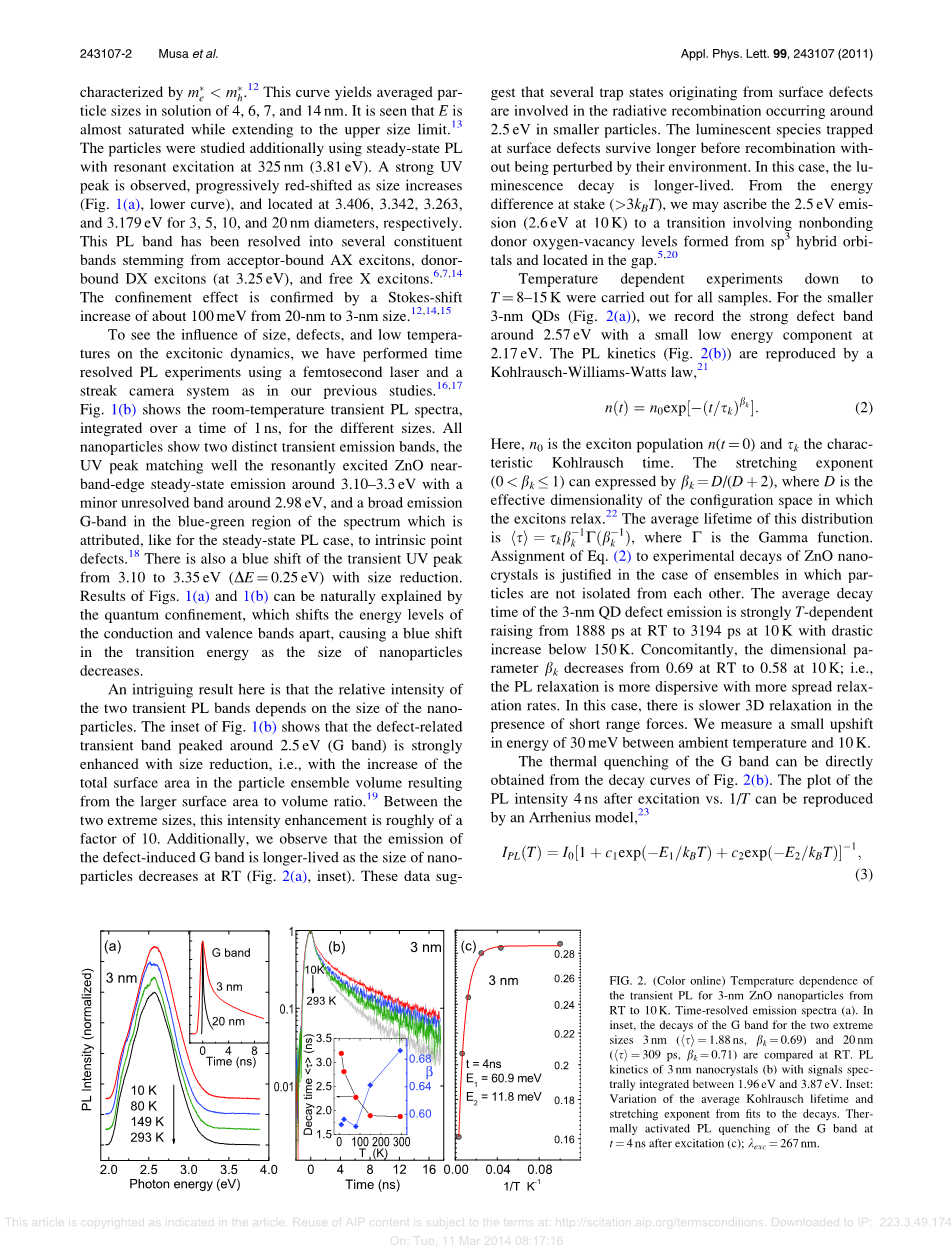
这里的一个有趣的结果是，两个瞬态PL频带的相对强度取决于纳米粒子的尺寸大小。随着由更大的表面积与体积比率所导致的颗粒集合体积中的总表面积的增加，图1的插图。 图1（b）表示在2.5eV（G带）附近峰值的缺陷关联的瞬态带在尺寸减小时强烈增强。在两种极端尺寸之间，这种强度增强大致为10倍。此外，我们观察到缺陷诱导的G带的发射更长，因为在RT下纳米颗粒的尺寸减小（图2（a） ，插图）。这些数据表明，几个陷阱态起源于发生在约2.5 eV的小颗粒的表面缺陷参与的辐射复合。被困在表面缺陷的发光物质在重组之前存活更长时间，而不被其环境干扰，在这种情况下，发光衰减寿命更长。 从所关注的能量差（gt; 3kBT），我们可以将2.5eV发射（在10K下2.6eV）归因于涉及由sp混合轨道形成并位于间隙中的非结合供体氧空位水平的跃迁。对所有样品进行温度依赖性实验从T= 8–15k，对于较小的3 nm量子点（图2（a）），我们记录了2.57 eV左右的强缺陷带，在2.17 eV具有小的低能量分量。光致发光动力学（图2（b））是由一个可用威廉姆斯瓦法复制再现。

这里，n0是激子群体n（t=0），tau;k是特征Kohlrausch（科尔劳施）时间。拉伸指数（0 lt;beta;k lt;=alpha;1）可以由beta;k = D /（D 2）表示，其中D是其中激子弛豫的配置空间的有效维度。这种分布的平均寿命是其中Gamma;是伽马函数。方程的分配Eq（2）对ZnO纳米晶体的实验衰变在其中颗粒彼此不分离的集合体的情况下是合理的，3-nm 量子点缺陷发射的平均衰变时间是强T依赖性的从RT的1888ps升高到10K的3194ps，急剧增加到150K以下。同时，尺寸参数beta;k从RT下的0.69降低到10K时的0.58；L松弛更具有分散性，具有更多的分散松弛率。在这种情况下，在存在短程力的情况下存在较慢的3D松弛。 我们测量在环境温度和10K之间的30meV的小的升档。G带的热淬火可以是直接的从图1的衰减曲线获得图 2（b），激发后4ns的PL强度对1 / T的曲线可以通过Arrhenius（阿伦尼乌斯模型）模型再现。

图 2.（在线颜色）3纳米ZnO纳米颗粒的瞬态PLRT至10K温度依赖性，时间分辨发射光谱（a），在插图中，G带的衰减为两个极端在RT下比较尺寸3nm（tau;= 1.88ns，beta;k= 0.69）,具有在1.96eV和3.87eV之间光谱积分的信号的3nm纳米晶体（b）的PL动力学.插入：平均Kohlrausch寿命和拉伸指数从拟合到衰变的变化，热激活的PL淬火的G带激发后t =4ns（c）; ，lambda;exc = 267nm。

图3（颜色线）ZnO纳米颗粒从RT到8K的瞬态PL的温度依赖性。NBE的激子对T为10 nm和20 nm ZnO量子点时间分辨发射光谱。a: 接近设备功能的对应时间信号（交叉）,b: 寿命lt;85ps。 插图：NBE发射作为T的函数对于10nm和20nm ZnO纳米晶体的能量，由Varshni定律在“T²”

其中I₀是在T = 0K，c1，c2参数下的峰强度，kB是波尔兹曼常数。对数据的拟合产生E₁ = 60.9 10.5meV，接近于块状ZnO中的自由激子结合能，与捕获在缺陷处的激子的解离能E₂ = 11.8 1.2meV对应（图2c）。然后可能的是，3nm QD发射由缺陷处的复合控制，来自具有约60meV的激活能的NBE激子部分的较小贡献（见图1b，黑色线）。

在10 nm和20 nm QDs的情况下（图3），NBE激子发射被红移，并且PL强度也随着温度增加而被热淬火。这些样品中PL发射的最大值符合Varshni定律。

E_PL(T)=E₀- alpha;T²

beta; T

其中E₀ = 3.167eV（20nm）和3.185eV（10nm）0K时的跃迁能alpha; = 14times;10 ^-4（20nm）和11.3times;10 ^-4 eV K ^-1（10nm），beta; = 920K（图3b）。我们还可以获得在低T的数据的更好的拟合与修改的Varshni定律，其中alpha;T²-- alpha;T⁴和beta; T—beta; T³。拟合和实验点之间的差异小于14K以下的3meV，这是自由激子的典型而不是局部激子。这些NBE激子的寿命太短（lt;85ps），以观察随温度的时间依赖性。

总之，我们研究了不同尺寸的ZnO量子点的温度依赖性时间分辨PL实验。我们已经证明了与UV区域中的限制激子和绿色光谱范围中的缺陷相关的两个主要发射的不同激子动力学。当QD尺寸增大时，前者的超短寿命UV带移动到更高的能量，这次发射是在较低的温度下，它主要来源于自由激子Varshni定律。暂时归因于点表面处的氧空位的后者PL带显示具有约11.8meV的激子解离能的长寿命衰变。

参考文献：

[1]M. H. Huang, S. Mao, H. Feick, H. Yan, Y. Wu, H. Kind, E. Weber, R.Russo, and P. Yang, Science 292, 1897 (2001).

[2]J. S. Bendall, G. Visimberga, M. Szachowicz, N. O. V. Plank, S. Romanov,C. M. Sotomayor-Torres, and M. E. Welland, J. Mater. Chem. 18,

5259 (2008).

[3]K. Borgohain and S. Mahamuni, Semicond. Sci. Technol. 13, 1154 (2008).

[4]D. Bera, L. Qian, S. Sabui, S. Santra, and P.-H. Holloway, Opt. Mater. 30,1233 (2008).

[5]A. Janotti and C. G. Van de Walle, Rep. Prog. Phys.72,126501(2009).

[6]V. A. Fonoberov, K. A. Alim, A. A. Balandin, F. Xiu, and J. Liu, Phys.Rev. B 73, 165317 (2006).

[7]L. Beacute;aur, T. Bretagnon, B. Gil, A. Kavokin, T. Guillet, C. Brimont, D.Tainoff, M. Teisseire, and J.-M. Chauveau, Phys. Rev. B 84, 165312(2011).

[8]V. Noack and A. Eychmuuml;ller, Chem. Mater. 14, 1411 (2002).

[9]N. Uekawa, N. Mochizuki, J. Kajiwara, F. Mori, Y. J. Wu, and K. Kakegawa,Phys. Chem. Chem. Phys. 5, 929 (2003).

[10]R. T. Senger and K. K. Bajaj, Phys. Rev. B 68, 045313 (2003).

[11]L. E. J. Brus, Chem. Phys. 80, 4403 (1984).

[12]K.-F. Lin, H.-M. Cheng, H.-C. Hsu, L.-J. Lin, and W. F. Hsieh, Chem.Phys. Lett. 409, 208 (2005).

[13]J. C. Nie, J. Y. Yang, Y. Piao, H. Li, Y. Sun, Q. M. Xue, C. M. Xiong, R.F. Dou, and Q. Y. Tu, Appl. Phys. Lett. 93, 173104 (2008).

[14]G. Kiliani, R. Schneider, D. Litvinov, D. Gerthsen, M. Fonin, U. Ruuml;diger,A. Leitenstorfer, and R. Bratschitsch, Opt. Express 19, 1641 (2011).

[15]In this work, we define the Stokes shift as the energy difference between the absorption maximum (different from the absorption edge energy) and the maximum of the steady-state photolumin

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[25638]，资料为PDF文档或Word文档，PDF文档可免费转换为Word