外电场对硼烯光电性质的影响毕业论文
2020-02-15 09:04:08
摘 要
硼烯作为硼元素的一种同素异形体,是备受当今科学界关注的一种新型二维材料。硼烯并非自然存在,仅能依靠人工制备,因此关于硼烯的探究也多在理论研究以及模拟仿真上。虽实际制备较为困难,但硼烯优异的光电特性却备受研究人员的青睐,在新型材料市场上具备极大的潜力。
本文以第一性原理作为理论基础,并借助了材料计算软件Materials Studio来完成对硼烯模型的建立。通过软件中的CASTEP模块完成对硼烯模型的几何优化,后同样通过CASTEP模块计算本征硼烯的能带结构和各光学参数(反射率、折射率、吸收率、介电函数等)来探究硼烯的光电特性。之后从中引入外电场,并计算出外电场下硼烯的能带结构和各光学参数。最后将本征硼烯和外电场下的硼烯各参数进行比较讨论,从而得出外电场对硼烯光电性质的影响。
关键词:硼烯;二维材料;第一性原理;光电性质
Abstract
Borophene is an allotrope of boron. It is a new type of two-dimensional material that has attracted much attention from the scientific community. Borophene does not exist naturally and can only be prepared artificially. Therefore, the research of Borophene is mainly on theoretical research and simulation. Although the actual preparation is difficult, the excellent photoelectric properties of Borophene are favored by researchers, and Borophene have great potential in the market of materials.
This paper is based on the first principle. The model of Borophene is built in Materials Studio. The model was optimized by CASTEP module. And the energy band structure and optical parameters (reflectivity, refractive index, absorptivity, dielectric function) of Borophene are calculated by CASTEP module to explore the photoelectric properties. Then we add external electric field in CASTEP, and calculate the energy band structure and optical parameters of Borophene. Finally, the parameters of Borophene in the external electric field are compared and discussed with parameters of Borophene, and get the effect of external electric field on the photoelectric properties of Borophene.
Key Words:Borophene; Two-dimensional material; First principles; Photoelectric property
目 录
第1章 绪论 1
1.1 引言 1
1.2 硼烯的结构 1
1.3 硼烯的性质 2
1.3.1 导电性质 2
1.3.2 光电性质 3
1.4 硼烯的应用 3
1.4.1 超级电容 3
1.4.2 储氢 3
1.4.3 电池的电极材料 3
1.5 本文主要研究内容 3
第2章 计算理论方法 5
2.1 第一性原理 5
2.2 密度泛函理论 5
2.2.1 Hohenberg-Kohn定理 5
2.2.2 Kohn-Sham定理 6
2.2.3 交换关联能泛函 7
2.3 光学性质计算 7
2.4 Materials studio软件 8
第3章 硼烯的模型建立 10
3.1 硼烯模型 10
3.2 硼烯模型优化 11
第4章 本征硼烯计算 13
4.1 计算设置 13
4.2 本征硼烯计算结果 15
4.2.1 能带结构 15
4.2.2 反射率 15
4.2.3 吸收率 16
4.2.4 折射率 17
4.2.5 介电函数 18
第5章 外电场下的硼烯计算 19
5.1 外电场下的计算设置 19
5.2 外电场下的硼烯参数 19
5.2.1 电场强度为1.0eV/Aring;/e时 19
5.2.2 电场强度为2.0eV/Aring;/e时 22
5.2 各外电场下的参数对比 25
第6章 结果与讨论 28
参考文献 29
致 谢 30
第1章 绪论
1.1 引言
自石墨烯发现以来,其优异的特性就掀起了科研人员们对于二维材料的探究热潮。而在元素周期表中,硼碳虽彼此相邻,但硼烯与石墨烯有诸多不同。首先,石墨烯在自然界中就天然存在,可以从石墨晶体上剥离获取,但硼烯在自然界中并非天然存在,仅能通过人工制备。从结构上看,硼比碳相比最外围少了一个电子,并且硼同素异形体种类多且冗杂,故制备二维硼烯相对困难。因此科研人员对硼烯的理论结构虽探究已久,但却从未在现实中制备。而硼烯的制备也成为了材料物理界的重大热点。
2016年,吴克辉团队在Nature Chemistry发表了关于硼烯制备的最新研究成果。吴克辉团队采用了超高真空分子束外延直接进行单原子层构筑的方式,成功在Ag衬底中制备出硼烯。此次重大探究实验中,共发现了两种硼烯结构,符合了先前所提出的具有不同周期孔的三角形晶体结构。更重要的是,制备出来的硼烯表现出了良好的抗氧化性,表明硼烯将来在各材料器件的应用中具有很大的潜力。
硼烯的成功制备是凝聚态物理的重大突破,为硼烯的实际研究提供了很大便利。硼烯在多年的理论探究下,已经发现了很多重要的特性。比如硼烯具有金属特性,具备多样化电子性质,并且根据设想,硼烯甚至可能表现出超导特性,是极佳的光电材料。此外硼烯的抗氧化性,有效防止了二维材料的容易受氧化所影响的缺陷。同时因为硼烯具有键长比较短的特性,故在机械性能方面表现优异。硼烯的杰出的抗氧化性、机械性能和导电性等特点,都突显出了硼烯材料运用于当今各器件的巨大潜力。
本文将会通过Materials Studio软件来计算探究外电场对硼烯光电性质的影响。在外电场的作用会使石墨烯的光电性质产生改变,而硼烯也可能同样存在其特性,即外电场的变化会引发其光电性质的变化,如能带结构和介电函数、吸收系数、折射率、反射率等参数的变化。探讨此现象也可以让我们更好的了解到硼烯对于集成电路、光电器件的应用。
1.2 硼烯的结构
因在周期表中相邻,硼与碳拥有了相似的机械性质和硬度,类似碳的sp2杂化轨道,因为具有共价键半径短以及多样的价态特点,所以相对容易在低维度下形成同素异形体。作为二维硼材料,硼烯主要分为三角形、六边形以及三角形和六边形的混合结构。具体结构如图1所示[1]。科研人员因受到近年石墨烯热点的启发,故针对硼烯便首先提出了与石墨烯相似的六角形平面结构。后通过第一性原理进行优化,六边形硼烯结构在水平方向上出现了扭曲现象,虽然从结构上看,硼原子还处在一个平面内,但因为扭曲现象造成了该硼烯结构并不稳定。通过稳定性的考虑,三角形硼烯结构被科研人员提出。与六边形硼烯不同,三角形硼烯在结构中心比六边形硼烯多了一个硼原子,并且原子分布到了两个层面上,呈现出了褶皱形状。以上两种模型多存在于理论情况下,因为受实际影响,要让硼烯完全由以上两种结构之一构成是不现实的,所以科研人员发布了新的硼烯模型,即由三角形硼烯和六边形硼烯混合形成,比如alpha;硼烯层和beta;硼烯层。经过理论探究,其第三种结构表现出的稳定性最优良。
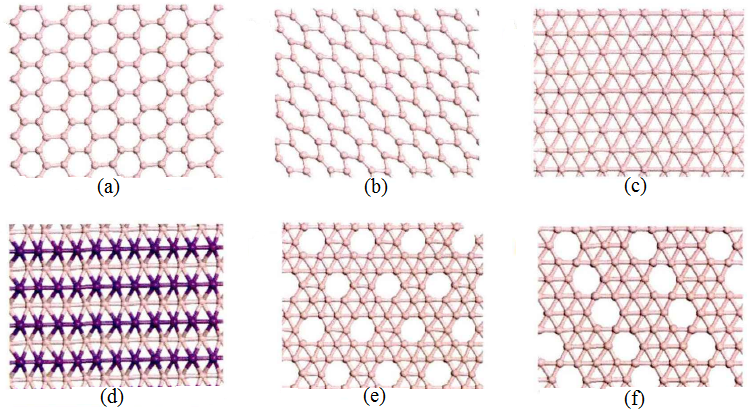
图1.1 (a)六边形硼烯结构;(b)优化后的六边形硼烯结构;(c)三角形硼烯结构;(d)优化后的三角形硼烯结构;(e)alpha;硼烯层结构;(f)beta;硼烯层结构
1.3 硼烯的性质
1.3.1 导电性质
硼烯拥有极高的导电率,并呈现出金属特性。根据Bezugly等人将硼烯纳米管与石墨烯纳米管的I-U曲线进行对比探究,发现硼烯纳米管的电子输运通道更多,表明硼烯电子传输性质要优于石墨烯[2]。硼烯因为存在两层式结构即有褶皱,所以表现出了各向异性导电特性,同时硼烯还存在因为水平拉伸导致发生垂直方向膨胀的“负泊松比”现象。以上种种特性都表明了硼烯导电性能极佳,可以作为十分理想的电极材料。
1.3.2 光电性质
翟天佑等人的研究表明,硼烯具有高电导增益(465A·W-1)、高量子效率(1.78times;105%)、高比探测率(4.91times;1011Jones),并且硼烯具有低开启电场(3.60V/mu;m)、低阈值电场(5.08V/mu;m)、高场增强因子(1363)和高电流密度(5.80V/mu;m下为7.47mA·cm-2)[3]。这些结果表面了硼烯具备高的光敏感性,拥有快速、可逆并且稳定的光响应以及优异的场发射性质,其优异的光电性质也使得硼烯纳米材料在当今光电器件的应用上具备十分强大的潜力。
1.4 硼烯的应用
1.4.1 超级电容
超级电容能够以极高的效率完成充电放电,同时使用寿命极长,功率密度远高于一般的电池,能够在电车、电轨的运用中起到重大作用。经长年科研发现,硼烯因为其优异的导电特性,以及具备的超导特性[4],非常适合用做超级电容的材料。
1.4.2 储氢
探究发现,硼烯能够储存大于自身质量百分之十五的氢,具备极佳的储氢性能,同时硼烯能将水分解成氢氧离子,即能作为催化剂来使用。而且硼烯很容易将氢原子吸附到自身结构中,强大的储氢以及吸附性能,使得硼烯成为一种很有前景的储氢材料。
1.4.3 电池的电极材料
电池是以化学能的形式储存能量,具备高能量转换率,高储存效率等优点。而电极材料通常由导电性能优良的材料构成。
硼烯的优良导电性质,以及罕见的“负泊松比”现象,使硼烯能作为一种非常优秀的电池电极材料。更重要的,二维硼可以根据原子排列的位置不同,而形成表现出不同的特性的物质,比如即能生成高导电性亦或是高硬度的硼氧化物。同时硼烯轻质量、高表面活性都表明了硼烯作为导电材料的优异前景。
1.5 本文主要研究内容
本次实验设计以第一性原理为理论基础,通过材料计算软件Materials Studio来完成对硼烯的建模并完成结构优化,计算硼烯的光学性质参数,如能带结构和介电系数、吸收系数、折射率、反射率等,并在模型中添加外电场,以此探讨外电场对硼烯光电性质的影响。
本文主要介绍了硼烯的研究背景、原子结构、光电性质以及应用前景,第一性原理的理论方法,Materials Studio软件简介,硼烯模型的构建优化,硼烯模型的光学参数计算,以及在外电场下硼烯光学参数的变化,并最终探讨出外电场对硼烯光电性质的影响结果。
第2章 计算理论方法
2.1 第一性原理
现今材料计算科学技术中的模拟计算主要有如下两个方向:一是以分子力学为基础的经验计算,二是以量子理论为基础的理论计算[5]。在探究热力学性质时,一般都采用分子力学的经验计算方法。在研究带有波粒二象性的粒子时,便通常采用量子力学理论来计算,而量子理论的计算便是从第一性原理发起的。
第一性原理即以原子核和电子的相互作用以及运动规律为基准,通过量子理论并结合近似计算法,来得出薛定谔方程。与分子力学不同的经验计算不同,第一性原理计算并不需要经验参数,只需分子积分即可[6]。第一性原理计算方法包含了从头计算法和密度泛函理论。其中从头计算法得出体系各参数主要通过波函数来表示,与从头计算不同,密度泛函理论则是通过电子密度来表示。而本次关于硼烯的性质计算主要以密度泛函理论为理论基础。
2.2 密度泛函理论
密度泛函理论是以量子力学为理论基础的,基本用于材料物理中电子结构的运算。原先从头计算法是以波函数来表示系统体系参数,但在部分情况使用不便,所以Hohenberg、Kohn与Sham提出了以电子密度代替波函数作为基本量,以此来明确非均匀相互作用。
2.2.1 Hohenberg-Kohn定理
由Hohenberg、Kohn表明了密度泛函基本准则:在系统体系的计算中,用电子密度来作为整个体系的基本参量。并提出了相关定理两则:定理一,当不用考虑电子自旋的影响的情况下,对于费米子系统,整个系统基态的能量是这个体系电子密度的唯一的泛函;定理二,粒子数固定时,能量泛函E(rho;)为准确粒子数密度函数rho;(r)取极小值,同时和基态能量相等[7]。
由上述两则定理可总结得如下公式:
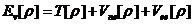 (2.1)
(2.1)
公式中T[rho;]表示电子密度对与动能函数,Vne[rho;]表示对于原子核引力能函数、Vee[rho;]表示电子之间相互作用能函数。
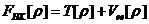 (2.2)
(2.2)
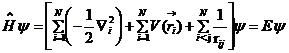 (2.3)
(2.3)
采用变分法的数学变化以后,得出以下三个式子:
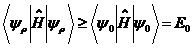 (2.4)
(2.4)
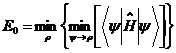 (2.5)
(2.5)
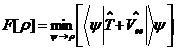 (2.6)
(2.6)
2.2.2 Kohn-Sham定理
上节所述定理虽构建了密度泛函理论的核心架构,但在实际多粒子体系的运用中往往还需要进行近似计算才能解决问题。为此,Kohn、Sham提出了Kohn-Sham 方程。将Hohenberg-Kohn定理的T、V已知部分进行了取舍整理[8],同时将各式子重新整合,最终得出以下式子:
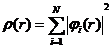 (2.7)
(2.7)
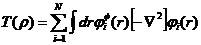 (2.8)
(2.8)
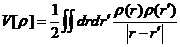 (2.9)
(2.9)
同时将T[rho;]、T0[rho;]相差部分带入Exc[rho;],带入能量泛函表达式后,式子如下所示:
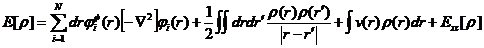 (2.10)
(2.10)
式中,Exc[rho;]表示交换关联势。
后由泛函变分得出Kohn-Sham方程:
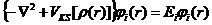 (2.11)
(2.11)
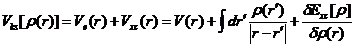 (2.12)
(2.12)
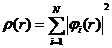 (2.13)
(2.13)
式子(2.11)、(2.12)、(2.13)即为Kohn-Sham方程,通过该方程组,有相互作用的电子体系的动能可以由无相互作用的电子体系动能表示,而T[rho;]同To [rho;]的差值部分代入交换关联式 Exc[rho;]中,便能够让电子、原子存在相互作用的体系转换为无相互作用情形下的粒子方程。
2.2.3 交换关联能泛函
关于密度泛函理论的计算,需要对泛函进行近似处理才能进行计算。泛函的近似处理常规采用局域密度近似(LDA)和广义梯度近似(GGA)。
局域密度近似是通过电子密度函数rho;(r)求得非均匀电子气的交换关联泛函[9]。该近似处理是由Kohn和Sham提出的,其表达式如下所示:
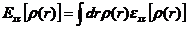 (2.14)
(2.14)
分析可知,局域密度近似的局限性在于rho;(r)的变化幅度,若其变化幅度大,则计算精度会大大下降。仅有当变化范围相对较小,才能保证计算的准确性。因此,系统中的电子密度变化是局域密度近似的关键,从而在许多体系中有诸多限制。
对此,Perdew等人提出了广义梯度近似。广义梯度近似对局域密度近似对于电子密度的限制缺陷进行了优化调整,兼顾到了电荷密度与交换关联能间的关系,其表达式为:
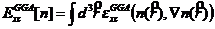 (2.15)
(2.15)
经上分析,广义梯度近似对于实际中的系统体系计算更加适用,并且伴随着一路以来的科学探索,科学人员提出了许多关于广义梯度近似泛函,如PBE、PRBE、PW91等。本次关于硼烯模型计算运用的即为PBE泛函,即GGA-PBE。




