快速傅里叶变换(FFT)算法的FPGA仿真实现毕业论文
2020-02-17 22:34:28
摘 要
本文研究了一种在FPGA上实现32点FFT变换的通用方法。使用核心为复数乘法器的设计来架构FFT算法中的radix-2蝶形单元,溢出控制单元以及地址和逻辑控制模块。用Modelsim软件进行FFT模块的前后仿真; Matlab编写了Matlab仿真结果与FFT函数结果的比较程序,验证了仿真结果的正确性[[1]]。所得结果对于数字频谱分析领域具有重要的指导意义。
论文主要研究了快速傅里叶变换(FFT)的仿真实现。它是对时域和频域转换的基础算法,而 FPGA是内部结构规则简单,容纳许多相同算术单元的元件,适合用来实现FFT算法。
研究结果表明:所设计的系统能够有效地完成整体设计要求,同时保证操作的准确性和复杂性。即FFT运算结构相对简单且固定,适用于FPGA的硬件实现,可以平衡速度和灵活性[[2]]。
本文的特色:基于FPGA双端口RAM;采用radix-2时域提取,顺序输入和逆序输出的方法。
关键词:FPGA;FFT;IP核;基2
Abstract
In this paper, a general method of 32-point FFT transform on FPGA is studied. The radix-2 butterfly unit, overflow control unit and address and logic control module of FFT algorithm are constructed by using complex multiplier as the core. Modelsim software is used to simulate the FFT module before and after the simulation, and MATLAB compiles the comparison program between the simulation results of MATLAB and the results of FFT function, which verifies the correctness of the simulation results. The results obtained have important guiding significance in the field of digital spectrum analysis.
This paper mainly studies the simulation implementation of Fast Fourier Transform (FFT). It is the basic algorithm for time-domain and frequency-domain conversion. The internal structure of the FPGA is simple and contains many elements of the same arithmetic unit. It is suitable for FFT algorithm.
The results show that the designed system can effectively fulfill the overall design requirements, while ensuring the accuracy and complexity of the operation. That is, FFT operation structure is relatively simple and fixed, suitable for hardware implementation of FPGA, and can balance speed and flexibility.
The features of this paper are: dual-port RAM based on FPGA, radix-2 time domain extraction, sequential input and reverse output.
Key Words:FPGA;FFT;IP core;Base 2
目录
第1章 绪论 1
第2章 FFT算法和FPGA基础知识 2
2.1 FFT算法简介 2
2.1.1 radix-2FFT算法简介 2
2.1.2 radix-2FFT算法基本原理 3
2.1 FPGA的简介 8
2.2.1 FPGA的结构及其设计原则 8
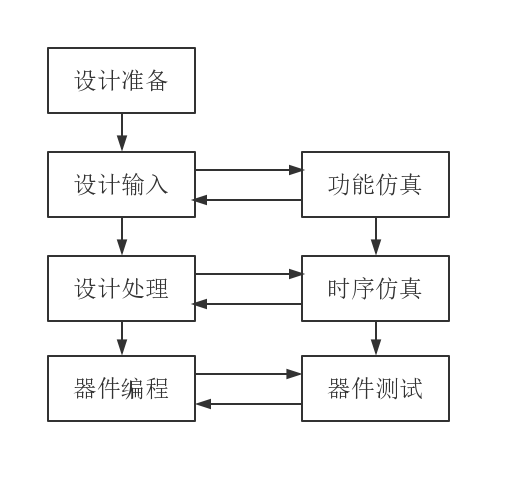
2.2.2 开发流程和开发软件简介 9
2.2.3 IP的基本特征 10
第3章 FFT处理器的FPGA的实现 12
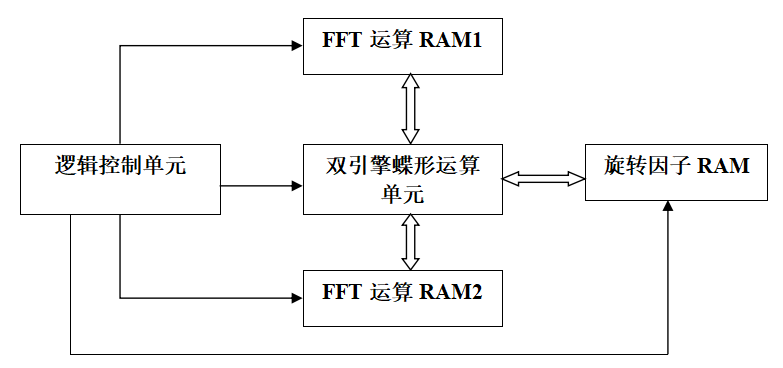
3.1 整体设计 12
3.2 FFT处理器的工作过程 12
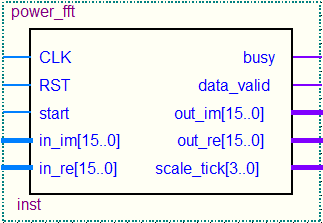
3.3 引脚说明 13
3.4 存储单元 14
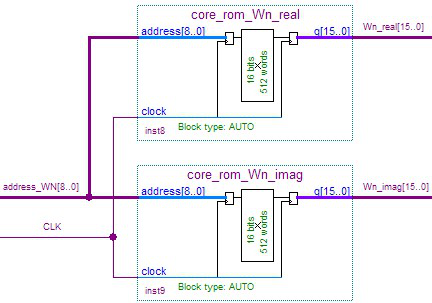
3.5 旋转因子单元 14
3.6 蝶形运算单元 15
3.7 逻辑控制单元 17
第4章 FFT系统仿真测试 18
4.1 FPGA前端设计 18
4.1.1 算法验证和RTL设计 18
4.1.2 仿真与综合 18
4.1.3 静态时序分析 19
4.2 FFT处理器的资源利用情况 20
4.3仿真过程及结果分析 22
4.3.1 实线性信号的仿真 22
4.3.2 实单频正弦信号的仿真 24
4.3.3 复单频正弦信号的仿真 26
第5章 结论 28
参考文献 29
致谢 30
第1章 绪论
快速傅里叶变换(FFT)多在信号的变换处理时使用,是对离散傅里叶变换(DFT)进行变换得到的。DFT从频域对信号系统进行分析,但其存在的问题是随着序列长度的增加,会呈非线性的极大增加计算量。幸运的是,在1965年,Cooley和Turkey研究出了一种新的方法计算DFT,这就是快速傅立叶变换的初现[[3]]。从本质上说,FFT是另一种基于DFT的计算方式的转变,使用一个快速,高效的方法来减少DFT的计算复杂度。同时,FFT也使得DFT获得更为广泛的应用,提升了DFT的价值。此外,高度的耦合的FPGA具有的高并行特性加之FFT高度规则的运算结构使得在FPGA上实现FFT的有效方式。作为之前可编程器件的替代,FPGA内含高速数字信号处理(DSP)装置和高吞吐的快速RAM模块[[4]]。所以使用FPGA成为了一种更便捷的方法,避免了软件方法带来的速度的限制,缩短开发实现FFT处理的成本和周期,是进行FFT算法的理想环境。FPGA以高性能、高灵活性、友好的开发环境、在线可编程等特点使得基于FPGA的设计能满足实时数字信号处理的要求[[5]]。
作为专用集成电路(ASIC)中一类,在对传统逻辑电路和门阵列PAL、GAL、CPLD等的不断使用和研究后,其结晶FPGA(Field-Programmable Gate Array)出现了。FPGA增加了内部可用的设计空间,又改进之前可编程器件门电路数偏少的问题。FPGA内部规则简单,结构通常可以设计很多相同的运算单元。也就是说,FPGA指定方向运算时,可以提升至通用的DSP芯片数十倍的速度。相对而言,FFT运算构成可以说是简单的复制结构,FPGA很合适进行FFT的仿真,对速度和灵活性也有优势,而传统的DSP实现的话会有太多浪费。而且FFT算法里有很多的乘法运算,这恰恰是DSP芯片设计时缺少的。会浪费许多DSP芯片来完成所要求的信号处理方案,会因此增加能源功耗、提高价格和体积[[6]]。FPGA芯片内部设计有多个乘法器内核,就不会有使用DSP芯片时的问题。近年来,FPGA作为可编程元件,相关的技术和运用越加丰富,且其集成度、速度不断提高,被选用进行相关算法实现就更为广泛。
本论文就是在这样一个背景下提出一种基于FPGA的32点基-2FFT算法的具体实现方法。
第2章 FFT算法和FPGA基础知识
2.1 FFT算法简介
离散傅立叶转换(Discrete Fourier Transform, DFT)过去常用于数位讯号处理或通讯系统,但其运算复杂度为 O ( N2) ,它会随着运算点数增加而变的相当复杂。因此,1965 年 Cooley-Tukey 提出 FFT 算法,其运算复杂度降为 O( Nlog2N ),故在处理大点数运算时能获得大幅改善,该算法现在又称为radix-2算法。
FFT实际上就是将一个序列分解成两个或更多的较短序列,计算一个序列的运算次数是直接DFT的运算次数的一半,来达到傅里叶变换的快速运算,而分解的序列是完整的原序列。由此将对时间序列,和对傅立叶变换序列进行处理可以将FFT细分成两种算法:按时间抽取算法(DIT)、按频率抽取算法(DIF).
radix-2算法除了在运算复杂度方面获得大幅改善外,算法本身还具有运算规律性的优点,因此非常适合用 FPGA实现,为了能在实现上减少硬件面积及消耗功率,许多以硬件实现为优先考量的 FFT 算法相继被提出如He-Torkelson 算法。
2.1.1 radix-2FFT算法简介
长度为N的有限长序列x(n)的DFT的表达式为
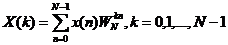 (2-1)
(2-1)
X(N)通常是一个复杂的序列。如果X(k)的值根据公式(2-1)直接计算,对于一定的k值,计算时复数乘法加N次同时复数加法也加(N-1)次。然后对于N 个k值,计算时复数乘法加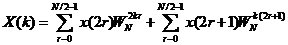 次以及复数加法加N(N-1)次。当Ngt;gt;1时,N(N-1)≈
次以及复数加法加N(N-1)次。当Ngt;gt;1时,N(N-1)≈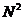 。上面的说明中可以看出,N点DFT的乘法和加法运算次数均与
。上面的说明中可以看出,N点DFT的乘法和加法运算次数均与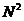 成正比[[7]]。对N取大值来说,计算量是十分庞大的。假设N取32,将达到1024这样一个计算的巨大量,很难实现用于实时信号处理。因此,为了能高速有效地计算出DFT的结果,就必须想办法缩小计算次数。
成正比[[7]]。对N取大值来说,计算量是十分庞大的。假设N取32,将达到1024这样一个计算的巨大量,很难实现用于实时信号处理。因此,为了能高速有效地计算出DFT的结果,就必须想办法缩小计算次数。
如上所述,N点DFT的复数乘法数目等于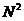 。N点DFT可以看作是被分解的几个较短的DFT。基于这种想法,N点DFT可以被分解成几个较短的DFT,使得乘法的数量将大大减少,显著减少DFT计算量。此外,对旋转因子
。N点DFT可以看作是被分解的几个较短的DFT。基于这种想法,N点DFT可以被分解成几个较短的DFT,使得乘法的数量将大大减少,显著减少DFT计算量。此外,对旋转因子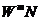 来说,其周期性表现为:
来说,其周期性表现为:
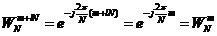 (2-2)
(2-2)
其对称性表现为
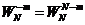
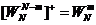 (2-3)
(2-3)
所以FFT算法的一般思路就是将初始待处理DFT分解成几个短序列的DFT,再把得到的DFT继续转换,并且由于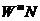 具有周期性和对称性,可以将DFT的运算次数再减半。FFT算法一般使用的有radix-2、radix-4和radix-8FFT几种。radix-2中的N=
具有周期性和对称性,可以将DFT的运算次数再减半。FFT算法一般使用的有radix-2、radix-4和radix-8FFT几种。radix-2中的N=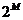 ,即一定长度的N值肯定会和2的整数次幂吻合。用8点的FFT做代表,说明radix-2FFT算法。
,即一定长度的N值肯定会和2的整数次幂吻合。用8点的FFT做代表,说明radix-2FFT算法。
2.1.2 radix-2FFT算法基本原理
radix-2FFT算法例如上文提到的时域抽取法FFT(DIT-FFT),一般讨论两种算法,而原理大致是一致的:另一种是频域抽取法FFT(DIF-FFT)。所以这两种算法中下面主要介绍DIT-FFT算法。本论文采用的就是DIT-FFT算法。
设序列x(n)的长度为N,并且有以下的条件成立
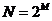 ,M为自然数 (2-4)
,M为自然数 (2-4)
按n的奇偶性对其转换,得到x(n)的两个子序列x1(r)和x2(r),它们的值为N/2,如(2-5)(2-6)式
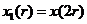 ,
,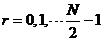 (2-5)
(2-5)
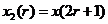 ,
,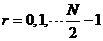 (2-6)
(2-6)
那么x(n)的DFT为
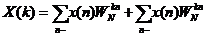
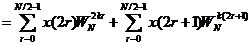
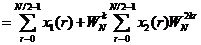 (2-7)
(2-7)
由于
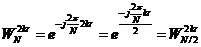 (2-8)
(2-8)
所以
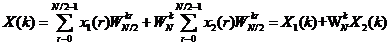 (2-9)
(2-9)
其中k=0,1,…,N-1。x1(r)和x2(r)进行分解,得到了X1(k)和X2(k),即
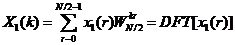 (2-10)
(2-10)
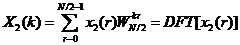 (2-11)
(2-11)
又由于X1(k)和X2(k)都是以N/2为周期,且
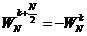 (2-12)
(2-12)
所以X(k)又可以表示为如下所示的表达式
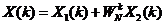
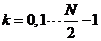 (2-13)
(2-13)
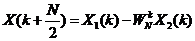
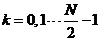 (2-14)
(2-14)
这样的N点DFT被分成的DFT的两个长度为N / 2的点。方程(2-7)和(2-8)示出了一开始的N点的DFT和两个N / 2点的DFT之间的关系。通常,用于随后的说明的方便,可以同许多其他文章中,式(2-13)和(2-14)的操作也由图2.1中所示的流程图符号表示。由于这种流图符号看起来像一只蝴蝶,它被称为蝶形运算符号[[8]]。
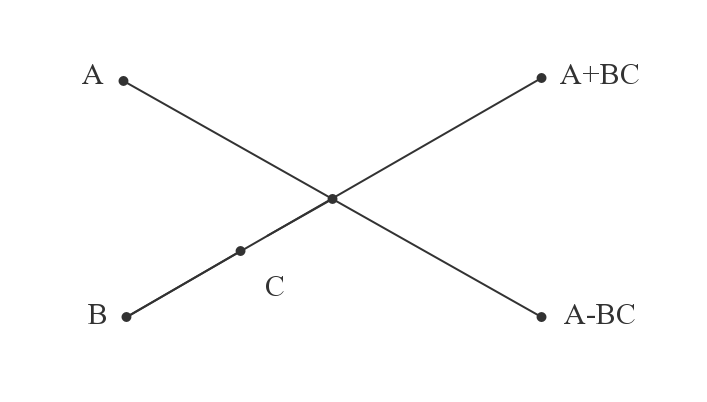
图2.1蝶形运算符号
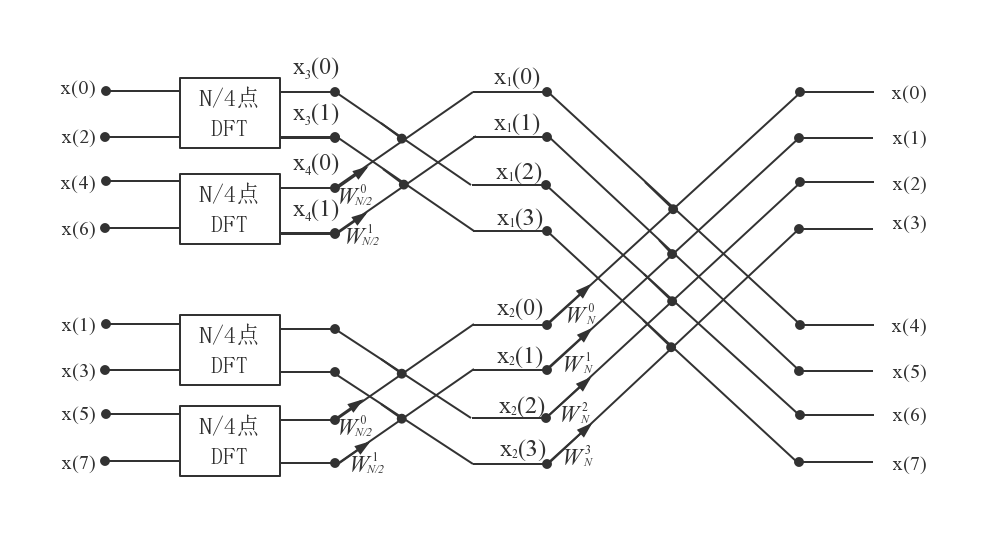
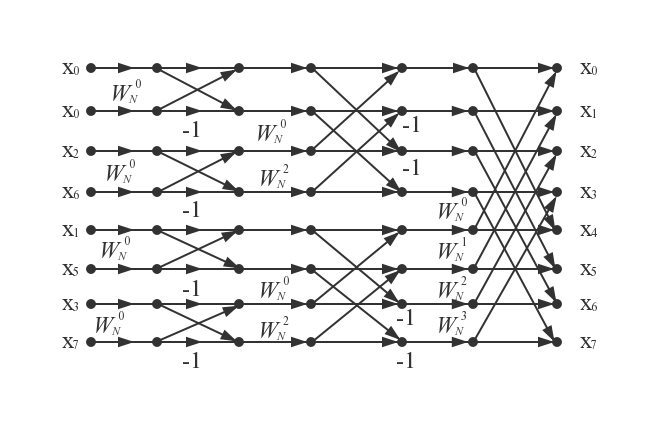
使用蝶形运算符的这种方法,图2.2可以用于表示上文描述的变换操作。在图2.2中,N=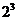 =8,式(2-13)给出了计算X(0)~X(3)的方法,和式(2-14)给出了计算X(4)~X(7)的方法。
=8,式(2-13)给出了计算X(0)~X(3)的方法,和式(2-14)给出了计算X(4)~X(7)的方法。
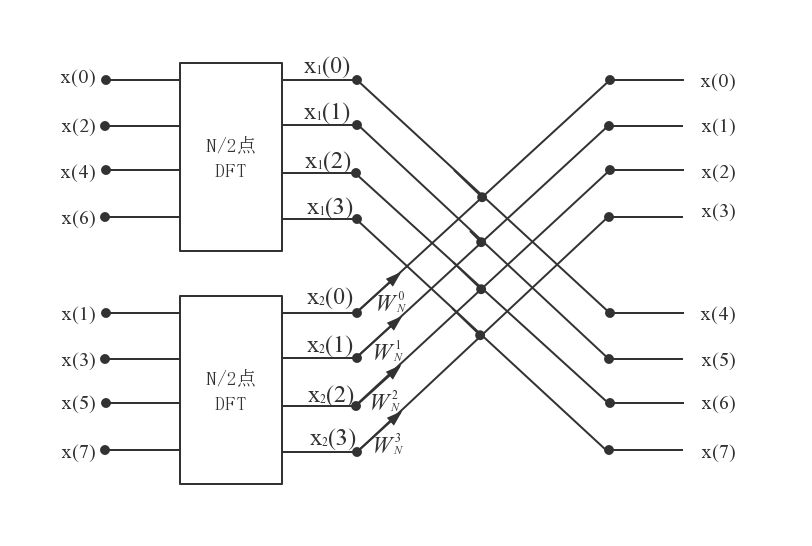
图2.2 N点DFT的一次时域抽取分解图(N=8)
从图2.1中可以看出,复数乘法加一次、复数加法加两次构成一次蝶形运算。从图2.2可以看出,在分解之后,经过计算两个N / 2点DFT和N / 2次蝶形运算得出N点DFT。从前面的描述可以看出,计算一个N/2点DFT需要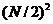 次复数乘法、N/2(N/2-1)次复数加法。所以,根据图2.2,计算N点DFT共需要
次复数乘法、N/2(N/2-1)次复数加法。所以,根据图2.2,计算N点DFT共需要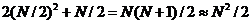 (Ngt;gt;1)次复数乘法和
(Ngt;gt;1)次复数乘法和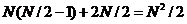 次复数加法运算。从比较中可以得到,只进行这样的单次分解就减少近一半的计算量,这充分证明了这种分解在减少DFT的计算量方面非常有效。由于此处N=
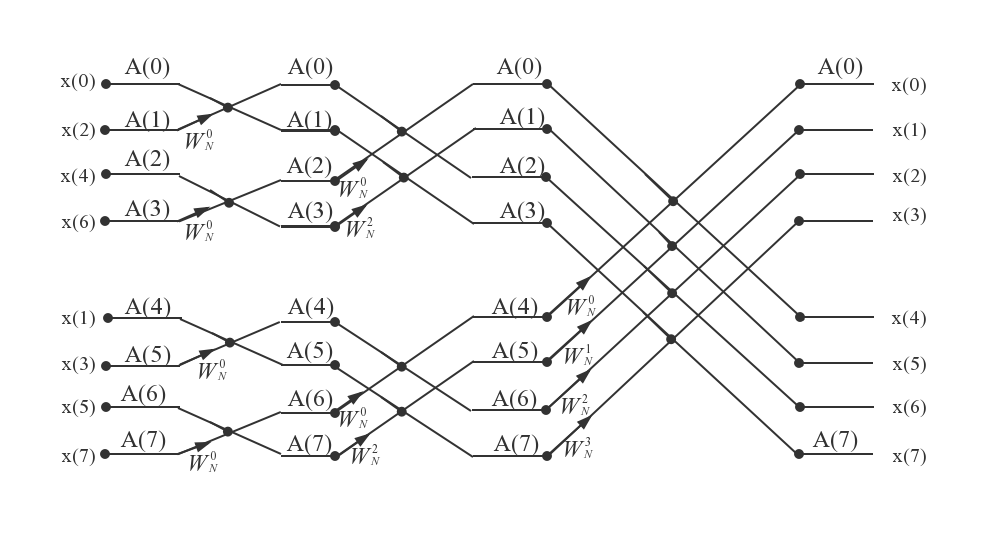
次复数加法运算。从比较中可以得到,只进行这样的单次分解就减少近一半的计算量,这充分证明了这种分解在减少DFT的计算量方面非常有效。由于此处N=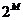 ,N/2仍为偶数,为了使计算量进一步减小,可以通过遵循先前方法进一步分解N/2点DFT。
,N/2仍为偶数,为了使计算量进一步减小,可以通过遵循先前方法进一步分解N/2点DFT。
与第一次分解一样,x3(l)和x4(l)是由原先X1(k)和X2(k)得到的,是x1(r)按奇偶分解处理的,即
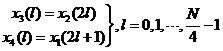 (2-15)
(2-15)
那么,X1(k)又可表示为
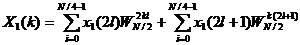
=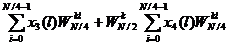
=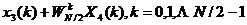 (2-16)
(2-16)
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: