NSGA-II算法在能量约束单拆卸线平衡问题中的应用研究开题报告
2020-04-02 11:22:59
1. 研究目的与意义(文献综述)
1.1 研究目的及意义
进入 21 世纪,为了应对资源紧缺和环境污染问题,各国政府相继建立法律法规,要求生产者对寿命终结(end of life,eol)的产品进行回收、拆卸、再利用,从而实现资源的循环利用和保护环境的目的,同时围绕eol产品的拆卸与回收是再制造中的重要一环。制造企业对废旧产品进行回收再利用,既顺应法律法规的要求,同时又可以降低生产成本,增加企业的经济效益。因此,越来越多的制造企业参与到废旧产品回收再利用的实践中[1]。
拆卸线平衡(dlb)问题是将一组分解任务分配到一个有序的工作站序列的过程,以优化一些性能度量(例如,站点数量、危险组件数量、周期时间和工作负载)。产品拆卸操作是一种系统的方法,它从产品中移除一部分或一组零件或部件,或将产品分解为一个给定的目标,指从产品中系统地分离零件、组件、部件或其他零件集合体的过程,产品只有经过拆卸才能实现材料的回收和可用零部件的再造[2]。拆卸作业的完成既可以在单个拆卸工作站或拆卸工作单元上进行,也可以在产品拆卸流水线上进行。
2. 研究的基本内容与方案
2.1研究内容
围绕EOL产品的拆卸与回收是再制造中的重要一环,当前工业机器人已广泛应用于EOL产品拆卸线。本课题重点研究考虑机器人能量约束的单拆卸线平衡问题,在对该问题进行理论建模和分析的基础上,基于NSGA-II算法,研究并提出解决该问题的多目标进化算法,最后通过仿真实验对所提算法的性能进行分析。
具体研究内容包括:
(1)在传统约束集中引入机器人能量约束,并考虑周期时间确定情况下的工作站数量最小,总能量约束最小的多目标优化问题,研究并建立该问题的最优化数学模型;
(2)研究上述最优化模型在单目标情况下的最优化,选择工作站数量小这个优化目标,将上述模型转化为单目标最优化模型,并使用CPLEX优化软件对单目标最优化模型进行编码求解,获得最优解;
(3)针对上述最优化模型无法解决大规模数据集的问题,研究基于进化算法的元启发式算法的设计。选择一种进化算法(NSGA-II算法)作为基本的算法框架,研究并设计适合本课题所研究问题的编解码、初始化流程、交叉及变异算子,最终提出一种解决所研究问题的进化算法;
(4)对上述提出的进化算法进行编码实现,并通过与其他进化算法的仿真分析,分析比较所提算法的性能。
2.2研究目标
本研究中,基于第二代非支配排序进化算法(NSGA-II算法),利用其降低了非劣排序遗传算法的复杂性、运行速度快和解集的收敛性好的优点[24],考虑机器人在拆卸线上的能量约束,研究解决机器人能量约束的单拆卸线平衡问题的多目标进化算法。
具体阶段目标如下:
(1) (1)研究并建立一种针对能量约束单拆卸线平衡问题的多目标最优化数学模型。
(2) (2)完成基于CPLEX最优化软件的单目标最优化问题的最优解求解。
(3) (3)研究并建立一种针对本课题所研究问题的多目标进化算法(NSAG-II算法),并完成该算法的性能分析工作。
2.3研究拟采用的技术方案
该项研究的核心技术是NSGA-II算法的应用,并解决机器人能量约束单拆卸线平衡问题, 目标是在确定的周期内尽量减少资源和工作站的数量。
具体需要采取的技术方案及措施如下:
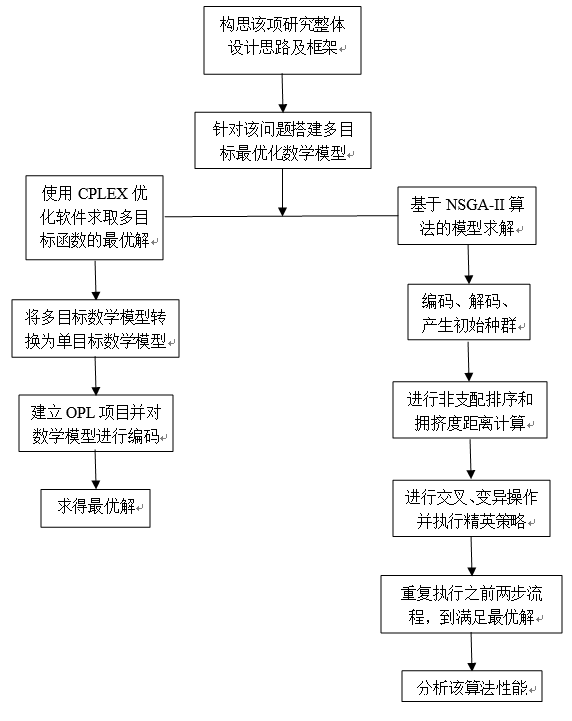
(1) (1)针对能量约束的单拆卸线平衡问题,搭建由目标函数、约束条件、决策变量等组成的数学模型。在该数学模型中,最小化工作站数量作为目标函数,将周期时间、任务数等作为约束条件,相应地设置决策变量。
(2) (2) 针对数学模型求取最优解,使用CPLEX最优化软件建立OPL项目,将之前最优化数学模型中的目标函数、约束条件及决策变量等使用OPL语言表示出,同时完成对数学模型的编码求取最优解。
(3) (3)基于进化算法的设计,采用NSGA-II算法作为基本的算法框架。首先,针对该项研究中的问题初始化种群产生一定数量的个体,将种群中的个体按照非支配排序,通过选择、交叉、变异算子得到子代。其次,从第二代开始,将父代种群与子代种群合并,进行非支配排序,同时对每个非支配层的个体进行拥挤度计算,从而选取合适的个体组成新的父代。最后,由此反复产生新的子代种群,直到满足多目标最优解结束。
 |
3. 研究计划与安排
(1)第1-3周:查阅相关文献资料,明确研究内容,学习毕业设计研究内容所需理论的基础。确定毕业设计方案,完成开题报告;
(2)第4-5周:熟悉掌握基本理论,完成英文资料的翻译;
(3)第6-9周:熟悉最优化建模方法和最优化软件的使用,完成数学建模和编码实现;
4. 参考文献(12篇以上)
[1] 赵忠,谢家平,任 毅.废旧产品回收再制造计划模式研究述评[j].管理学报,2008,5(2):305-311.
[2] 赵忠,刘贵华.基于遗传算法的产品拆卸线平衡问题研究[j].河南科学,2011,29(6):746-749.
[3] a roshani, d giglio. simulatedannealing algorithms for the multimanned assembly line balancing problem:minimising cycle time[j]. international journal of production research,2016,55(10): 2731-2751.




