摘 要

运动恢复结构（SfM）是利用一系列二维图像来重建场景或对象的三维结构的技术。图像实际上就是三维场景到二维平面的一个投影，只不过中间发生了一个维度的损失，因此我们没有办法从单个图像中确定投影线上的哪一个点可以与原图像点相对应。但是我们可以通过两个图像来找到两个相匹配的二维图像点所对应的原三维场景点。

本文主要研究了三维重建的主流方法增量式重建和全局式重建的具体算法实现，并且基于开源软件实现增量式重建和全局式重建的完整流程，以斯考克斯城堡作为重建对象，采用尺度不变特征变换（SIFT）的方式进行特征计算，使用ANNL2算法进行匹配计算，然后分别采用增量式重建和全局式重建方法完成三维重建，最后输出到多视图立体视觉显示接口（MVS）中显示三维模型，并对重建结果进行比较，最终发现两种方法优缺互补。

关键词：运动恢复结构；全局式重建；增量式重建；

Abstract

Stucture from Motion (SfM) is a technique that uses a series of two-dimensional images to reconstruct the three-dimensional structure of a scene or object. In fact, an image is a projection from a three-dimensional scene to a two-dimensional plane, but there is a dimension loss in the process, so we can not determine which point on the projection line can correspond to the original image point from a single image. But we can find the original three-dimensional scene points corresponding to two matching two-dimensional image points by two images.

This report mainly studies the implementation of incremental and global reconstruction algorithms, which are the mainstream methods of three-dimensional reconstruction. Based on the open source software, the whole process of incremental and global reconstruction is realized. With Sceaux Castle as the object of reconstruction, feature calculation is carried out by using scale invariant feature transform (SIFT), matching calculation is carried out by using ANNL2 algorithm. The incremental and global reconstruction methods are used to complete the three-dimensional reconstruction. Finally, the three-dimensional model is displayed in the multi-view stereo visual display interface (MVS). The results of the reconstruction are compared and the complementary advantages and disadvantages of the two methods are found.

Key Words:SfM;incremental reconstruction;global reconstruction;

目 录

摘 要 I

Abstract II

第1章 绪论 1

1.1 研究背景及意义 1

1.2 国内外研究现状 1

1.3 本文主要研究内容和结构 2

第2章 设计原理 3

2.1 针孔相机模型 3

2.2 内参矩阵和外参矩阵 5

2.2.1 定义 5

2.2.2 外参矩阵 6

2.2.3 内参矩阵和归一化相机 7

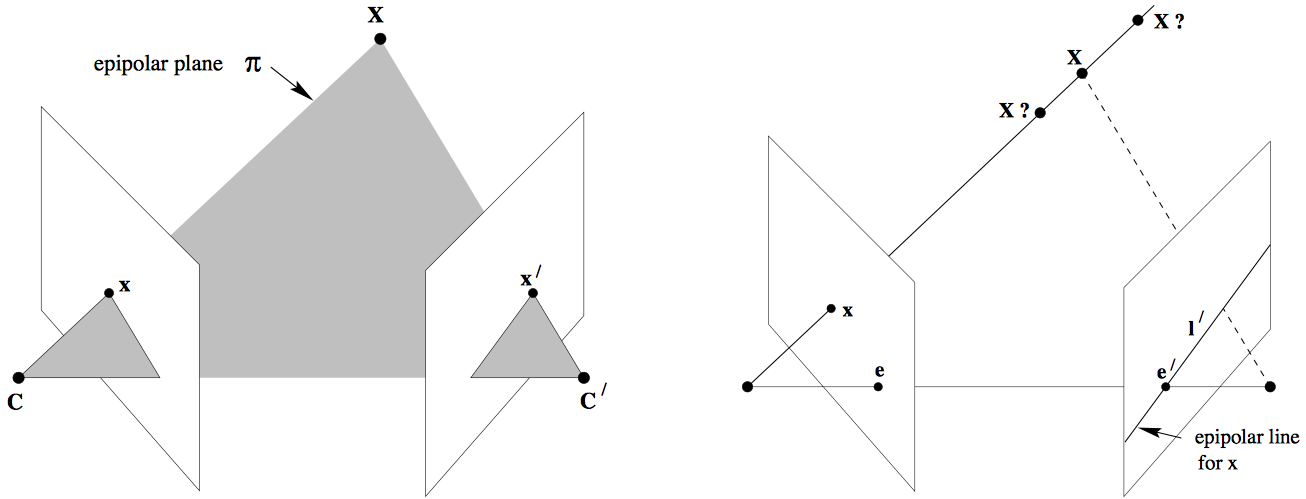
2.3 对极约束和基本矩阵 9

2.3.1 极线几何 9

2.3.2 基本矩阵 10

2.4 图像特征提取 10

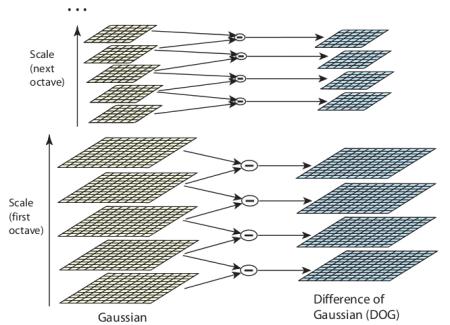
2.4.1 构建尺度空间 11

2.4.2 LoG近似 12

2.4.3 寻找关键点 13

2.4.4 消除不好的关键点 14

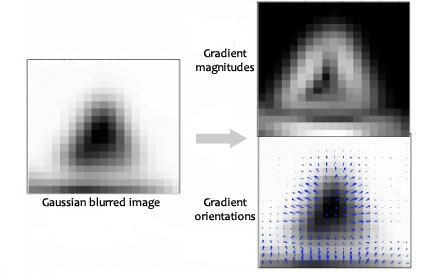
2.4.5 为关键点指定方向 15

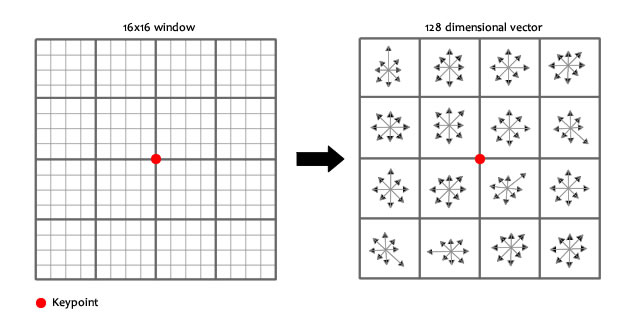
2.4.6 生成SIFT特征 16

2.5 图像特征匹配 17

2.5.1 最近邻匹配 17

2.5.2 基于k-d树的最近邻算法 18

第3章 系统实现 20

3.1 增量式重建概述及算法实现 20

3.2 基于开源软件的增量式重建实现 23

3.2.1 安装OpenMVG 23

3.2.2 安装OpenMVS 23

3.2.3 三维重建实现 24

3.3 全局式重建概述及算法实现 27

3.4 基于开源软件的全局式重建实现 28

第4章 结论与展望 30

参考文献 31

致 谢 33

绪论

研究背景及意义

这些年来我们一直对计算机图像通信、虚拟现实以及三维模型的内容通信存在着很大的需求，但是苦于构建三维模型所使用的嵌入式系统都采用了专用的硬件来完成，这不仅导致了很高的生产成本，还严重影响了新需求的产生和新技术的发展。但是摩尔定律告诉我们，我们其实可以在软件方面做更多的工作。Tomasi和Kanade提出了一种早期的方法。他们使用仿射分解方法从图像序列中提取3D^[1]。然而，正投影的假设是该系统的重要限制。

要创建三维重建，只需要从不同角度拍摄一个区域或一个高度重叠的物体的许多图像。相机不需要专门化，标准消费级相机很好地适用于SfM方法。这些图像通常是从一个移动传感器（例如无人机）上拍摄的，但也可以由一个人或多个人在不同的位置和角度拍摄。

专业软件包能够自动识别多个图像中的匹配特征。这些独特的特征通常是角落或线段。这些特征从图像到图像被跟踪，并用于产生相机位置和方向的估计以及特征的坐标。这会产生特征的x、y、z坐标点云。

虽然最低要求是在至少三个图像中可见特征，但建议尽可能多地获得SfM输入的图像（在合理范围内和可行性范围内）。为了获得最快的处理和模型质量，所有图像应该使用相同的相机同时拍摄，但这不是必需的。已经采用SfM方法使用众包图像来创建历史建筑和其他纪念碑的3D模型。三维点云通常在相对“图像空间”坐标系中生成，但可以使用地面控制点（GCP）和地理参考图像与真实世界坐标系统对齐。

SfM方法有许多应用。SfM可用于创建正射照片马赛克，三维点云和数字高程模型。正射影像马赛克在绘图和摄影测量中有很多应用。3D点云已被用于确定树木生物量，分析地质。从SfM处理创建的数字高程模型通常具有高分辨率，可用于检测地形变化以监测冰川、河流、沿海、坡地环境。除了自然资源和地理空间应用，SfM还广泛用于机器人和自动驾驶车辆。

国内外研究现状

运动恢复结构（SfM）的问题最早于1978年由麻省理工学院人工智能实验室在论文《The interpretation of structure from motion》中提出，之后1999年9月David G.Lowe在论文《Object Recognition from Local Scale-Invariant Features》中提出了尺度不变特征变换（SIFT）并于2004年再一次完善，尺度不变特征变换（SIFT）允许相应的特征匹配，即使在尺度和视角的大变化以及部分遮挡和变化照明的条件下。而后2006年Snavely等人在项目《Photo Tourism：探索3D中的照片集》中首次使用SIFT算法生成大型点云，并于2007年在国际计算机视觉杂志中刊登文章《从互联网照片集中模拟世界》。2012年Westoby等人发明了一种低成本、有效地利用SfM进行摄影测量的地球科学应用工具，同年James和Robson发明了一种使用相机直接准确重建3D表面和地形地地球科学应用并发表于地球物理学报。而三维重建在国内发展较晚，一直处于追赶的状态，与国外丰硕的研究成果相比还有一定差距^[2]。

本文主要研究内容和结构

本文主要研究室三维重建的两种主流方法：增量式重建和全局式重建，从几何以及算法的角度给出了两种方法的具体实现思路，并使用开源软件和公开数据集完成了增量式重建和全局式重建的实现。

第一章主要介绍了运动恢复结构这个研究课题的研究背景和意义、国内外的研究现状等等，基本上没有太多可讲的。

第二章主要介绍了三维重建的几何基础知识和图像特征提取和匹配的算法，从最简单的针孔模型开始，也是科学研究中消除轻量影响因素构建理想模型以简化问题研究成本的具体体现，然后通过线性代数中的矩阵建立起了三维场景实物与摄影成像之间的联系，最后通过三角测量来完成三维重建的关键步骤：生成三维点云。图像特征提取方面主要介绍了尺度不变特征变换（SIFT）算法，图像特征匹配方面主要介绍了k-d tree算法，这一部分是第二章进行三角测量的前提，只有完成了图像特征的提取和匹配后才能在几何上完成三角测量。

第三章分别利用开源软件和公开数据集完成了增量式重建和全局式重建，首先介绍了开源软件的安装与配置，然后利用开源软件所提供的运行库来编写python代码，最后完成全部的重建过程并生成了三维模型视图。

第四章主要介绍了课题研究中遇到的问题以及两种重建方法的优缺对比，然后本论文告一段落。

设计原理

针孔相机模型

我们将从一个非常简单的针孔像机模型开始介绍，其投影中心位于欧几里德坐标系的原点。设X3=f是投影平面，更简单地说是投影三维场景空间中的点的平面。它也被称为图像平面或焦平面。与针孔相机的映射相关的几何形状在图2.1中示出。该图包含以下基本对象：

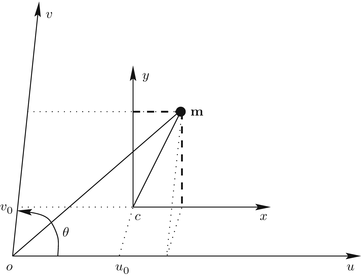
1. 三维正交坐标系，相机光圈刚好处在其原点的位置，命名为O点。然后X1轴、X2轴、X3轴分别是三维正交坐标系的三维主轴。其中X3轴平行于针孔相机的拍摄方向，所以被命名为光轴。然后X1轴和X2轴所形成的平面就是与针孔相机的成像平面平行的一个平面。
2. 成像平面，三维场景通过针孔相机投影所产生的平面。成像平面位于距X3轴负方向的原点O的距离f处，其中f是针孔摄像机的焦距。针孔像机的实际实现意味着成像平面被定位成使得它在坐标-f（当f gt; 0时）处与X3轴相交。
3. 在光轴和像平面的交叉点处的点R，该点被称为主点或图像中心。
4. 某处的点P在坐标（x₁，x₂，x₃）处相对于轴X1，X2，X3。
5. 点P进入相机的点线。也就是通过点P和点O的绿线。
6. 点P投影到图像平面上，表示为Q。该点由投影线（绿色）和图像平面的交点给出。在任何实际情况中，我们可以假设x₃gt;0，这意味着交叉点被很好地定义。
7. 在图像平面中还存在2D坐标系，其原点在R处，并且轴Y1和Y2分别与X1和X2平行。点Q相对于该坐标系的坐标是（y₁，y₂）。

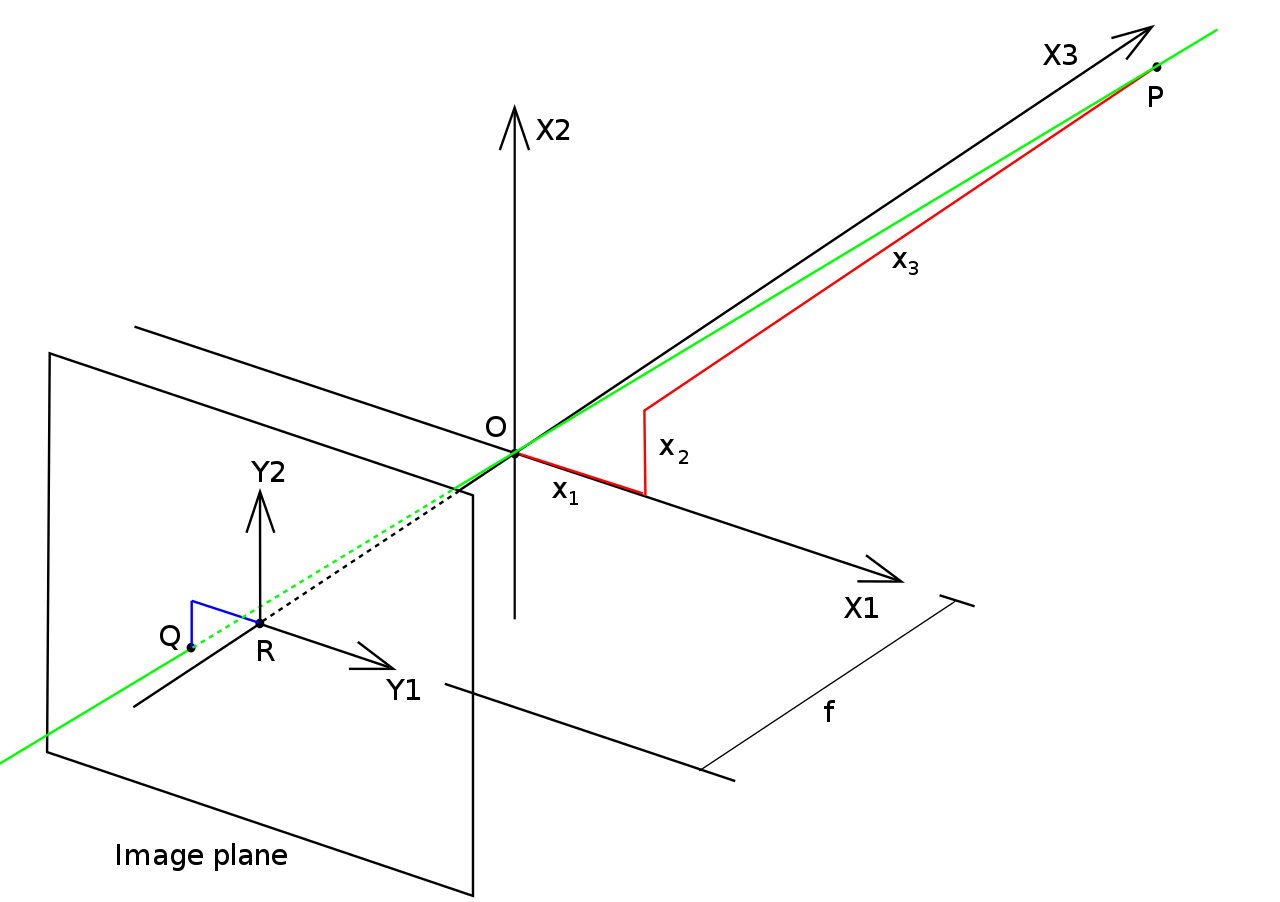
图 2.1 针孔相机模型

所有投影线必须通过的摄像机的针孔孔径被认为是无限小的点。在文献中，3D空间中的这一点被称为光学（或镜头或相机）中心^[3]。

接下来我们想要了解点Q的坐标（y₁，y₂）如何取决于点P的坐标（x₁，x₂，x₃）。这可以通过下图2.2显示与前一个相同的场景来完成。但现在从上面看，向下看X2轴的负方向。

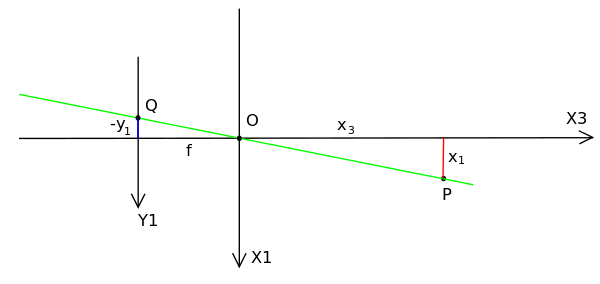
图 2.2 小孔成像模型

在这个图中，我们看到两个相似的三角形，两个都有投影线的部分（绿色）作为它们的斜边。左三角形的直角边是-y₁和f，右三角形的直角边是x₁和x₃。由于两个三角形相似，因此遵循以下这一点：

（2.1）

同理可得，从X1轴的负方向看有

（2.2）

以上可以概括为：

（2.3）

这是描述点P的3D坐标（x₁，x₂，x₃）与图像平面中的点Q给出的图像坐标（y₁，y₂）之间的关系的表达式。

由于实际摄影所得的照片和三维场景的方向是一致的，而我们现在所讨论的针孔相机模型成像的方向是实物通过旋转180度所得的，而成像尺寸则取决于成像平面到焦点的距离，所以为了方便研究我们通过以下办法来生成没有经过旋转的图像：放置图像平面，使其在f处而不是在-f处与X3轴相交，并重新执行先前的计算。这将产生在实践中不能实现的虚拟（或前）图像平面，但是提供了理论相机，其可以比真实相机更简单地分析。

在这两种情况下，从3D坐标到2D图像坐标的结果映射由上面的表达式给出，但是没有负号：

（2.4）

内参矩阵和外参矩阵

定义

相机参数是相机模型中用于描述场景中光线来源点的三维坐标与其投影到图像平面上的二维坐标之间的数学关系的参数。固有参数，也称为内部参数，是相机本身固有的参数，例如焦距和镜头畸变。外部参数，也称为外部参数或相机姿态，是用来描述相机与其外部世界之间转换的参数。在计算机视觉中，为了了解相机周围的环境，我们首先要知道相机的参数。根据我们需要达到的精度和相机的质量，一些参数可以忽略。例如，对于高质量的相机，在大多数应用中镜头畸变通常可以忽略^[4]。

在入口透视相机中，我们仅用一个参数（焦距f）来描述透视相机的数学模型。三维点与其图像投影之间的关系描述为：

（2.5）

其中s=S是任意非零标量，P是由下式给出的投影矩阵：

（2.6）

外参矩阵

在上面概括的条目透视摄像机中描述的投影投影矩阵中，我们假设3D点在摄像机坐标系中表示。实际上，它们可以在任何3D坐标系中表示，有时也称为世界坐标系。

如图2.3所示，我们从以光学中心C（摄像机坐标系）为中心的旧坐标系到以点O（世界坐标系）为中心的新坐标系，通过平移t=CO进行旋转。然后，对于单个点，其在摄像机坐标系M_c中表示的坐标和在世界坐标系M_w中表示的坐标通过以下方式相关联：

（2.7）

或者表示的更简单：

（2.8）

其中D是三维空间的欧几里德变换：

（2.9）

矩阵R和矢量t描述了针孔像机相对于世界坐标系的方向和位置，因此它们被称为像机的外部参数^[5]。

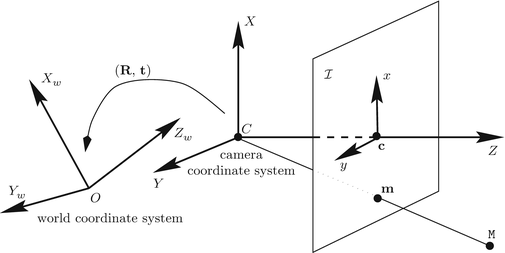
图 2.3 世界坐标系和摄像机外部参数

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：