复杂场景中多椭圆目标的检测及实现毕业论文
2020-04-12 14:22:35
摘 要
椭圆检测是图像处理的一个热点问题,由于椭圆目标广泛存在于社会、经济、军事等各个领域,且人们出于各种需求对它进行提取,因此如何高效、准确的检测出这些椭圆形物体,具有重要的应用及学术研究价值。
本文基于主元素法,对前景提取后的样本区域进行多椭圆拟合。首先,在样本提取阶段,采用阈值法从场景中提取出二值前景目标;其后,采用一个椭圆来拟合场景中的目标区域,通过设计的拟合评价指标来判断拟合的误差,如果误差小于预定阈值,则结束运行;如果误差大于阈值,则根据拟合误差新添一个椭圆,并基于EM算法,优化各个椭圆的参数,包含椭圆中心,长轴、短轴、及长轴方向;再次进行拟合误差计算,并重复上面各步骤,直至拟合误差达到要求。
采用本文设计的方法,对各种复杂的前景目标进行椭圆分析,可以较好地从中检测、分割出各种类椭圆目标。其肉眼精度及量化误差都符合实际应用的要求,相关实验验证了本文算法的有效性。
关键词:多椭圆检测 EM算法 主元素法
Abstract
Ellipse detection is a hot issue in image processing. Because elliptical targets are widely used in various fields, such as society, economy, military and other fields, people extract them out of various needs. Therefore, how to detect these elliptical objects efficiently and accurately has important and academic research value.
Based on the principal element method, multi ellipse fitting is applied to the sample area after foreground extraction. First, in the sample extraction stage, the two value target is extracted from the scene by the threshold method. Then, an ellipse is used to fit the target area in the scene, and the fitting error is judged by the designed fitting evaluation index. If the error is less than the predetermined threshold, the error is over. If the error is greater than the threshold, then the root is the root. According to the fitting error, a new ellipse is added, and the parameters of each ellipse are optimized based on the EM algorithm, including the ellipse center, long axis, short axis and long axis direction, and the fitting error is calculated again, and the above steps are repeated until the fitting error is reached.
The elliptical analysis of various complex foreground targets can be achieved by using the method designed in this paper. Its gross accuracy and quantization error meet the requirements of practical application. Relevant experiments verify the effectiveness of the algorithm.
Key words: multi-ellipse detection, EM algorithm, principal element method
摘要 III
第1章 绪论 1
1.1课题研究的背景及意义 1
1.2椭圆检测算法的研究现状 1
1.3算法内容及论文结构安排 2
第2章 椭圆拟合算法简介 4
2.1图像预处理 4
2.1.1灰度化图像 4
2.1.2二值图像 4
2.1.3边缘检测 5
2.2Hough变换方法 6
2.2.1Hough变换算法描述 6
2.2.2Hough变换算法存在的问题 8
2.3最小二乘法 8
2.3.1最小二乘法描述 8
2.3.2最小二乘法存在的问题 9
2.4本章小结 9
第3章 EM算法原理 10
3.1 EM算法的数学理解 10
3.1.1 最大后验概率 10
3.1.2 Jensen不等式 11
3.2 EM算法的思想及算法描述 12
第4章 基于EM算法及主元素法的椭圆拟合法 14
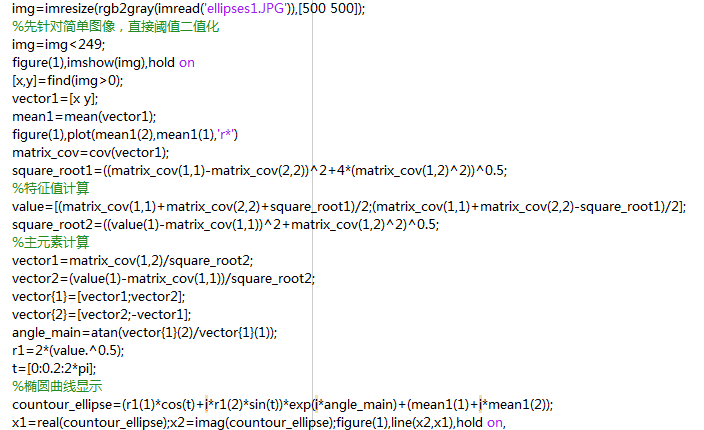
4.1主元素法拟合椭圆原理 14
4.2多椭圆目标检测的EM算法设计 16
第5章 本文算法的实际拟合结果与总结 18
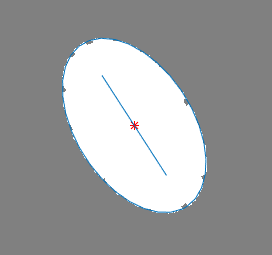
5.1 单椭圆目标拟合结果 18
5.2 多椭圆目标拟合结果 20
5.3 拟合结果结论 21
第6章 总结与展望 22
6.1全文总结 22
6.2不足与展望 22
参考文献 23
致谢 25
第1章 绪论
1.1课题研究的背景及意义
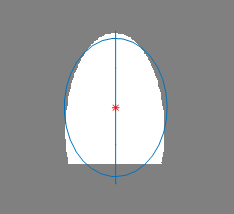
自二十世纪以来,图像识别随着计算机的不断进步而飞速发展。在图像识别的图形识别中,椭圆识别的发展尤为突出。虽然在日常中圆形较多,但由于拍摄角度问题及其他情况的影响下,大部分圆形物体的形状都会映射成椭圆形,所以多数情况下椭圆识别要比圆形识别具有更高的重要性。比如,在商业领域中的商标检测、机械制造领域的零部件识别、安保系统里的虹膜识别、军事领域中的目标跟踪系统等都用到了椭圆识别技术。伴随椭圆检测的飞速发展,如果能从图像中得到部分椭圆的参数信息,经过计算后甚至可以给三维建模的目标进行定位。
除上述实际用途之外,椭圆拟合技术在科研领域上也得到了非常广泛的应用。首先在医学方向上,椭圆检测技术可以被用于检查病人的脉管横切面或者类椭圆形的组织器官,比如心脏、血管、骨骼、瞳孔甚至细胞等,在外科中还可以用来检测固定骨头的骨钉的位置。在生物领域,椭圆检测可以用来检测微生物的形状和染色体上的细胞膜等。在模式识别方面,例如指纹的识别,通过记录椭圆特征值来记录人的指纹特征。在天文学上,我们可以利用椭圆拟合对天文图像检测外星火山口或者陨石坑......这些都需要利用到椭圆检测技术。
椭圆检测在图像处理中是一个重要的领域,随着技术不断的发展和成熟。人们发现很多物体都有椭圆形状,椭圆的图形在自然界各处都有体现。因此,如何能够高效并准确的检测出具有椭圆形状特性的物体,是椭圆检测的重要发展方向。
1.2椭圆检测算法的研究现状
近些年来,几何图形识别已经渗透在人们的日常生活中,其中椭圆检测的重要性愈加突出。最初,椭圆拟合是用来拟合圆锥曲线的,通常都是利用最小二乘法来拟合。该但是该方法不一定能保证拟合出的结果一定是椭圆曲线,有一定可能出现多条二次曲线。还有一种比较常用的椭圆检测算法随机Hough变换,对噪声点和孤立点都具有良好的鲁棒性,但是,Hough算法需要计算椭圆的5个参数,换句话说是要在五维空间内给样本点做投票,这样计算量会大大增加。虽然Hough变换可以进行降维操作,但该算法计算在时间与空间复杂度上的消耗仍然很大,实现起来有一定困难。最小平方中值法在用在椭圆检测上后,该方法确实能很好的解决最小二乘法在拟合椭圆时对噪声和孤立点的敏感性,但也存着在以下的缺点:最小平方中值法每次至少需要采五个样点来计算椭圆的参数,在运算过程中无法确定所需计算的次数,并且在样本选取的方式会对拟合出的椭圆有较大的影响。
20世纪以来,图像处理随着计算机的不断进化而逐渐走进学者们的世界。尤其是在1962年PaulHough提出Hough变换后,由于其能将图像信息转换到参数空间来计算,而且具有一些明显的优秀性质,引起了很多学者的注意力。近几十年来,国内外学者对Hough变换进行了广泛的扩展,在很多领域上都有很多有价值的成果。陈燕新等利用梯度信息提出了一种能够解决无效采样的随机Hough变换改进算法,但是没能解决Hough变换对噪声比较敏感的问题;韦宏强利用Hough对椭圆上的对偶点进行投票提取图像型心,从而优化Hough变换耗时长的缺点,但该算法无法对长轴短轴缺失的椭圆进行检测;为了解决长短轴缺失的情况,王春芳等所提出的将弧段在象限中体现,通过三个象限内的弧段来确定同一个椭圆的方法对重叠椭圆以及图片噪声都有效,但不适用于被遮挡大部分区域的椭圆目标;陆路提出基于椭圆对偶点性质的Hough变换拟合椭圆法,能够对前者的CMHT算法进行精确度改进,但是运算速度增加较多;李艳荻等提出的利用椭圆弦与切线间的特征性质来对随机Hough变换进行改进,在精确度和速度间找到了个较平衡的点;胡瑞欷等对于openCV中椭圆识别函数cvFitEllipse2()进行了优化处理,可以稳定的提取螺纹孔板上的椭圆孔洞,但该算法在优化过程中将圆心距离较近的椭圆只保留一个,这样处理对于重叠椭圆会造成部分无法识别的情况;吕洪赫等基于椭圆的对称性,对传统的最小二乘拟合法进行优化,但对于椭圆残缺度过高导致长轴缺失的情况,该算法将会退化到最小二乘法;薛程等对当前的大部分椭圆检测算法进行了一次总结与展望,并且认为Hough变换虽然有很多优势,但同时也存在了很多不可忽视的缺点例如耗时长,计算量大等缺点;韩建栋等采用了主元变换法进行多椭圆检测,但该算法无法对重叠椭圆进行处理。
1.3算法内容及论文结构安排
本文算法设计在matlab2015b环境下实现,通过调用matlab封装的库函数以及设计的功能函数,完成对算法功能的实现。算法流程图如图1.1所示。
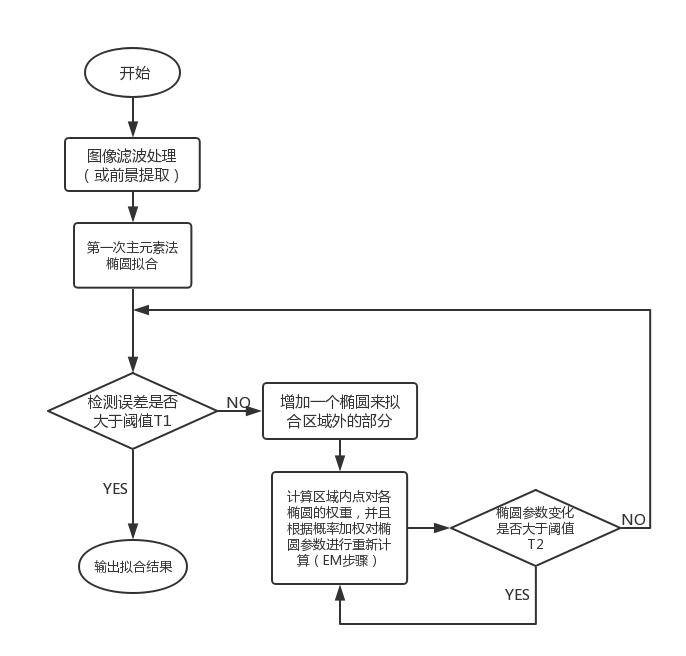
图1.1算法整体流程图
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: