英语原文共 20 页，剩余内容已隐藏，支付完成后下载完整资料

使用贝叶斯模式平均来校准预报集合

ADRIAN E. RAFTERY, TILMANN GNEITING, FADOUA BALABDAOUI, AND MICHAEL POLAKOWSKI

Department of Statistics, University of Washington, Seattle, Washington

摘要

用于概率天气预报的集合经常表现出离散误差的相关性，但他们往往是偏小离和的。本文提出了一种基于贝叶斯模式平均（BMA）的后处理集合的统计方法，它是组合不同来源的预报分布的标准方法。BMA预测概率密度函数（PDF）是集中于个体偏差校正预报PDF的加权平均，被该权重等于所述模型生成预测的后验概率和反映模型在训练期对预报技巧的相对贡献。

该BMA权重可以被用来评估集合成员的有用性，并且这可以被用来作为选择集合成员的基础;这在给出运行大集合的成本时是有用的。该BMA的PDF可以表示为任何所需大小的非加权集合，通过BMA预测分布的模拟。

该BMA预测方差可以被分解成两个分量，一个对应于预报之间的变率，第二个对应于预报内的变率。仅仅基于集合离散误差的预测PDF或间隔只包含第一部分但没有第二部分。因此，BMA提供集合趋势的理论解释，呈现出离散误差相关性，但仍然是偏小离和的。

该方法被用于华盛顿大学的第五代宾夕法尼亚州立大学-NCAR中尺度模式（MM5）集合西北太平洋2000年1-6月表面温度48小时预报。预测的PDF比原始集合 有更好的校准，并且BMA预测的90％BMA预测区间更加集中比那些样品气候产生的平均缩短66％。作为副产品，BMA产生一个确定的点的预报，并且它的均方根误差比具有比最好的集合成员的低7％，比集合平均值低8％。对于海平面气压的预测也得到了类似的结果。模拟实验表明，当优先的集合被校准时，BMA表现相当不错，甚至过度离散。

1.引言

做概率天气预报的占主导的方法一直是使用集合预报，就是模型在不同的初始条件或模式物理下多次运行。这是利斯（1974年）提出的，为实现由爱泼斯坦（1969）提出的总体框架的一种方式。基于全球模式的集合预报已发现在中尺度的概率预报中是有用的。(Toth and Kalnay 1993; Molteni et al. 1996; Houtekamer and Derome 1995; Hamill et al. 2000). 请键入文字或网站地址，或者上传文档。

取消

显示以下内容的翻译： Typically the ensemble mean outperforms all or most of the individual ensemble members, and in some studies a spread-error correlation has been observed, in which the spread in the ensemble forecasts is correlated with the magnitude of the forecast error.

仍然翻译： Typically the ensemble mean outperforms all or most of the individual ensemble members, and in some studies a spread-error correlation has been observed, in which the spread in the ensemble forecasts iscorrelated with the magnitude of the forecast error.

典型的集合平均优于个别集合成员的全部或大部分，并且在一些研究中离散误差的相关性已被观察到，其中在集合预报的离散与预测误差的量值相关。然而，通常的集合是偏小离和的并且因此没有校正。这两种离散误差的相关性和偏小离和的已在NCEP运行的全球集合(Toth et al. 2001; Eckel and Walters 1998),加拿大集合预报系统(Pellerin et al. 2003)，欧洲中期天气预报中心Buizza 1997; Buizza et al. 1999; Hersbach et al.2000; Scherrer et al. 2004)观测到。

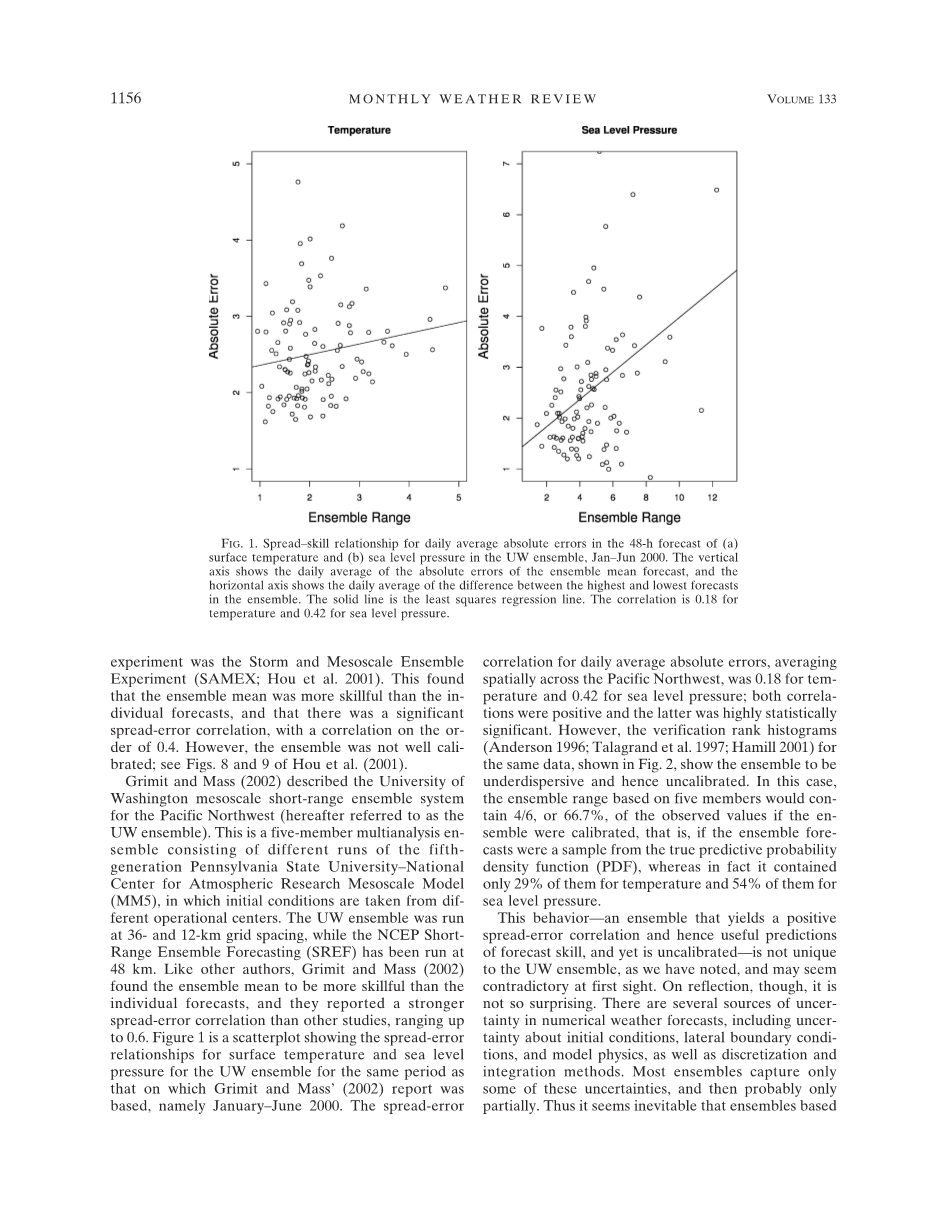
在这里，我们专注于短距离的中尺度预报。一些作者研究了利用天气集合，由15个NCEP RSM集合的成员,来进行短期预报(Hamill and Colucci 1997; Hamill and Colucci 1998; Stensrud et al. 1999). 由于这是中期预报的情况，集合平均对于短期预报来说，比单个集合成员更加有技巧，但离散误差技能的关系很微弱。第一个短期中尺度集合预报实验是风暴和中尺度集合实验(SAMEX; Hou et al. 2001). 这发现，集合平均比单独预测更有技巧性，并有显著的离散误相关性，相关性达到0.4。Grimit and Mass（2002）描述了为太平洋西北提出的华盛顿大学中尺度短期集合系统（以下简称为UW集合 ）。这是由第五代宾夕法尼亚州立大学，以及美国国家大气研究中心中尺度模式（MM5），其中初始条件是由不同业务中心采取的不同运行的五名成员组成的多分析集合。UW集合在36-和12公里的网格间距运行，而NCEP短期集合预报（SREF）是在48公里运行。像其他作者，Grimit和Mass（2002）发现的，集合平均比单独预报更加有技巧，而且他们报告了比其他研究更强的离散误差的相关性，范围可达0.6。图1是UW集合同期的表面温度和海平面气压的离散关系的散点图。对于日均绝对误差的离散误差的相关性，太平洋西北地区平均，分别为温度是0.18和海平面气压是0.42;两者的相关性是正的，并且后者统计上显著。

然而，对于相同数据的检验等级直方图(Anderson 1996; Talagrand et al. 1997; Hamill 2001) 展示在图2，展现集合是分散的，因此未校准。

在这种情况下，如果集合被校准，那么基于五个成员的集合范围将包含观测值的4/6或66.7％，也就是，如果集合预报是来自真实预报概率密度函数（PDF）的一个样本，那么实际上对于温度而言它只包含了其中的29％，对于海平面气压包含了其中的54％。集合产生了正的离散误差相关性并且产生了有用的预测技巧，但仍然是未校准的，UW集合并不是唯一的，正如我们已经指出，第一眼似乎是矛盾的。经过思考，虽然它不是那么奇怪。数值天气预报有几个不确定来源，包括关于初始条件，侧边界条件，以及模式物理过程的不确定性，以及离散和积分方法。大多数集合只能捕捉一些不确定，并且很可能只是部分。因此，集合单纯地依赖于扰动初始条件和侧边界条件，模式物理过程和积分方法将在一定程度上是偏小离和的似乎是不可避免的。因为他们捕获一些不确定性的重要来源，但是，即使在集合未经校准，得到了正的离散误差也是合理的。为了获得校准的预报PDF,因此，似乎需要进行某种形式的统计后处理，正如Hamill and Colucci (1997,1998)提出的。我们在这篇文章中的目的是提出一种方法从可能无法自行校准的集合的输出来获得未来的天气数量或事件的校准和尖锐的预报PDF。通过校准我们的意思是说，我们得到有概率P的间隔或事件，在从长远看，它们包含真值，或发生的时间比例P的平均水平。锐度是预测区间的宽度的函数。例如，在给定时间和空间检验90％预测区间被定义为一个下限和一个上限，使得在检验观测值位于两个边界之间的概率是被认为是90％。通过锐度，我们的意思是平均上预测区间上比气候所获得的窄。显然，越尖锐越好。我们采用的原则是，概率预报的目标是服从校准后锐度最大化(Gneiting et al. 2003)。

为了实现这一点，我们提出了一个统计方法来后处理集合预报，基于贝叶斯模式平均（BMA）。这是多存在竞争的统计模型，并在社会和健康科学被广泛应用到推理的标准方法;这里我们从动态模型扩展到预测。在BMA，整体预报PDF是根据每个单独的预测的预报PDF的加权平均;权重是估计后模式概率和反映训练期间模型的预报技巧，相对于其他模型。权重还可以用于选择集合成员：当它们小时就除去相应集合。这在给出运行集合的计算成本时是有用的。在BMA确定性预报仅仅是来自于集合的一个加权的线性函数平均值（可能的偏差校正）预测。该BMA的预报PDF可以写成解析表达式，并且它也可以表示为任何所需大小的均等加权集合，通过来自于预报PDF的可能观测值的模拟。在BMA预报的方差分解成两个部分，分别对应模型之间和内部模型的方差。集合离散仅捕获了第一个部分。该分解提供了在一些集合中所观察到的现象的理论解释和量化，其中一个正的离散误差相关与缺乏校准并存。在第2节我们描述BMA，展示BMA模式如何被估算，并给出BMA的例子。在第3节我们给出UW集合的BMA结果。在第4节，我们给一些模拟集合的结果，并在第5节我们讲几句结束语。我们的实验是与UW集合，也就是，一个中尺度，单模型，多分析集合系统，这样的思想也适用于其他情况，包括天气，扰动观测，奇异向量，多模式集合，具有小的变化，如下。

2.贝叶斯模式平均

a.基本思想

标准的统计分析，例如，回归分析，在一个假设的统计模式中典型地有条件地前进。通常，这种模式是从适合于数据的几种可能的竞争模式中选出来的，并且数据分析也不能确定它是最好的之一。其他可行的模式可以给出手头上科学问题的不同答案。这是得出结论时的不确定性来源，典型的做法就是，单一模式被认为是“最好的”，忽略了不确定性的根源，从而低估了不确定性。贝叶斯模式平均克服了这个问题，不是在一个单一的“最好”的模式，而是统计模型的整个集合。基于K个统计模式的训练数据预报变量y，整个概率法则告诉我们预报概率密度PDF，p(y)写作：,是单独基于模式的预报PDF，并且是模式的后验概率，并且反应了模式如何适应训练期数据的。后验模式概率相加等于1，就是它们可以被看做是权重。该BMA PDF是给每一个单独模型的条件PDF的后验模型概率加权平均值。BMA具有一系列的理论最优性能，并在多种模拟和实际数据的情况下具有出色的表现(Raftery and Zheng 2003)。现在，我们将BMA从统计模型扩展到动力模式。其基本思想是，对于任何给定预报集合有一个“最佳”的模式，或成员，但我们不知道它是什么，以及我们对最佳成员的不确定性是由BMA量化。再次，我们用y作被预报的量。每个确定性预报可以使用许多可能的偏差校正任何一种方法，得到的偏差校正的预报值。预报值与条件PDF相关，假定是集合的最佳预报。BMA预报模式是：，是后验概率，它们是非负的，并且相加等于1。对于气温、海平面气压等变量 条件PDF近似符合正态分布，其均值为原始回报结果的简单线性函数，标准差是sigma;，y丨~N（），其中为均值，sigma; 为标准差。 由此可知BMA为：E[y丨]=,也即BMA的确定性结果。

b.最大似然估计，EM算法，最小CRPS估计

若令是s.t分别表示空间与时间指标，表示第k个模式在空间s时间t的回报结果，则BMA的预报方差为V（y丨）=。BMA的预报方差包括两项，第一项是模式间的方差，第二项是模式内的方差。

BMA模型参数包括,,(k=1,2,hellip;,K)与sigma;，其中参数,(k=1,2,hellip;,K)，利用训练期的数据，采用线性回归来确定，而(k=1,2,hellip;,K) 与sigma;通过极大似然估计法来确定。假设预报误差在时间和空间上独立，则其对数似然函数为l()=.由于该对数似然函数不存在解析的极大值解，因而采用期望最大化算法（EM）求得数值解。文中引入一个非观测变量，当第k个模式是空间s时间t的最佳回报结果时，=1，否则=0。因而EM算法的迭代算法如下：

（1）初始化：令j=0，=1/K,=.

（2）计算初始对数似然函数

l()=.

(3)E步：令j=j 1,对所有的k,s,t计算

(4)M步：更新权重和方差

[,

更新似然函数l()。

（5）收敛性检查：如果l()- l()，停止迭代，否则回到第（2）步，继续迭代直到满足收敛，最终获得参数(k=1,2,hellip;,K) 与sigma;。

由于E步和M步迭代要保证收敛，在每一次的迭代中，对数似然函数是增大的，这意味着EM算法一般收敛到对数似然函数的局部最大值。因此，EM算法计算得到的解高度依赖于初值，且初值对收敛的影响很大。将训练期定义为一个滑动窗口，模型中的参数用每次滑动生成的新窗口计算得到。因而，训练期的长度对BMA模型参数的估计有影响，从而影响模式的回报结果。

c.BMA预报方差分解和离散误差相关性

BMA的预报方差为V（y丨）=。BMA的预报方差包括两项，第一项是模式间的方差，第二项是模式内的方差。

d.BMA的预报PDF

图3显示了BMA的预报的PDF。此PDF（示为图中的粗曲线）是五个标准PDF（组分是五细线）的加权和。分布是双峰的，反映了一个事实，有与彼

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[29652]，资料为PDF文档或Word文档，PDF文档可免费转换为Word