基于copula熵的流域站点相关性分析毕业论文
2020-02-28 23:23:20
摘 要
对于水文事件而言,研究流域站点间的相关性,对于流域站网的选址、优化以及合理开展水文资源的研究具有重要意义。针对现今水文站点间相关性研究方法的缺点与不足,本文提出了基于Copula熵计算流域站点间的互信息,通过构建站点日径流量数据的Copula函数,研究变量间的相关结构,计算出Copula熵,并采用蒙特卡洛发估计站点间的互信息,最后与由原始数据计算而来的相关系数作比较,分析Copula熵的可靠性。
以密苏里河流域奥萨格子流域中的五个站点信息为研究对象,实验结果表明,通过选择合适的Copula函数计算得到的互信息更能准确描述站点间的相关性;这五个站点间的互信息10组数据显示,奥萨格流域的这五个站点信息重叠的部分较多,信息的传递量较大,与相关系数比较,证实了Copula熵在水文事件相关性分析方面的可靠性。
关键词:Copula熵;互信息;水文事件;相关系数
Abstract
As for hydrological events, it is of great significance to study the correlation between river basin stations for the site selection, optimization and rational development of hydrological resources. For today's correlation research methods of hydrological site shortcomings and deficiencies, based on copulas connect entropy is proposed in this paper to calculate the mutual information between valley site, by building site daily runoff data of copulas connect function, research variables between the related structures, calculate the copulas connect entropy, and using monte carlo estimate the mutual information between sites, in the end the original data and calculation of the correlation coefficient for comparison, analysis of the reliability of copulas connect entropy.
River basin with the Missouri river valley osama grid of five site information as the research object, the experimental results show that by selecting suitable copulas connect function to calculate the mutual information more accurately describe the correlation between the site; The five sites 10 group, according to the mutual information between orszag river basin of the five overlap more site information, information transfer amount is larger, compared with the correlation coefficient, confirmed the copulas connect in hydrological event correlation analysis the reliability of entropy.
Key Words: Copula entropy; mutual information;hydrological events;correlation coefficient
目 录
第1章 绪论 1
1.1 研究目的及意义 1
1.2 国内外研究现状 1
1.2.1 水文相关性度量方法研究现状 1
1.2.2 Copula函数在水文分析计算中的应用 2
1.3 研究内容和技术路线 2
1.3.1 主要研究内容 2
1.3.2 技术路线图 3
第2章 Copula理论与互信息理论 5
2.1 Copula函数 5
2.1.1 Copula函数的基本性质 5
2.1.2 Sklar定理 5
2.2 Copula函数族 6
2.2.1 正态Copula函数 6
2.2.2 t-Copula函数 8
2.2.3 阿基米德Copula函数 10
2.3 基于Copula函数的相关性测度 16
2.4 Copula熵理论 17
2.4.1 Copula熵的定义 17
2.4.2 Copula熵的计算 17
2.5 互信息理论 17
第3章 基于Matlab的Copula函数的建立 18
3.1 实验对象及数据概况 18
3.1.1 实验对象概况 18
3.1.2 数据预处理 18
3.2 建立Copula函数 20
3.2.1 确定边缘分布函数 20
3.2.2 选取合适的Copula函数 21
3.2.3 参数估计 23
3.2.4 求得Copula函数 23
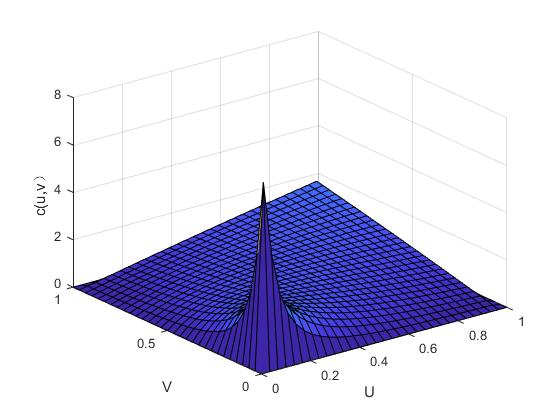
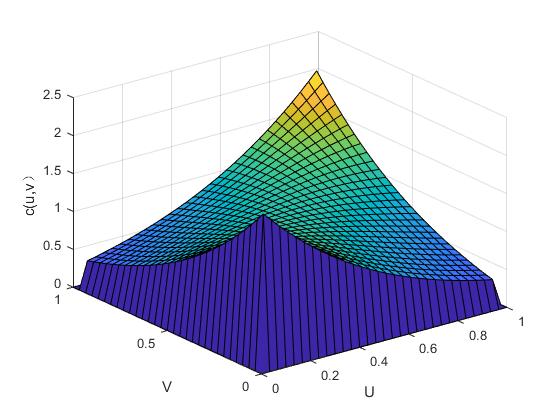
3.2.5 绘制Copula密度函数图 25
第4章 流域站点间互信息和相关系数的计算 27
4.1 基于Copula熵的流域站点间的互信息估计 27
4.2 基于SPSS的流域站点间的相关系数的计算 27
4.3 本章小结 27
第5章 总结与展望 29
参考文献 30
致 谢 32
- 绪论
- 研究目的及意义
水文事件的发生受到很多复杂的因素影响,它的发生会牵扯到频域、时域和时空域。而水文事件本身包含着多个方面的特征属性,这些属性之间一般具有相关性。[1]一般人们会通过研究流域站点空间布局间的信息相关性来评价和优化水文站网的空间布局,这也有助于展开水文水资源的研究和处理水文事件。目前,人们研究水文变量间的相关性分析方法一般采用Pearson线性相关方法。[2]但是这种方法首先要求随机变量必须服从多元正态分布,其次该方法只描述线性相关关系,并且不能够描述多元变量之间的相关性。但是在现实生活中,并不是全部的水文变量都是线性相关的。
近年来,人们开始把视线转移到Copula函数和信息论上,Copula函数可以刻画变量间的相关结构,来解决变量非线性、非正态的问题,信息论可以实现信息的数字化,两者的结合对于相关性问题的处理具有重要意义。在水文站网的优化和设计中,传统的站网设计方法有很大的局限性,它无法度量站点自身的信息量和站网间信息的传递量,如克里格法[3]和数理统计法[4]等。而互信息可以弥补这方面的不足,且互信息是一种非参数方法,对变量的函数形式没有任何限制。本文以密苏里河流域的五个站点为研究对象,采用Copula函数与信息论相结合的方法,即Copula熵,对密苏里河流域站点间的相关性进行分析,为站网的选址和优化提供依据。
- 国内外研究现状
- 水文相关性度量方法研究现状
- 国内外研究现状
水文事件中,度量变量间相关性的指标有很多,其中包括刻画全局相关性的相关系数、描述极值相关特征的尾部相关系数以及描述变量间信息传递量的互信息。
描述全局相关性的相关系数如Pearson相关系数、Spearson秩相关系数R以及Kendall秩相关系数,他们不能描述复杂变量的局部特征,只能刻画出全局关联程度。一般而言,描述的变量呈线性相关关系,R和均可描述变量间非线性相关关系。
尾部相关系数是重要相关性测度指标。它可用于度量极值理论,包括上尾部相关系数和下尾部相关系数。刘和昌等[5]以站点干旱历时与干旱烈度作为变量,利用SEC算法计算变量的经验尾部相关系数,以此来分析其尾部相关性问题,探究干旱频率问题;Poulin A等[6]通过对系族中七个Copula函数进行模拟,来比较其尾部依赖性。
互信息可以刻画变量之间的非线性关系,并且它度量的是变量间的信息传递量。若互信息越大,则变量间的相关性越强。赵铜铁钢等[7]利用互信息概念来判断神经网络径流预报模型中待选预报因子与预报变量间的相关关系; 龚伟等[8]利用互信息来分析水文变量高维非线性相关性以及度量水文模型的不确定性。
- Copula函数在水文分析计算中的应用
水文事件分析本身是一个集多特征变量于一身的复杂过程,且特征变量互相又有着复杂的相关性,因此找到一种方法来分析特征变量间的相关性至关重要,而多维联合分布能够有效地描述这些特征量,为解决多变量水文事件提供分析方法。近年来,Copula函数成为水文分析计算中的黑马,它能够灵活地刻画变量间的相关性结构,与其他函数不同的是,它所确定的联合分布函数是基于任意边缘分布,并且它可以有效地描述变量间的相关性。而Copula函数在多变量水文分析计算中的应用包括以下几个方面:
- 在洪水频率分析中的应用
Hou Y Y[9]等选择峰值、容积以及持续时间三个变量,并通过拟合的Copula函数估计三个变量的联合分布函数,有利于水工程方案的设计以及评估风险;Grimaldi S[10]等通过完整的分析洪水事件的三个主要特征变量,定义了三变量概率密度和累积分布函数,他们描述并模拟了这个函数的特性,以突出显示出与著名的对称阿基米德(Archimedean copulas)的不同之处。它们应用不对称分布来观测洪水数据,并比较用对称的copula和标准的Gumbel Logistic模型构建的分布结果;Favre等[11]分别采用P-Ⅲ型分布和Von Mises分布模拟年最大洪水量级和洪水发生时间的概率分布,并选用合适的Copula函数建立变量的联合分布,来分析两个变量的重现期。
- 在降雨频率分析中的应用
Bezak N等[12]利用三维Copula函数模拟峰值流量,水文体积和悬沙浓度数据的三变量频数分析;Vandenberghe S等[13]利用Copula函数构建多变量的无边缘分布函数,提供了详细的季节依赖性分析以及关于尾部依赖性的研究。
- 在干旱分析领域的应用
Shiau J T等[14]使用二维copula对联合干旱持续时间和严重程度分布进行建模,采用边缘推理函数法(IFM方法)构造copulas;肖名忠等[15]采用干旱历时、严重程度及最小流量表示水文干旱并利用三维Copula函数模拟了变量间的相关关系,为流域干旱分析提供了理论依据。
- 研究内容和技术路线
- 主要研究内容
- 研究内容和技术路线
如前文所述,目前Copula熵是很有前景的相关性分析方法,但对Copula熵方法的整体分析优势还未充分利用,对Copula熵方法的深入研究需引起更多关注。本文的主要任务是在Matlab平台中利用相关算法计算出某流域站点日径流量数据的Copula函数,结合信息论与Copula函数,估算出该流域站点的互信息,与Pearson及Kendall相关系数进行比较,判断Copula熵所计算出的互信息的可靠性。具体内容如下:
- 概述Copula函数理论、Copula函数族以及对应图像的分布特征;阐述信息论,并将Copula函数与信息论结合,估计变量间的相关性。
- 基于Matlab建立Copula函数,利用Matlab中所包含的Copula函数方法求取最优Copula函数。
- 使用蒙特卡罗法计算互信息,利用互信息与Copula熵的函数关系,提高互信息的估计精度。
- 由原始数据得到Spearson秩相关系数和Kendall秩相关系数,对比由Copula熵计算得到的站点间的互信息,分析Copula熵估算互信息的可靠性。
- 技术路线图
本文总体结构框架及技术路线图如下图1.1所示:
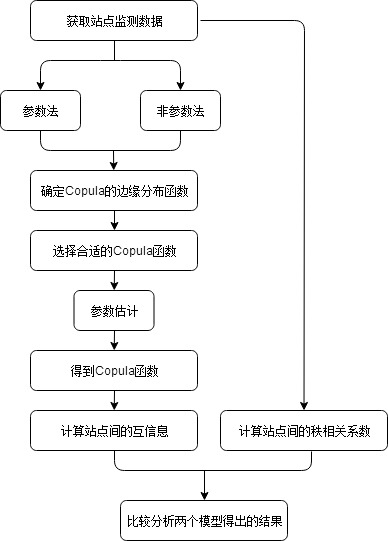
图1. 1 技术路线图
- Copula理论与互信息理论
- Copula函数
早在1959年,Sklar提出了Copula理论,他认为,一个Copula函数和k个边缘分布函数可以组成任意一个联合分布函数,并且这个Copula函数可以刻画随机变量间的相关性。到了1999年,Nelsen更为严格的定义了Copula函数:Copula函数实际就是连接随机变量的联合分布函数和各自的边缘分布连接起来的的函数。即函数,使
(2.1)
2.1.1 Copula函数的基本性质
- 对于随机变量而言,Copula函数都是递增的,也就是说,固定一个边缘分布,那么另一个边缘分布的值将会影响联合分布的值,随着它的增大而增大;
- 对于一个联合分布的发生概率而言,只要其中一个边缘分布的发生概率为0,那么它的值就为0,而如果一个边缘分布一定会发生,即其发生概率为1,那么这个联合分布的的发生概率就由其他边缘分布来决定;
- 如果随机变量间相互独立,那么其联合分布的值就是随机变量的乘积;
- 对于二元Copula函数而言,联合分布的值会因为两个边缘分布的值同时增大而增大。
Copula方法在实际应用中有很多优势。首先,Copula函数建立的多元分布是非常灵活的。而在以前,通常要规定所有的边缘分布均属于同一分布,如多元正态分布、t分布等,现如今,我们在求取多元分布时,可以通过用一个Copula函数来连接n个任意形式的边缘分布生成;其次,对于描述描述线性相关的相关系数而言,要想其值不发生改变,就要保证变量在线性变换下,但如果相关性测度和一致性是由Copula函数生成的,那么其值在严格单调增的变换下均不会发生变化,这使得Copula函数具有更大的应用范围;除此之外,在用Copula理论构建模型时,不需要一定将随机变量边缘分布和相关性结构放在一起研究。我们可以选择任意的边缘分布,且只要将变量的变化改为单调增,那么其相关性测度和一致性将不会受到影响。
2.1.2 Sklar定理
Sklar定理:令为具有边缘分布的N元联合分布函数,则存在一个Copula函数,满足
(2.2)
若是连续函数,则唯一确定;反之,若为一元分布函数,是一个Copula函数,则由式(2.2)确定的是具有边缘分布的N元联合分布函数。
在诸多的定理中,Sklar定理可谓非常重要,它可以让我们理清多维变量之间的关系是如何通过度量其边缘分布函数之间的关系来实现的,它让我们从一个非常直观的角度去理解Copula函数在处理多维变量时的问题。首先,确定的是多维变量边缘分布函数间的相关关系,并且联合分布函数是通过Copula函数连接多维变量的边缘分布函数来表达的,而这个Copula函数是一定存在的。那么多维变量的联合分布函数就可以由已知的Copula函数和边缘分布函数求得。
- Copula函数族
Copula作为联合分布函数和边缘分布函数之间的连接函数,包含了很多分布族,人们最常见的是Aechimedean分布族和椭圆分布族。正态分布函数和t分布函数均属于椭圆分布族中,Gumble Copula、Clayton Copula、Frank Copula和阿基米德Copula则隶属于Archimedean分布族。
- 正态Copula函数
N维正态(高斯)Copula分布函数和密度函数的表达式分别为
(2.3)
(2.4)
其中,是一个n阶对称正定矩阵,其对角线上的元素全为1,是矩阵的行列式;是一个n维的标准正态分布函数,其边缘分布都是标准正态分布,并且它的相关系数矩阵为;标准正态分布函数的逆函数由表示;;为单位矩阵。
N维的正态Copula函数太过复杂,我们选取二元正态Copula函数来对正态Copula函数进行分析,它的分布函数和密度函数表达式为:
(2.5)
(2.6)
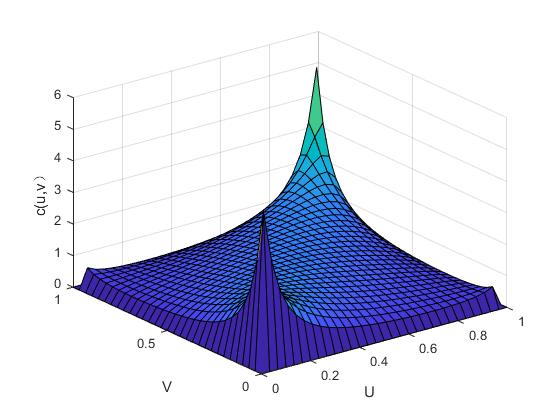
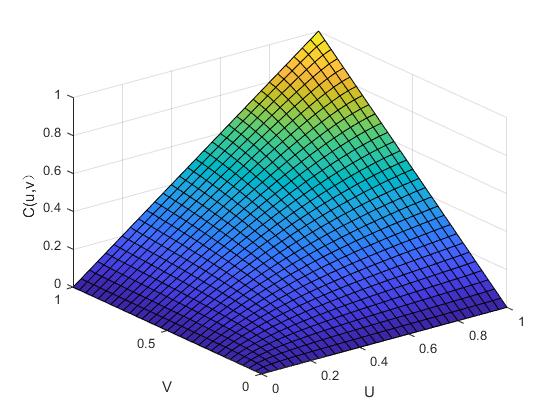
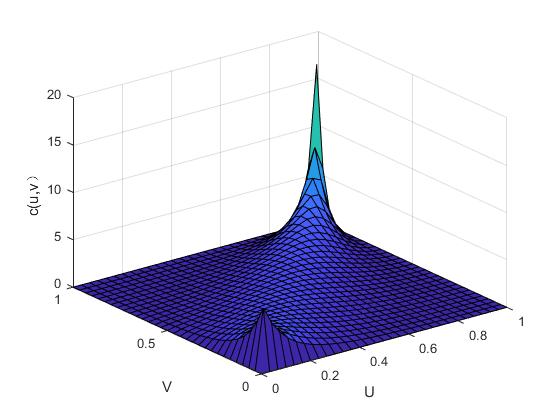
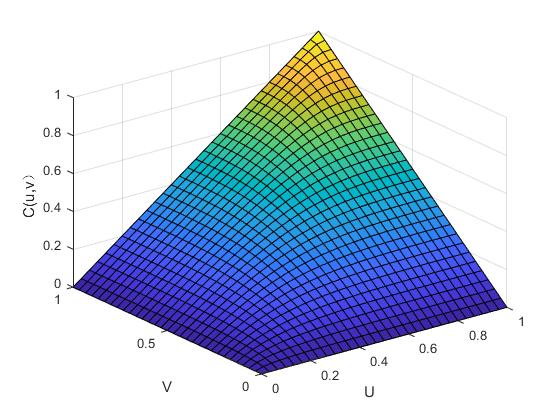
其中,函数的参数是,和的线性相关系数也是该函数,并且标准一元函数的逆函数是。图2.1与图2.2便是二元正态Copula函数的密度函数图和分布函数图,以此我们可以分析它的分布特点。
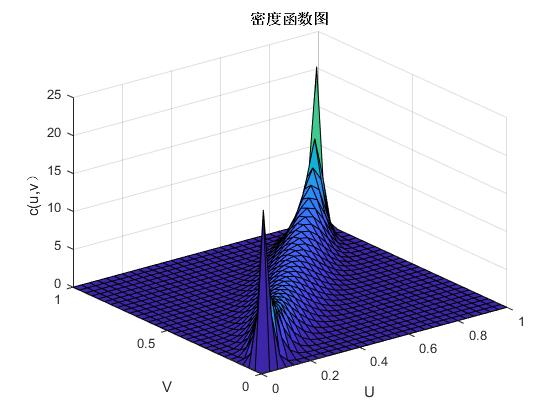
图2. 1 二元正态Copula函数的概率密度图
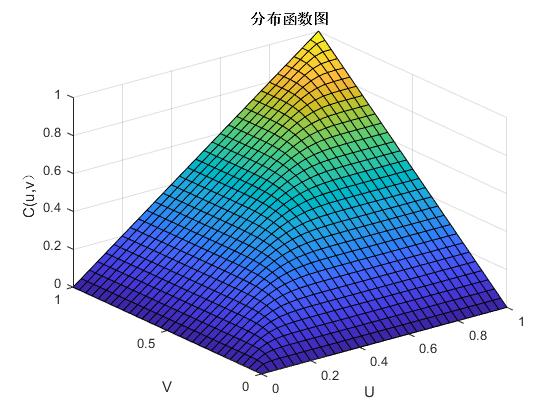
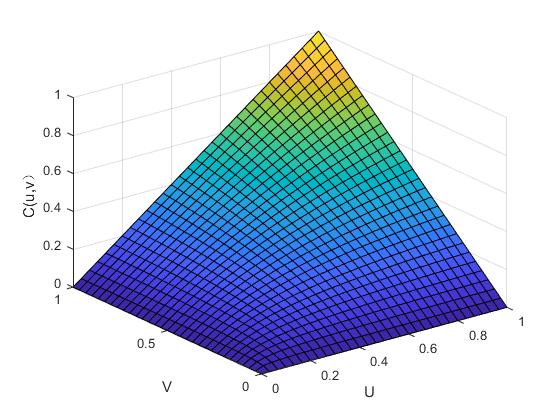
图2. 2 二元正态Copula函数的分布函数图(ρ=0.7)
依上图可得:正态Copula函数在分布上具有明显的对称性,因此,在进行相关分析时,可以考虑用正态Copula函数来拟合具有对称性的相关关系。
- t-Copula函数
N维t-Copula函数的分布函数和密度函数的表达式分别为:
(2.7)
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: