摘 要

人类所生活的世界是一个三维空间，而现今为止主流的记录媒介是二维图像。介绍了世界坐标系、摄像机坐标系、图像坐标系三者之间的转换关系。基于SFM技术，可以实现二维到三维的转变，更符合人类的认知和实际。首先对相机进行常用的相机标定，获得相机参数，通过透视畸变校正后即可得到无畸变的图像。通过研究经典的Harris、KLT、SIFT等角点检测算法得到较为精准的匹配点集，求得本质矩阵E，进而可以消除一些误匹配，最后确定匹配点的三维位置生成三维点云，进行建筑物模型的三维重建。进行各个算法效率和准确度的比较，为后续的研究提供了参考。

关键字：角点检测；立体匹配；基本矩阵；SFM算法；三维重建

Abstract

The world that human beings live in is a three-dimensional space. So far, the mainstream recording medium is two-dimensional images. The conversion relationship between the three systems of the world coordinate system, camera coordinate system and image coordinate system is introduced. Based on SFM technology, the transformation from two dimensions to three dimensions can be realized, which is more in line with human cognition and reality. First, the camera calibration is usually used to get camera parameters, and then the distortion free image can be obtained through correction of perspective distortion. By studying the classical Harris, KLT and SIFT corner detection algorithms, the accurate matching points are obtained, and the essential matrix E is obtained, and then some mismatches can be eliminated. Finally, the three-dimensional position of the matching point is determined to generate three-dimensional point cloud, and the 3D reconstruction of the building model is carried out.The efficiency and accuracy of each algorithm are compared, which can provides references for the future research.

Key Words：Corner detection；stereo matching；essential matrix；SFM algorithm;three-dimensional reconstruction

第一章 绪论

1.1 目的及意义

在人类所生活的世界里，人眼所见到的物体、自然现象等绝大多数都是以三维的形式展现的。但是直到如今，在绝大多数情况下我们却用图片、录像等非三维介质来描述记录这些事物。毫无疑问这些介质信息与人类的直观视觉的认知和习惯是不相匹配的。如今，随着计算机视觉技术的快速发展，三维模型重建技术也越来越广泛地渗透到人类的生活和工作中，比如：医疗领域，利用透视扫描，可以重建器官的实时模型，从而为病人病情的研究提供理论支持；军情领域，如果能够由战场的实时照片来重建三维地形模型，进而就可以快速实现在虚拟场景中实时指挥作战，提高军队指挥决策能力；旅游服务方面，可以将景点模拟成真实的三维场景，给旅客展示生动的风景等等。都可以利用SFM技术进行三维模型的构建。

SFM(Structure from motion)是由一系列包含着视觉运动信息（motion signals）的多幅二维图像序列(2D image sequences)估算模拟三维结构(3D model)的技术。其属于计算机视觉及可视化的研究领域。SFM通常来说，是通过一些相关的图像和其特征的一个二维集合来估算出空间点的三维坐标。这个技术结合了三维空间（结构）和相机机运动（坐标）的估算，因此称之为Structure from motion。特别是近十年来，以SFM方法为基础的三维模型重建技术为代表的新兴问题成为了计算机视觉大方向中一个非常火热的研究领域，其可以提供相对快速有效的实现三维建模，满足现实生活中各个领域的需求，为重大问题提供强有力的解决方案。因此，可以基于matlab设计一个小程序，实现基本的SFM的三维建筑物模型重建。

1.2 国内外研究现状

计算机图形学诞生于1963年，至今已经经历了近六十年的发展。目前为止，SFM经常运用在如下方面：电影制作、战场三维建模、计算机图像处理、医疗图像分析、地质测绘等。SFM总体来说还是计算机图像学的一门较新的技术，发展相较于二维图像处理可以说是小巫见大巫，只经历了仅仅几年的火热期。计算机视觉理论，通俗来讲就是用电脑来模拟人类的视觉能力，从而获取图像特征和进行图像信息处理。到目前为止，SFM技术已经取得了长足的发展。2009年，来自华盛顿大学的研究人员与微软合作使用15万张罗马图片，用SFM技术构建了一个古罗马城的模型，震惊了全世界^[1]。

就目前的发展来看，SFM技术在许多领域得到了越来越广泛的应用，为这些领域的快速发展做出了卓越的贡献。此技术已经能达到实际商业运用的标准。但目前此技术仍存在一些问题需要作为重点去研究：

（1）图片特征点检测和匹配方面，一些经典的的角点检测算法在当图像在进行变换时，比如旋转、平移和尺度缩放等情况时各不相同，速度与精度总是像鱼与熊掌的关系，不可兼得。而如今人们对三维建模的要求越发严苛，既要求速度，也更讲究精度，尤其是对于某些有高精度要求和实时性的领域（比如军事领域）来说，目前来说远未达到理想的要求。为了解决这些问题，许多人提出了兼顾两者的方案，总体可分为两类：其中之一就是对照片进行精建操作，这样就可以用尽量少的信息表现出更明显的特征，提高了处理速度；另一个方案则是获取模型的局部表面特征点^[2]，再整合图片的深度特征，就可以在局部条件下，分析图像几何特征不变性就很可能发现更好的三维特征点检测和匹配算子。

（2）SFM建模是一个多环节的技术，各个环节的联系又较为紧密，如果某个环节做得不好，会对其他环节影响很大，使得总体不确定性很大^[2]。

（3）SFM建模结果取决于特征点的精度和数量，如果特征点不能很好的表述立体模型信息，则建模效果会很差。

（4）对更深一步的稠密多视图三维模型中的应用仍处于探索阶段^[4]。可以和大规模的卫星影像和航拍影像对地面目标进行快速准确的重建，结合信息融合技术做态势评估和威胁评估，也是SFM发展的一个大方向。

1.3 基本内容及技术方案

1.3.1 研究内容

（1）SFM的算法学习

SFM算法是对二维图片处理进行三维建模，从而实现二维到三维的跨越。我们需要挑选出满足算法的图片。通过校正方法得到相机估计参数，进而得到场景几何信息及稀疏的3D点云。

（2）相机标定和三维离散点求解

根据SFM算法的要求，需要对相机进行标定处理，matlab有较方便的相机定标处理方法，只需利用相机拍摄实体场景进行棋盘定标即可^[5]，使拍摄出来的图片都符合应用要求。接着进行空间点特征匹配工作，基于经典的Harris角点匹配算法^[6]，进而可以估计出空间离散三维点的坐标，基于KLT算法的特征点跟踪，最后实现最后的建模。

（3）软件研发

Matlab有较强的数据处理计算能力和软件开发的能力，同时有简单易用、图形处理能力强大和功能丰富的应用工具箱(如信号处理工具箱、通信工具箱等) 的优点。因此完全可以基于matlab来实现SFM建模所需的各个功能，建立一个脚本完成透镜畸变校正、特征点匹配、特征点跟踪、三角化、纹理分析以及最后的建模等操作。

1.3.2 技术方案

对建筑物的各个方向录取一段视频，然后截取出符合建模要求的视图，通过相机参数可以进行特征点提取和特征点匹配在摄像机标定^[7]，研究传统的相机标定方法，制作标定模板，再通过相应的算法求单应矩阵，继而可以求得相机内部参数的矩阵，以及图像运动参数R，t。另外，照相机标定是SFM建模过程中的关键步骤，因为摄像机得到的照片往往具有枕型畸变或桶型畸变，必须对其进行修正。校正精度直接影响了空间离散三维点的估计精度，不容忽视。

空间离散点三维坐标具体流程如下：

1.模型粗建：根据建筑物的两幅正视图和侧视图生成纹理图像，重建建筑物模型。

2.特征点提取和特征点匹配：根据已知的特征点，运用建筑结构的规律即可推导出更多的匹配点。

3.SFM的算法研究：理解SFM算法的原理，并检查各个方面参数是否符合算法要求。

4.SFM的模型构建：计算外参矩阵（即旋转及平移矩阵R和t），由此便可估算出特征点的三维位置。

5.插值：由密集的三维点可以生成三维网，从而得到三维模型。

6.三维模型精建：由多分辨率图像拼接算法，生成纹理图像，然后将其映射到三维模型上，从而增强建筑物模型真实感。

7.软件实现：根据算法要求，在matlab中实现各个功能并设计出一个界面友好的程序，分步实现各个功能。

下图1.1所示是工作流程图:

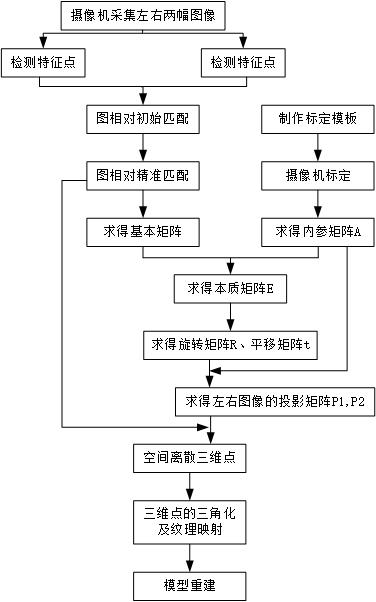
图1.1 SFM工作流程

第二章 图像三维建模理论基础

对采集到的图像或视频进行处理，获得相应的实际物体或场景的三维信息，通常称这样的技术为计算机视觉。计算机视觉理论涉及到许多方面，主要如下：射影几何、对极几何以及摄像机模型等^[9]。

2.1 摄像机模型

摄像机的成像过程是物体由三维空间投影到二维平面的过程，属于立体视觉范畴^[10]。要想确定空间三维点与二维图像的关系，必须先确定摄像机模型参数。

2.1.1 三个坐标系之间的关系

与立体视觉相关的三种坐标系为：图像坐标系、世界坐标系、相机坐标系。

第一个是图像坐标系。二维图像存储于计算机中的形式可以用二维数组M×N来表达，M行N列的每一个最小单元称为像素点（pixel），每一个点都有一个亮度，通常被称为灰度。由此，可以建立一个直角坐标系u-v，该坐标系以像素为单位，但却无法表示出坐标点的具体位置。因此，可以构建一个图像坐标系x-y，设定单位为物理单位（如㎜），其中两坐标系轴相互平行（如图2.1）。

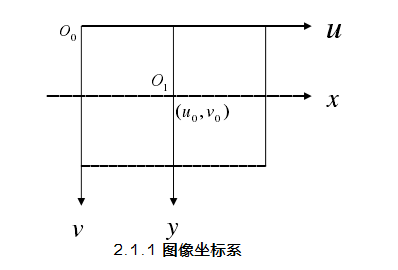
图2.1 图像坐标系

设每个像素点在x,y轴的物理尺寸为dx，dy，O1为图像平面与照相机光轴的交点，则不难得出如下式变换关系：

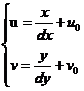（2.1）

可以用齐次坐标和矩阵形式表示上式，由此可以得到如下关系：

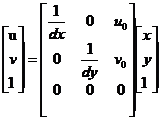（2.2）

第二个是摄像机坐标系，如图2.2，O为照相机的光心，XC轴与x轴平行，Yc轴与y轴平行，Zc轴垂直于图像平面，为照相机的光轴。图中，空间中的点P与摄像机光心O的连线相交平面xy于p点，由此，图像坐标系与摄像机坐标系两者之间的关系可表示为如下联合方程：

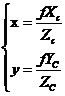（2.3）

其中，在摄像机坐标系下，Xc，Yc,Zc为空间点P的非齐次坐标，f为摄像机焦距。将其用矩阵形式和齐次坐标表示出来为：

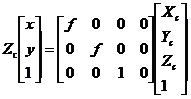（2.4）

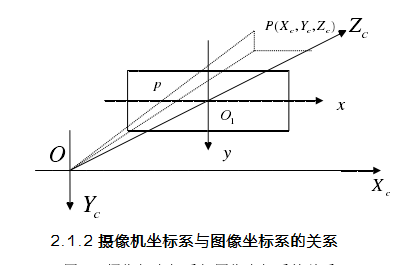
图2.2 摄像机坐标系与图像坐标系的关系

第三个是世界坐标系。摄像机是在三维场景中。因此，需要一个能描述场景中物体位置信息的坐标系，通常其由三个轴组成。设空间中一点P的齐次坐标为（X_w,Y_w,Z_w,1）^T表示在世界坐标系下的坐标，（Xc,Yc,Zc,1）^T表示在照相机坐标系下的坐标，则有如下变换关系：

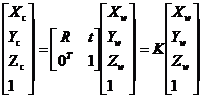（2.5）

上式中，R称为旋转矩阵，t称为平移向量，0T为（0，0，0）T,K为4*4的矩阵。

2.1.2 三个坐标系之间的变换

由上各个结论式，可以得到世界坐标系和图像坐标系的转换公式:

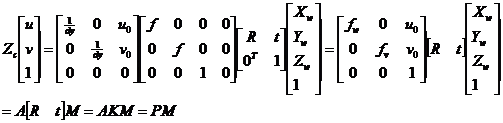（2.6）

上式中，A为3×3矩阵，fw、fv、u0、v0是摄像机内部参数，其中A被称为摄像机内参矩阵，K称为摄像机外参矩阵，P称为投影矩阵，M为P点在世界坐标系下的齐次坐标。

如图2.3表示出的是三个坐标系之间的变换关系：

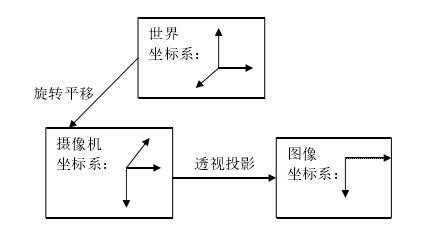
图2.3 三个坐标系的转换关系

2.2 视图间的几何关系

对极几何是三维重建的基本理论，描述了同一相机在不同位置拍摄同一物体而得到的两幅图像必然满足某种几何约束。可以用基本矩阵F来描述对极几何关系^[11]。因此，精准估算基本矩阵F得到精准点集，对三维建模具有极为重要的意义。

2.2.1 对极几何

如图，I，I’,C为左视点的光心，C’为右视点的光心，空间点P在I,I’上的成像为m,m’。CC’与I,I’分别交与e,e’点，称为极点，图像平面通过其的点为极线^[12]。

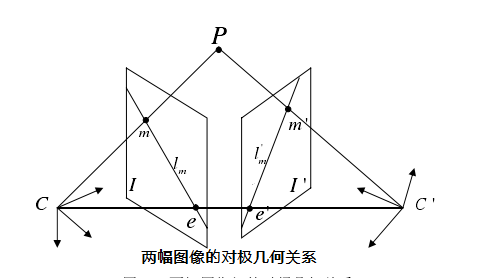
图2.4 两幅图像的对极几何关系

对极几何的约束关系可表示如下：对平面I上的任一点m，m的匹配点m’必定在极线lm’上；反之，对平面I’上任一点m’，m’的匹配点必定在极线lm上。

2.2.2 基本矩阵

由于两幅图像存在的对极几何关系，可以用基本矩阵F来表示这种关系，存在L=Fm由任一点m的匹配点m’必定在极线lm’上,则有m’Fm=0,其中，基本矩阵三项重要性质如下：

（1）当矩阵F同时满足m’Fm=0且矩阵的秩为2，则称F为基本矩阵

（2）极点e,e’满足Fe=0,Fe’=0

（3）若相差一个非零常数因子，基本矩阵F是唯一的

2.2.3 单应矩阵

如图，点x与光心C的连线并延长与世界平面π交于点xπ，另一个图像上的投影点为x’，从点x到点x’的映射是由平面π诱导的单应。则存在x=H1πxπ，x’=H2πxπ,那么这两个透视变换的复合就构成了两个图像之间的单应H，x’=H2πxπ=H2πH1π-1x=Hx。因为不知道空间平面坐标之间的关系，可以通过两幅图像中的匹配点对来确定单应矩阵。

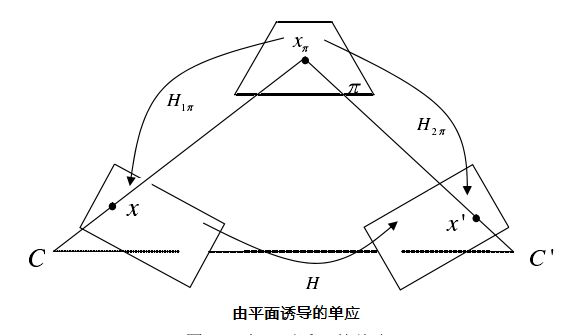
图2.5 由平面诱导的单应

特征点的检测和匹配

由于图像往往比较复杂，要想每个像素都处理到比较困难，因此可以提取一些比较有代表性的特征点来进行处理。特征点的提取和匹配的精度对于三维建模是至关重要的，主要要求两点：1.特征点数量足够多。2.特征点精度高。

3.1 特征点提取方法

特征点反映在图像中指的是灰度变化剧烈的像素点，可以类比为桌子的角、两只牙签的相交点、弯道上的拐点和单个分布的点等都可以作为特征点。

角点检测的方式各不相同，但总体来说可以将角点检测算法分为两类：基于图像边缘的角点检测算法和基于图像灰度的角点检测算法。其中，基于图像边缘的算法非常依赖于边缘提取算法，而基于图像灰度的角点提取算法是检测出局部范围的灰度变化极大值点，不再需要边缘提取，并且精度也有一定保障，所以这类方法广泛应用于实际应用中。

常用的角点检测算法有如下几种：

（1）Harris角点检测算子：1988年，C. Harris和J. Stephens^[13]提出了基于图像灰度梯度的经典Harris角点检测算子.Harris角点检测算子是对Moravec算法的改进，虽然后者算法简单，但运行速度慢且误检测率高。两者的基本思想是相似的，都是建立一个特定大小的移动窗口来检测窗口内的变化，进而检测出角点。如图3.1所示，当窗口在图像上移动时，总体来说只会出现如下三种情况：

1.非角点区域：窗口内像素点的灰度值在水平和垂直方向移动时变化都不会太大；

2.图形边缘区域，窗口内像素点的灰度值在水平或者垂直方向（单个方向）上变化较大；

3.角点区域：窗口内像素点的灰度值在水平和垂直方向上都会有较大变化。

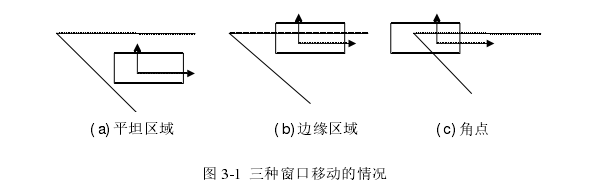
图3.1 三种窗口移动的情况

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：