摘 要

本文收集了1918年至2018年全球7级以上地震灾害数据，通过R语言对地震灾害数据进行空间点模式分析，从不同角度探索全球地震灾害点的空间分布模式与聚集状态。在确定地震灾害的聚集特征后，基于K-means算法的空间聚类分析方法对全球地震灾难进行聚类分析，从而进行地震集群探索，挖掘全球地震灾害空间分布的聚类特征。论文研究结果表明：全球7级以上地震灾害的空间分布模式具有聚集性且在不同空间尺度上的聚集趋势存在差异性：在0到200000米的最近邻范围内，地震灾害空间聚集特征最为明显；而在200000到700000米的最近邻区间内，地震灾害的空间聚集效应有所衰减。全球7级以上地震灾害可划分为6类，具有震级和地震深度的相对低值聚集特征的地震灾害主要分布于北美板块和亚欧板块东西边界处以及澳大利亚板块东部边界处；而具有震级和地震深度的相对高值聚集特征的地震灾害则分布较为分散，但主要位于环太平洋火山地震带上。

关键词：全球地震；空间点模式；聚类分析；R语言；GIS

Abstract

This paper collects the global earthquake disaster data of magnitude 7 or above from 1918 to 2018, and uses R language to analyze the spatial point pattern of earthquake disaster data. The spatial distribution pattern and aggregation state of the global earthquake disaster points are explored from different aspects. After determining the clustering characteristics of earthquake disasters, the spatial clustering analysis method based on K-means algorithm is used to cluster global earthquake disasters, so as to explore global earthquake disasters clusters and exploit the clustering characteristics of the spatial distribution. The research results of this paper show that the spatial distribution pattern of global earthquake disasters with magnitude 7 or above is aggregated. The agglomeration trend of global earthquake disasters with magnitude 7 or above had variation at different scales. In the nearest neighborhood of 0-200,000 m, the spatial clustering characteristics of global earthquake disasters with magnitude 7 or above are most obvious, while in the nearest neighborhood of 200,000-700,000m, the spatial concentration effects of global earthquake disasters are attenuated. The global earthquake disasters with magnitude above 7 can be divided into 6 clusters. The earthquake disasters with relative low-value clustered characteristics of magnitude and depth are mainly distributed at the eastern and western boundaries of the North American plate and the Eurasian plate, the eastern boundaries of the Australian plate. However, Earthquake disasters with relative high-value clustered characteristics of magnitude and depth are relatively scattered, but most earthquake disasters mainly located in the Pacific Ring of Fire.

Key Words：Global Earthquakes; Spatial Point Pattern Analysis; Clustering Analysis; R Language; GIS

目 录

第1章 绪论 1

1.1 研究背景 1

1.2 国内外研究现况 1

1.3.1 国外研究现况 2

1.3.2 国内研究现况 2

1.3 研究内容与技术路线 2

1.4 论文组织结构 4

第2章 研究理论及方法 5

2.1 空间点模式分析方法 5

2.2.1 G函数法 5

2.2.2 F函数法 6

2.2.3 J函数法 6

2.2 空间聚类分析方法 7

2.2.1 空间聚类分析 7

2.2.2 K-means算法 8

2.3 R语言与空间分析 8

第三章 基于点模式的全球地震灾害的空间分布分析 10

3.1 数据来源 10

3.2 数据预处理 10

3.3 基于G函数法的全球地震灾害分析 11

3.4 基于F函数法的全球地震灾害分析 13

3.5 基于J函数法的全球地震灾害分析 14

3.6 小结 16

第4章 基于空间聚类的全球地震灾害分析 17

4.1 聚类预处理 17

4.2 基于K-means算法的全球地震灾害聚类分析 17

4.3 小结 20

第5章 总结与展望 21

5.1 总结 21

5.2 不足与展望 21

参考文献 23

致 谢 24

第1章 绪论

研究背景

地震是发生在地球表面的震动，是由于地壳的能量突然释放并且产生地震波的自然现象。地震的大小可以小至人无法感觉，亦可以大至足以摧毁整个城市。地震灾害则是指由地震引起的直接灾害和次生灾害，具有突发性较强，破坏性较大，社会影响深远，防御难度大，产生次生灾害和持续时间较强等特点。地震灾害的影响包括但不限于震动和地面破裂位移、山体滑坡、土壤液化、火灾、海啸、洪水以及对人类的居住环境（包括道路、桥梁、建筑）和生命财产的伤害。

根据现有仪器的探测数据进行估计，每年大约发生50万次地震，其中大约有10万次可以直接被人感觉。历史上最具破坏性的地震之一是1556年1月23日发生在中国陕西省的陕西地震，超过83万人在此次地震中死亡。该地区的大多数房屋都是位于黄土山坡的窑洞民居，窑洞倒塌导致遇难者丧失生命。1976年唐山大地震是20世纪最致命的一次地震灾害，造成24万至65万人的死亡。智利1960年的地震是在地震仪上测得的最大的地震，震级达到9.5级，震中位于智利的卡埃特附近。地震灾害发生在靠近人口稠密的沿海地区时在往往会造成海啸，从而摧毁数千公里以外的社区；而最有可能造成重大生命损失的地区包括地震相对稀少但强度较大的地区，以及地震建筑规范松散、规划不合理的贫困地区。

威力巨大的地震灾害给人类社会带来了严重的损失，它不仅威胁到人类的生命财产安全以及社会经济发展，也对社会生产和城市化进程产生了重大影响。地震是人类目前面临的威胁最大的自然灾害之一,对它的分析和研究一直以来深受学者们的重视^[1]。由此，对于地震灾害的相关探索与研究，如地震目录的完整性分析、地震时间的统计分布分析、地震的空间丛集分析、余震危险性分析等研究工作成为许多学者的关注重点。其中，对于地震灾害统计研究和空间聚集研究一直是地震研究的基础性工作之一，通过分析地震目录所得的地震灾害空间分布特征和空间聚集规律可直观反映地震发生趋势和影响区域，有助于地震灾害预警、提升灾情应对能力和地震灾害深入研究的展开。

1. 国内外研究现况

近年来，国内外研究人员从不同角度采用了不同的研究方法针对地震灾害的时空分布模式作了大量研究，涉及时间统计研究、空间点模式研究和空间分布研究等诸多研究方法，取得了不少成效，也为地震灾害的预警、应对以及进一步研究提供了具有重要意义的参考。

1. 国外研究现况

地震的时间分布遵循离散的泊松分布，其时间在时间上是独立的，这一假说在地震研究上被广泛接受。围绕这一主题，国内外学者也进行了大量的分析和研究。Sr-dan Kostic等应用非线性时间序列分析方法对塞尔维亚1970年至2011年间地震震级时间分布的潜在模式进行研究，验证了塞尔维亚1970年至2011年间地震震级的随机分布^[2]。Yosihiko Ogata在对地震发生的时空点过程模型研究过程中，同样认为地震的发生在时间的分布上符合泊松分布，其中余震活动符合非平稳过程的泊松分布^[3]。由此，可以认为地震的发生时间是随机且难以预测的。

关于地震的空间分布，其研究亦十分丰富，Sanja Scitovski考虑了将基于密度的聚类算法Rough-DBSCAN应用于地震区划的可能性^[4]； Yosihiko Ogata采用点过程残差分析法进行了余震空间分布的模型研究；Y. Y. Kagan等探索了不同分支模型在地震聚类分区的应用^[5]。其主要的研究方向还是在地震分区上，通过对地震的时空数据进行聚类分析从而划分地震区，可以有效地为地区建设和防震规划提供数据参考，从而提升地震灾情的应对效率与能力。

1. 国内研究现况

国内的地震灾害空间分布模式分析亦讨论颇多，运用的分析方法也各有特色。高冬艳将地理信息系统与空间点模式的研究方法进行结合，运用G、F、J、K、L等多种距离函数进行点模式分析并进行对比，从多角度研究了云南地区地震的空间分布的描述性统计特征与空间点模式^[6]；徐伟进在2012年研究了地震空间丛集特征和空间点分布模式，并且在2016年应用Neyman-Scott（Archibald，1984）空间丛集过程及相似的点过程模型检验了地震空间分布模型^{[7] [8]}；郑文峰等（2015年）借助现有空间点模式分析方法进行描述强震与非强震之间特性的空间相关性方法探索^[9]；李思颖则基于Moran’s I指数等空间分析的方法对地震数据进行研究^[10]……国内关于地震的空间分布研究主要的研究方向还是地震灾害的空间点模式研究，以及地震灾害的时空描述性统计分析和通过对地震灾害进行聚类分析探索地震灾害的聚集特征。

1. 研究内容与技术路线

综上所述，对地震灾害的空间分布模式和聚集特征展开研究具有重要的现实性意义。地震的大小通过震级衡量，其中7级以上（包含7级）的地震被称为强震，对人类生命和社会安全存在更大的威胁。地震灾害可以抽象为地理空间上的点状“事件”，因此可以采用空间点模式分析方法对地震灾害的空间分布模式和集聚特征进行定量研究^[11]。而在确定地震灾害的聚集特征基础上，对地震灾害进行聚类分析，可以更好地探索地震灾害的内在聚集结构，对发现潜在的地震集群，挖掘地震丛集规律十分有效^[12]。

地震灾害数据经过统一整理后被称为地震目录，通过地震目录我们可以获取直观而准确的地震发生时间信息、经纬度和地名等震中位置信息、深度和震级等强度信息甚至地震灾害导致的人员伤亡、财产损失等相关信息。早期的地震相关参数一般依据历史文献记载进行估计，也称作历史地震目录；进入现代后，现代地震参数根据地震仪记录数据得出，所得地震参数较历史地震精确、丰富。地震目录是进行地震灾害相关分析的基础性研究资料。

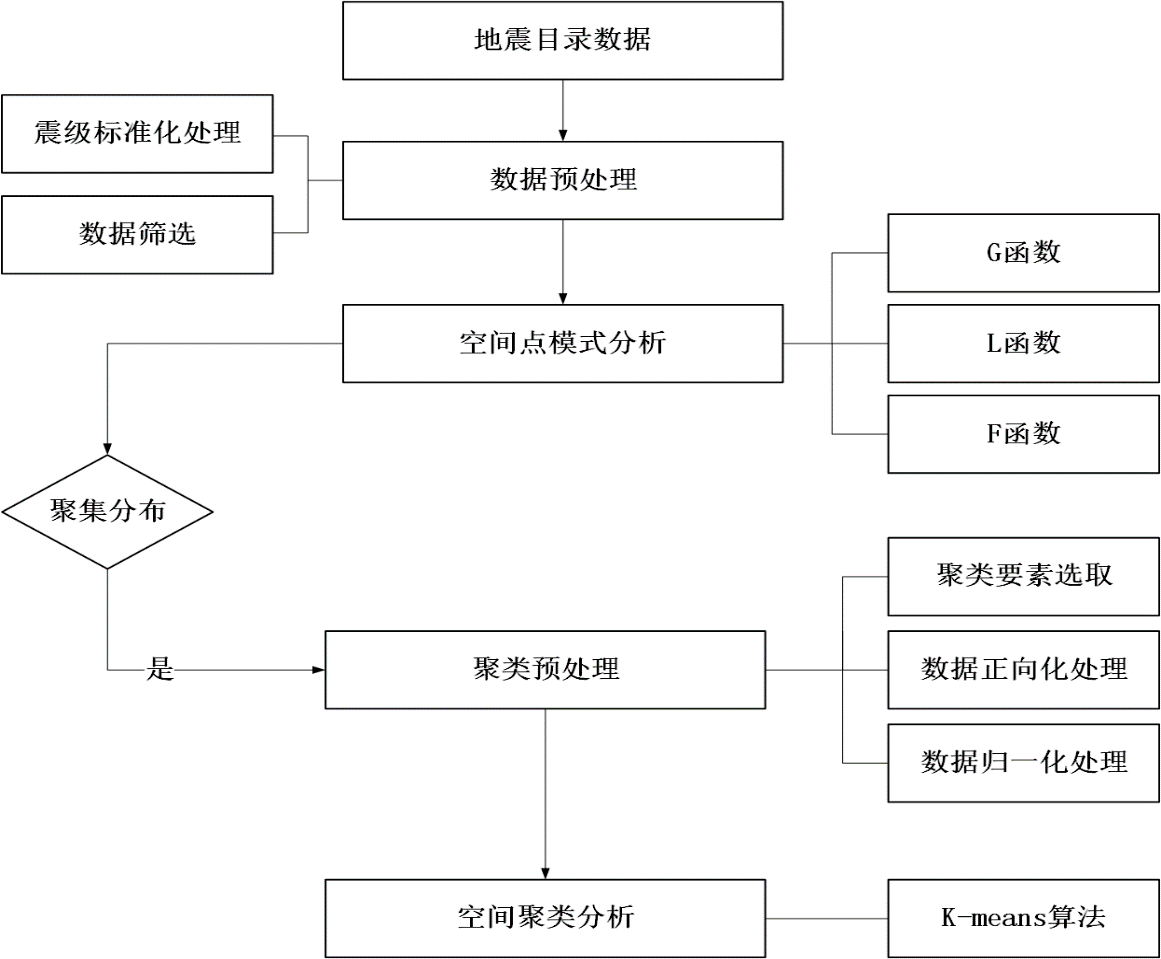本论文在此背景下，收集100年来全球地震灾害统计数据和地震震中点数据等地震目录数据，进行数据标准化处理和筛选以确保分析数据有效性，减少分析误差。通过R语言对地震灾害数据进行空间点模式分析，具体分别运用基于G函数、F函数和L函数的空间点模式分析方法进行对比研究，从不同角度探索全球地震灾害点的空间分布模式与聚集状态。在确定地震灾害的聚集特征后，基于K-means算法的空间聚类分析方法对全球地震灾难进行聚类分析，运用ArcGIS软件进行聚类结果可视化，从而进行地震集群探索，挖掘全球地震灾害空间分布的聚类特征。

图2.1 全球地震灾害研究技术路线图

地震灾害作为一种与地理空间紧密联系且分布具备一定规律的灾害，使用ArcGIS等平台软件进行分析的研究较多，而结合R语言和GIS技术进行分析的研究较少。而地震目录作为地震灾害的基础性资料，统计了较为完备的地震灾害空间和属性信息，并且数据规模较大。本文基于R语言与GIS技术对100年来7级以上的强震灾害展开分析，将GIS的空间分析优势与R语言在大规模数据集处理上的优势相结合，不仅能够很好地研究地震灾害的空间属性，而且可以快速、准确地进行全球地震灾害的研究，同时也为地震灾害的空间分布探索提供了新的研究思路，为地震灾害的深入研究提供了新的研究模式作为参考。

1. 论文组织结构

基于空间点模式以及聚类分析对全球地震灾害展开研究，本文分为五个章节展开，各章的主要内容如下：

第一章，对全球地震灾害的研究背景进行描述，从而展开本文的主要研究内容并讨论进行全球地震灾害空间分布研究和聚类分析研究的意义，并参考了国内外的研究现况，最后对文章的结构进行概括。

第二章，对相关理论和研究方法进行描述，包括空间点模式的概念以及分析算法、聚类分析的基础理论与算法以及R语言与空间分析的相关算法。

第三章，简要介绍了本文分析的100年间全球7级以上地震灾害数据来源与情况，并描述了数据预处理流程，再基于R语言分别运用G函数、F函数和L函数算法对全球地震灾害进行点模式分析，研究其空间聚集趋势及分布模式。

第四章，在第三章的研究基础上对全球地震灾害进行聚类分析，首先进行聚类的数据预处理和聚类数目确定，然后基于K-means算法对100年间全球地震灾害进行聚类分析，探索地震灾害的潜在分布集群与聚类特征。

第五章，对本文的研究内容和结果进行总结概括，对研究存在的不足之处进行反思，并对未来的研究方向进行了展望。

第2章 研究理论及方法

地震灾害可以抽象为一系列包含多类属性的点数据，而空间点模式分析和空间聚类分析研究均可基于点数据展开。通过空间点模式分析，可以识别全球地震灾害的分布特征是随机分布、均匀分布还是聚集分布。而通过空间聚类分析，则可以对具有聚集分布特征的地震灾害点进行划分，从而探索地震灾害的聚类特征和潜在集群。

空间点模式分析方法

空间点模式分析是对一定研究范围内一系列空间点的聚集程度展开研究。虽然空间点的分布存在多种情况，但一般都区分为3类，即均匀分布、聚集分布和随机分布。如图2.1所示，分别展示了空间点的三种分布模式。仅从统计学角度进行分析，地图上空间点的分布可以是任意模式，但考虑到空间点自身的位置属性，空间点有可能存在聚集的特性。研究空间点数据的聚集性对于深入理解地理现象的特征具有重要意义^[13]。

图2.1 空间点分布模式

空间点模式分析主要从定量的角度对空间数据的聚集或分散程度进行度量，其分析方法主要可以分为三类：基于密度（聚集性）的方法，如样方法与核密度估计法；基于距离（分散性）的方法，如J函数法、F函数法、G函数法等；研究专题属性的空间点聚类趋势分析，如Moran’s I指数法等^[14]。在进行地震灾害的空间点分布模式分析时，学者们大多使用ArcGIS等软件平台提供的基于核密度估计、Reply’s K函数与L函数以及基于G指数的热点分析方法进行研究，本文通过使用R语言进行编程实现ArcGIS等软件平台未实现的点模式分析方法即G函数法、F函数法和J函数法对1918至2018年全球7级以上地震灾害进行研究，从不同角度对全球地震灾害的空间点模式特征进行更深层次的挖掘。

1. G函数法

G函数法是一种采用最近邻距离的概率分布特征来对空间点模式的分布特征进行描述的方法。最近邻距离函数G从任意形状的窗口范围内的点分布模式进行最近邻距离累计频率函数G(r)估计，G(r)可表达为：

（2.1）

其中，s_i表示研究窗口内的一个点事件，N为研究窗口内点事件的总数量，r为最近邻距离，则表示距离小于r的最邻近点的计数。

G(r)的取值范围在[0,1]之间。若点事件的空间分布趋向于聚集模式，那么最近邻距离r较小的点的数量较多，G(r)的值在较短距离内会急剧上升；若点事件的空间分布表现为均匀分布，则G(r)的值则会缓慢增长。

G函数的显著性评价可以采用蒙特卡洛随机模拟检验的方法进行，此方法需要对次数为m的随机模拟中G函数的上界U(r)和下界L(r)计算：

（2.2）