基于群体智能算法的水位流量关系拟合毕业论文
2020-02-15 22:44:27
摘 要
水位流量关系反映了河流流量与水位之间的对应状态,二者呈现出明显的非线性相关关系。水位流量关系拟合的研究,对水文监测、水资源优化配置等领域有着重要的指导意义。在水位流量关系的研究中,主要是针对水位站提供的水位与流量的实测数据进行分析、处理,而传统的水位流量关系拟合方法是存在局限性的。
本文在分析国内外研究现状的基础上,在基本粒子群算法的基础上,提出了线性递减惯性权重和非线性递减惯性权重两种改进策略,经过分析验证,后者具有更强的寻优性能和搜索能力。以长江中游枝城水文站的实测数据为基础,将改进的粒子群算法运用于水位流量关系的拟合,并与传统的最小二乘法拟合进行对比,实验结果证明了改进的粒子群算法的有效性,具有较高的求解精度和较好的拟合效果,为提高水位流量关系拟合精度提供了借鉴和参考。
关键词:水位流量关系;粒子群算法;曲线拟合;参数估计
Abstract
The relationship between water level and discharge reflects the corresponding state between river discharge and water level, and they show an obvious nonlinear correlation. The study of water level and discharge relation fitting has important guiding significance to the fields of hydrologic monitoring and optimal allocation of water resources. In the study of water level discharge relation, it mainly analyzes and processes the measured data of water level and discharge provided by water station, but the traditional method of fitting water level discharge relation is limited.
Based on the analysis of the research status at home and abroad and the basic particle swarm optimization algorithm, two improved strategies of linear decreasing inertia weight and nonlinear decreasing inertia weight are proposed in this paper. To ZhiCheng hydrological station in the middle reach of Yangtze river, on the basis of the measured data will be improved particle swarm algorithm used in fitting of the relationship between water flow, and comparing with the conventional least square fitting, the experimental results show the effectiveness of the improved particle swarm optimization (PSO) algorithm, has high precision and good fitting effect, to improve the relationship between water flow fitting accuracy to provide the reference.
Key Words:Relationship of water level and discharge; Particle swarm optimization; Curve fitting; Parameter estimation
目 录
摘 要 I
Abstract II
第1章 绪论 1
1.1 研究背景和意义 1
1.2 国内外研究现状 1
1.2.1 国外研究现状 1
1.2.2 国内研究现状 2
1.3 研究内容 2
1.4 技术路线 3
第2章 研究区概况与数据来源 4
2.1 研究区概况 4
2.2 数据来源 4
第3章 改进的粒子群算法 5
3.1 群体智能算法 5
3.2 粒子群算法概述 5
3.3 粒子群算法原理 5
3.3.1 基本粒子群算法的数学描述 6
3.3.2 基本粒子群算法的步骤和流程 7
3.4 粒子群算法参数的经验设置 7
3.5 基于惯性权重的改进策略分析 8
3.5.1 线性递减惯性权重策略 9
3.5.2 非线性递减惯性权重策略 9
3.5.3 改进粒子群算法的流程 10
3.6 算法验证 10
3.6.1 验证方法 10
3.6.2 验证结果 10
第4章 基于粒子群算法的水位流量关系拟合 13
4.1 水位流量关系拟合 13
4.2 实例应用 13
4.3 对比分析 14
第5章 总结与展望 16
5.1 总结 16
5.2 展望 16
参考文献 17
致谢 19
第1章 绪论
1.1 研究背景和意义
水位流量关系是明显的非线性相关关系,反映的是河流流量与水位之间的相互对应状态。大多情况下,由于测量技术复杂、危险、成本昂贵等原因,河流流量的长时间序列的测量、监测难以进行,而水位信息却可以很容易地实现连续观测,因此,可以通过水位和流量之间的关系特征,将连续的水位信息,转换为连续的流量信息;有时,也需要根据流量数据反向推导出水位信息,进行河流防汛水位的设定等工作;水位流量关系拟合的研究,对于水文监测、水资源优化配置等领域有着重要的指导意义。
在水位和流量之间关系的研究中,主要是针对水位站提供的水位与流量的实测数据进行分析、处理,需要利用回归分析的方法,而传统的回归分析方法是存在局限性的。绝大多数的实际问题实质上都是非线性的,水位与流量的关系同样表现为强烈的非线性关系。但是,过去对非线性问题没有有效的拟合方法,只能转换成近似的线性模型进行线性拟合,得到的拟合效果往往很不理想。因此,如何提高水位流量关系拟合的精度一直是水资源水文领域的研究重点。
本文将粒子群算法这一群体智能算法运用到水位流量关系曲线的拟合。粒子群算法是学者们观察研究鸟群觅食行为这一群体智能而提出的。其作为一种智能寻优算法,在参数拟合、函数寻优领域有着独特的优势,得到了广泛的研究和应用。但是,基本的粒子群算法也存在不足,在求解问题的过程中,很容易陷入局部最优的状况,无法向其他区域进行更加全面地搜索,全局搜索能力和局部寻优能力很难得到一个很好的平衡。本文提出基于惯性权重的改进策略,将改进的粒子群算法应用到水位流量关系的拟合,以长江中游枝城水位站的实测数据为基础,完成水位流量关系曲线的参数拟合,并对拟合精度进行对比分析。
1.2 国内外研究现状
1.2.1 国外研究现状
在水位流量关系拟合这一领域,国外学者的研究相对较早。C.VENETIS(1970)[1]对水位流量数据取对数之后,通过在绘图纸上描点,将二者关系近似为对数关系,利用最小二乘法,结合绘图纸上直线的位置和斜率估计对数关系的参数。E.A.Zarzer(1987)[2]在非线性最小二乘法的基础上,从定义域细分的角度提出了优化水位流量关系拟合曲线的策略。KEVIN D.GAWNE(1994)[3]等学者在线性回归建模技术的基础上,引入了幂函数和Box-Cox变换来实现数据的线性,实现了基于水位流量关系曲线的决策支持计算机系统。S.K.Jain和D.Chalisgaonkar(2000)[4]将人工神经网络用于水位流量关系拟合中,与传统方法相比具有更好的拟合效果。B.Bhattacharya,和D.P.Solomatine(2005)[5]引入机器学习的方法,利用人工神经网络和M5模型树构建模型,拟合的准确性和精度都优于传统模型。Hazi Mohammad Azamathulla(2011)[6]等学者在遗传算法的基础上,运用基因表达式编程GEP拟合水位流量关系,获得了更好的拟合性能。Adrien Paris(2016)[7]等学者以亚马逊河流域为研究对象,运用卫星测高仪等技术手段,将遥感和流域模型协同应用,获得了更高精度的水位流量关系曲线。
1.2.2 国内研究现状
国内在水位流量关系拟合这一领域相对比较落后,认识到水位流量关系拟合在水资源配置、水文预测等方面的重要性之后,国内相关研究不断增大,取了许多成果。广东省水文总站黄启鸿(1988)[8]引入浮动多项式和最小二乘法,对福建水口站的水位流量关系进行了拟合,在中、高水位得到了较高的精度。湖南省水文总站罗光兰(1992)[9]在正交多项式簇的基础上进行数学推导,应用湖南4个水文站的实测资料进行了研究,拟合精度达到实用要求。徐德龙(1999)[10]将水位流量的幂指数关系取对数进行线性化,对拟合参数利用牛顿法进行优化修正,提高了拟合精度。随着群体智能算法的普及,越来越多的学者将群体智能算法应用到水位流量关系的拟合,如杨晓华(2002)[11]等学者运用自适应加速遗传算法、舒栋才(2004)[12]等学者运用免疫进化算法、詹士昌(2005)[13]等学者运用蚁群算法、汪嘉杨(2006)[14]等学者运用混合禁忌搜索算法、刘晋(2008)[15]等学者运用粒子群算法、施秋红(2010)[16]等学者运用了人工鱼群算法、吴光琼(2016)[17]运用了群居蜘蛛算法。将群体智能算法运用在水位流量关系拟合中,使得拟合参数得到了优化,提高了拟合精度。学者们根据实际还提出了许多改进算法,有的学者还结合前沿的神经网络技术,在水位流量关系拟合中都取得了很好的效果。
1.3 研究内容
明确水位流量关系的概念,阐述提高水位流量关系拟合精度的意义;阐述用于拟合水位流量关系的传统方法及流程,分析其不足之处;引入群体智能算法,阐述群体智能算法的概念、出现的背景以及常见的群体智能算法。
基于基本粒子群算法,提出改进策略,对改进算法进行验证,选择较优的改进策略。针对水位流量关系拟合精度不高的问题,收集长江中下游水位流量数据,将改进的粒子群算法运用到水位流量关系的拟合,并与传统的最小二乘法拟合进行对比,评价改进粒子群算法的拟合效果,为提高水位流量关系拟合精度提供参考。
1.4 技术路线
技术方案流程如图1.1所示,阐述粒子群算法产生的背景和研究现状,详细分析基本粒子群算法的原理,阐述算法流程,明确粒子群算法参数的经验设置及其作用;在基本粒子群算法的基础上,针对其不足,对惯性权重因子进行改进,提出两种基于惯性权重的改进策略,得到改进后的粒子群算法。
选取几种代表性的标准模型,对两种改进后的粒子群算法进行验证,两种改进策略的区别在于惯性权重随迭代次数而减小的过程是否是线性的,评价两种算法的寻优速度和拟合精度。对改进后的粒子群算法进行评价,阐述其改 进效果。
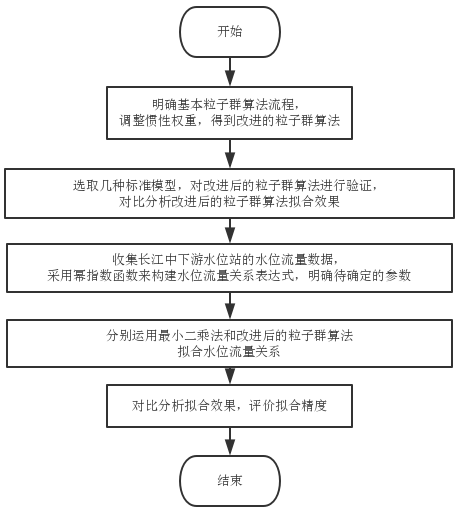 收集长江中下游水位站的水位流量数据,构建水位流量关系表达式,明确待确定的参数。分别运用最小二乘法和改进后的粒子群算法进行水位流量关系进行拟合,对比分析拟合效果,评价拟合精度,为相关水位流量关系拟合提供参考,有利于水文监测、水资源管理、水资源优化配置等方面的应用。
收集长江中下游水位站的水位流量数据,构建水位流量关系表达式,明确待确定的参数。分别运用最小二乘法和改进后的粒子群算法进行水位流量关系进行拟合,对比分析拟合效果,评价拟合精度,为相关水位流量关系拟合提供参考,有利于水文监测、水资源管理、水资源优化配置等方面的应用。
图1.1 技术方案流程图
第2章 研究区概况与数据来源
2.1 研究区概况
长江中下游地区位于东经111°~123°,北纬27°~34°,地势平缓,由长江延伸出的天然水系众多,人工修建的河渠不计其数,河网密集程度居全国之最。长江中下游地区湖泊众多,包括小湖泊在内的总数可达上万个,天然具有调节水量、延缓洪峰的作用,长江中下游地区的水资源丰富程度居全国之最。但是,由于季风和台风等因素的影响,长江中下游地区更容易迎来暴风雨等恶劣天气,暴雨频发会带来更严重的灾害,长江沿岸的洪涝灾害不可能杜绝,却能够进行更好的预防和防范。因此,以长江中下游为研究对象,提高水位流量关系拟合的精度有重要的意义。
枝城素坐落于荆江的源头,与葛洲坝距离很近,向来是鄂西地区的门户、楚蜀交界的咽喉。在枝城境内,长江水系自西向东流经枝城,枝城站位于焦柳铁路线,在长江流域的运输体系中占据重要的位置。枝城水文站属于国家基本水文测站,也是长江中游干流重要的控制站,其地理位置位于葛洲坝的下流。枝城水文站的水文测量工作对三峡水库的泥沙控制起到了很大的作用。枝城水文站的测验河段河床比较稳定,水文验测符合国家相关规范,具有完整、连续的水文数据,数据真实可信。
2.2 数据来源
本文需要使用到的数据为水位流量数据,考虑到拟合效果的精度,本文数据主要来源于枝城水文站,为枝城水文站从2010年1月至2013年9月的每日上午8点监测的水位流量对应数据。
第3章 改进的粒子群算法
3.1 群体智能算法
群体智能算法是一类智能优化算法的统称,研究人员或学者们在观察自然界中生物种群的行为后,研究其种群群体智能的原理,创造出了这一类群体智能算法。由于个体行为的随机性,群体的搜索结果也是具有随机性的,群体中的每个个体集合其自身的经验以及其他成员反馈来的经验,不断调整和改变搜索、寻优的方向,同时,每个个体也会向群体反馈自身经验,供其他个体参考。
群体之间每个个体可以进行交流,通过各自不同的方式进行信息的共享,以相互合作的方式进行搜索。尽管群体中单个个体的搜索行为并不具备智能,但是整个群体中每个个体都是相互有关联的,个体之间存在相互的影响,那么整个群体就表现出一种智能。本文主要采用粒子群优化算法及其改进算法进行研究。
3.2 粒子群算法概述
粒子群算法中,粒子通过自身的最优适应值以及整个粒子群所有粒子的最优适应值来调整自己的搜索行为,直至找到满足既定条件的最优解。粒子群算法源于鸟群觅食行为,鸟群捕食的过程可以进行简化,前提假设是在一块已知的区域内存在着唯一的一块食物,所有鸟对食物的具体位置都是未知的,仅知道自身位置至食物的距离,这个鸟群在这块区域内寻找食物。如果每次整个鸟群都在距离食物最近的鸟的附近区域进行搜索,这无疑是最有效的方法。在每一次搜索之前,鸟群之内都要进行经验的共享,找到距离食物最近的鸟的位置,每只鸟结合自身寻找到的离食物最近的位置,然后去相应的区域范围完成自己的搜索任务,那么通过不断地更新寻找,这个鸟群会无限接近于唯一的食物。
粒子群算法搜索寻优的过程比较简单,算法流程易于理解,。PSO算法起初通过随机初始化的方式初始化每一个粒子的状态。每个粒子自身就代表着实际具体问题的一组可能的解。每个个体粒子都有三种属性特征,即适应值、速度向量和位置向量,这三种属性特征决定着粒子的搜索行为。在整个搜索寻优的过程中,粒子群算法参考鸟群觅食的行为进行模拟,每个个体粒子要向整个粒子群反馈自己的最优适应值,同时也需要获取整个粒子群的最优适应值来决定自己的下一次搜索行为。每个粒子都在既定的解空间内飞行搜索,通过不断迭代搜索,搜索全局最优位置,直至寻找到满足条件的最优全局适应值。
3.3 粒子群算法原理
基本的粒子群算法随机初始化每一个粒子的状态,每一个粒子自身就是问题的一组解向量。在每次迭代中,粒子都要根据获取到的自身的最优适应值和整个粒子群的全局最优适应值,根据这两个适应值,每个粒子要按照式3.5和式3.6是来更新自己的速度和位置,同时通过比较,按照式3.7来更新每个粒子的最优适应值和整个粒子群的全局最优适应值。
粒子群算法中也包含着“进化”的思想,主要反映在迭代更新的过程中。在每一次的迭代过程中,每个粒子都要结合自身的搜索经验和整个粒子群群体的搜素经验来更新自己的搜索状态,根据粒子群中每个个体粒子的适应值的大小、历史位置、历史速度来更新自己的速度和位置。并且,每一次的迭代更新都是不同的,其中具有很强的随机性。
3.3.1 基本粒子群算法的数学描述
假设问题的解空间是维的,在这块解空间中存在一个由个粒子组成的粒子种群。
种群中第个粒子位置、速度可以分别表示为:
种群中第个粒子经历过的最佳位置可以表示为:
粒子群中所有粒子经历过的最佳位置可以表示为:
粒子在迭代寻优的过程中,每个粒子的飞行状态受自身经验和粒子群群体经验的影响,迭代至第代,第个粒子的第d维位置更新过程如下所示:
其中,是粒子在第次迭代中第d维的速度;是粒子在第次迭代中第维的当前位置;是粒子在第维经历过的最佳位置;是整个粒子群在第维中所有粒子经历过的最佳位置;和为加速常数,调节粒子的搜索范围。如果太小,粒子可能会因陷入某一块区域,而错失目标区域,如果太大,粒子可能会飞离目标区域。通常令比较合适。和是0与1之间的随机数,这也是粒子群算法搜索过程具有很强随机性的原因。最大搜索范围Xmax可以防止粒子超出目标搜索区域,设定最大搜索速度Vmax可以防止粒子搜索速度太快而措施目标区域。
在每一次迭代开始之前,要根据适应值,更新和的值,和的更新过程如下:




