英语原文共 12 页，剩余内容已隐藏，支付完成后下载完整资料

毕业论文

英文翻译

原文标题 predicting seed admixture in maize combining flowering characteristics and a lagrangian stochastic dispersion model

译文标题 结合开花特性和拉格朗日随机分散模型预测玉米种子外加剂

结合开花特性和拉格朗日随机分散模型预测玉米种子外加剂

Dominique Dietiker, Peter Stamplowast;, Werner Eugster

Institute of Plant, Animal and Agroecosystem Sciences, ETH Zurich, Universitauml;tsstrasse 2, CH-8092 Zurich, Switzerland

摘要：种子纯度问题在玉米共存研究中受到了很少的关注，而在模拟花粉流动和玉米田间异交的预测工具中却没有考虑到这一问题。为了填补这一空白，我们发展了种子混合模型(Sameth)，该模型能够结合开花特性(花粉沉降、吸附)和拉格朗日随机变量来预测种子外加剂的分散度。色散模型该模型在2007年和2008年从20个田中获得的数据集进行了检验，该数据集的种子与纯合蓝粒杂交的1%混合。首先对模型进行了标定，使用来自6个字段的数据，然后用其余14个字段的数据进行验证。此外，还进行了敏感性分析，以检验不同花粉量释放的结果。所测种子外加剂在0.7%~6%范围内，模型能够模拟种子外加剂R2=0.83。灵敏度分析表明，该模型对绝对释放花粉量敏感，但仍能较准确地预测种子外加剂。由于其可靠性，该模型也可以成为一种有用的方法。对于涉及种子混合物的案例研究方案，以及在哪些领域实现过于复杂和耗时的情况。

1前言

自从采用转基因作物以来，社会上对环境和人类健康可能产生的后果感到关切(Beringer，2000年；Halford和Shewry，2000)。玉米(Zea Mays L.)是一种异种风授粉植物，也是地球上最重要的作物之一，是研究转基因作物与非转基因作物共存的理想选择。特别是通过短距离和长距离花粉流产生的农田之间的异交一直是一个主要议题(例如，Bannert和Stamp，2007年；Goggi等人，2007年； Vogler等人，2009年)。令人惊讶的是，种子外交是一种田间杂交，尽管杂交种子生产田中不定花粉的问题一直为人们所熟知，但其行为却几乎被忽视。从很长一段时间以来，人们就知道了(Hutchcroft，1959年；Burris，2001年；爱尔兰等人，2006年；Astini等人，2009年)。这些研究制定了避免异交的最佳做法，但没有调查这些外国种子在作物生产领域的影响。Diateker等人首次建立并分析了含有1%种子混合料的大片农田数据集。他们得出结论：玉米杂交种的异交形成范围应在0.2%至0.5%之间，以避免收获中的杂质超过欧盟对非转基因饲料和食品的标签规定的0.9%的阈值。

科学界还支持决策者开发预测工具(Aylor等人，2003年；Jarosz等人，2004年；Lipius等人，2006年；Arritt等人，2007年；Angevin等人，2004年) ，2008年)。这些模型能够模拟花粉流动，并能从花期特征(花粉沉降和吸附)预测转基因玉米田与非转基因玉米田在复杂景观中的异交，环境变量(风、温度和湿度)和地形形状。最常见的模拟花粉流的方法是实现拉格朗日离散模型，无论是在 2D(Aylor等人，2003年；Jarosz等人，2004年)或3D(Arritt等人，2007年）。然而，就像分析花粉流研究中发生的情况一样，种子混合剂被忽视了。

因此，本研究的目标是开发一种新的模型，作为上述模型的补充预测工具。ETH的新种子混合模型，我们在这里介绍的苏黎世（Sameth）模型结合了两种不同的方法：（一）玉米开花特性（花粉沉降和吸附）已经得到了很好的研究(e.g. Bassettiand Westgate, 1993a; Westgate et al., 2003)在数学上描述(e.g. Fonseca et al., 2003; Lizaso et al., 2003) （二）在田间范围内用一个拉格朗日散射模型模拟花粉流动(Aylor and Flesch, 2001; Arritt et al., 2007).为了验证Sameth，Dietiker等人建立的数据集。

2材料和方法

2.1模型模块

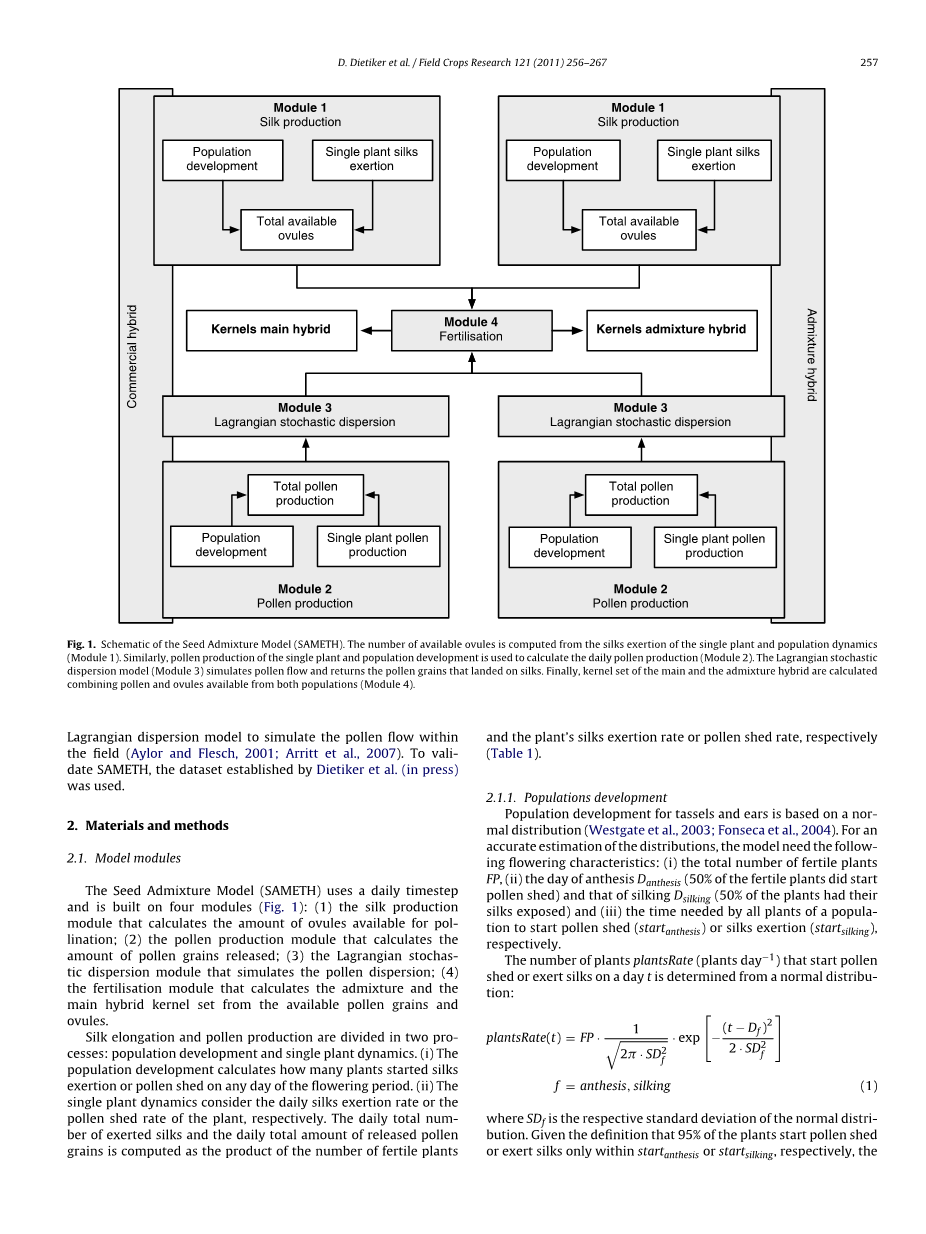
种子混合模型(Sameth)使用一个每日时间步长，并建立在四个模块上(图1)：(1)计算可供授粉的胚珠数量的花粉产生模块；(2)计算花粉释放量的花粉生产模块；(3)模拟花粉散布的拉格朗日随机分散模块；(4) 从可利用的花粉粒和胚珠中计算外加剂和主要杂交核集的受精模块。

花丝伸长和花粉产生分为两个过程：种群生长和单株动态。(1)种群生长计算出有多少植物在开花期的任何一天开始吐丝或脱落花粉。(2)单株动态分别考虑了植株的日放丝率和花粉脱落率。每天施用的丝数和每天释放的花粉颗粒总量被计算为可育植物数量的乘积并且计算出植物的吐丝率或花粉脱落率。

2.1.1种群发展

对于穗粒的种群发展是以正态分布为基础的(Westgate等人，2003年；Fonseca等人，2004年)。为了精确估计分布，该模型需要下列开花特性：(1)可育植株的总数量fp；(2)开花日Danthesis(50%的可育植株开始花粉脱落和吐丝）；(3)一个群体中的所有植物开始花粉脱落(开始萌发)或开始发丝所需的时间(发丝)。

在t天开始花粉脱落或吐丝的植物数量(植物日minus;1)是根据正态分布确定的：

SDF是正态分布的标准差。给出的定义是，95%的植物开始花粉脱落或只在开始发丝或吐丝，这可以简化逼近：

由于startfplusmn;2SDf大致包括正态分布中所有值的95%。这两个值反映了一个群体的遗传均匀性，即小的值表示遗传均匀植物t。开始开花期（花粉脱落或吐丝）接近另一个，因为平均分布不均。

丹尼特和德林的区别被称为花丝间隔(ASI).区分子种群中的ASI(例如，花期和通配线之间的间隔) )和亚群体间的ASI(例如，混合子群体的花期间隔和商业亚群体的育性之间的间隔)。引入了“跨ASI”一词。在本研究中，杂交亚种总是指外加剂亚群体的花期与商品亚种的丝粒之间的间隔。

在t天开始开花的植物数量是通过一天的植物比率的综合来确定的：

t是一年中的一天，t0是种群开始花粉脱落或吐丝的日子，t是t0以后的花期的日子。

2.1.2.花粉吸附与计时

用单分子方程(Lizaso等人，2003年)对植物自身的吐丝过程进行了模拟，结果表明：

如果吐丝是在t天使用的花丝数量(吐丝植物minus;1)，则花丝是穗暴露出的最大吐丝数，r是吐丝消耗率(minus;1天)，t是一年中的一天，ts是t 施放第一批丝的天数，s(D)为吐丝施力期的持续时间，约为吐丝时间的95%左右。在这段时间之外，没有吐丝消耗，比率等于0。另外，还可以考虑通过对丝(T)与丝(T)的除法来考虑相对的吐丝消耗。

可供授粉的胚珠(每一丝对应于一个胚珠)的总日均数，是根据出力丝的植株比数来计算的。

2.1.3.花粉产生与时间

玉米植株的花粉脱落率通常服从正态分布(Lizaso等人，2003年)，可表示为：

式中，shedRate是花粉棚的日速率（谷物植物minus;1天minus;1），t是一年中的一天，tp是植物花粉棚的第一天，PG是植物的总花粉产量（谷物）。 植物minus;1)，p是花粉棚的持续时间(天数)，d决定花粉脱落的强度(天数)。低的d值是植物释放花粉的特征，它们主要在测验中释放花粉。虽然最大花粉量仍然存在，但较高的d值增加了开花初期和开花期结束时的花粉流失量，而在花期中部则减少了花粉流失量。统计上，p/2是正态分布的平均值，d是正态分布的标准差；这可以近似于

每天可供受精的花粉粒数是通过一天的脱落率积分来确定的：

当花粉是在t天可获得的花粉粒数(minus;1)时，t0是群体花粉棚的第一天，t是群体花粉棚开始后的第一天，t是种群花粉棚开始后的第一天。 由拉格朗日随机离散模型计算的被风吹散后附着在丝上的花粉粒的相对数量。

可用于授粉的花粉总数，即谷粒，是在某一天开始花粉脱落的植物数量的乘积。 Tity由这些植物(花粉，Eq)释放。(8)从数学上讲，这个过程可以用求和来表示：

其中t0是群体花粉脱落的第一天，t是t0以后花期的天数。

2.1.4.拉格朗日随机分散模型

拉格朗日随机离散模型(LS)返回花粉颗粒的相对数量，通过模拟杜的三维花粉轨迹，花粉颗粒附着在穗粒上。 液体(大气)该模块的大部分来源于先前公布的LS色散模型(Wilson，2000年；Aylor和Flesch，2001年；Aylor等人，2003年；Arritt等人，2007年)， 然而，为了更好地模拟田间花粉的扩散，特别是冠层内的风场修正和行透性，进行了调整和添加。

流速分量u随时间变化的描述可以用雷诺分解表示为平均u和湍流u之和，术语：

Legg和Raupach(1982)证明了像随机游动模型一样的马尔可夫链过程可以用布朗运动的广义Langevin方程来描述。他们还强调没有马尔可夫 过程可以精确地描述湍流中的流体颗粒速度，但如果时间步长t比拉格朗日时间sca小得多，则马尔可夫过程等价于Langevin方程。 对该工艺进行了研究。Langevin方程的一般公式是：

其中dε是具有零均值和方差dt的高斯白噪声项，a和b是决定模型的Langevin系数(Wilson和Sawford，1996)。实际上，a描述的是自相关器。 湍流的一部分和随机的部分；根据系数，可以产生几种算法。

在该算法中，由拉格朗日湍流速度u、拉格朗日自相关函数RL和随机项u，(Smith，1968)预测拉格朗日湍流速度u：

假设速度波动u在短周期t上是平稳的，随机高斯扰动u可以用其标准差来表示，即：

其中，i是速度波动u的标准差，在一个三维(i=1，2，3)中，是一个高斯随机项，均值为零，方差为1。可以注意到 较大的i(即强湍流)放大了u，i，从而增大了可能的拉格朗日湍流速度的范围。在林冠内，标准偏差i与林分成正比。 林冠顶部ARD偏差I；

其中z是树冠的高度，HC是树冠的高度。在冠层上方(zgt;hc)，标准差i等于参考值i。

拉格朗日自相关函数RL与粒子拉格朗日时间尺度TP呈指数关系(Arya，1999)：

对于很大的时间步长(TTP)，RL接近于0，因此湍流速度仅取决于湍流速度，因此是完全随机的，与其以前的数值无关。水平维(i=1，2)中的粒子拉格朗日时间尺度等于流体拉格朗日时间尺度TL，定义为：

然而，在垂直维上，流体拉格朗日时间尺度由于重力的存在而得到修正，因而具有更快的去相关性。跟随Sawford和Guest(1991)拉格朗日时间 垂直维度中的比例变成：

其中ˇ是一个无量纲系数，其值为1.5(Sawford and Guest，1991年)，S是玉米花粉的沉降速度(0.25cm sminus;2，Aylor等，2003年)。标准差3为。

新粒子的位置由其当前位置x(T)和速度u(T)确定。在垂直方向上，考虑了重力的影响。

其中delta;z是克罗内克函数。

从三维位置x(T)到x(T)，在林冠内移动的粒子可以击中冠层元素或土壤表面。模型分析了粒子的线性轨迹， 如果一个实体元素被击中，它将返回此目标物的位置。

树冠元素的结构尽可能简单。植物行(75厘米距离)表示为连续的垂直二维膜，其对粒子的渗透性取决于hei。 它与LAI成反比，假设花粉在密集的LAI时不能通过一行。这是对现实的简单表达，但很容易实现， T节省了计算时间，LAI剖面的描述在科学文献中得到了广泛的报道。因此，从Maddonni等人测量的叶面积剖面中获得了通透性。 (2001年)在玉米檐下的情况如下：

通透性返回花粉粒在z高度横越一行的概率(从0到1)。在穗丝高度(z=hs)定义的通透性为0，这意味着所有的花粉粒都是相同的。如果他们在相应的高度横过一排植物，就会被吸附弄得干干净净。相反，所有的粒子都可以在顶上和树冠底部通过这一行(=1)。渗透率函数集中在穗丝的高度通过hs/hc比。

LS色散模块每天以时间步长t=0.5s计算已知粒子数k=10，000的路径(用灵

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[20635]，资料为PDF文档或Word文档，PDF文档可免费转换为Word