英语原文共 6 页，剩余内容已隐藏，支付完成后下载完整资料

河流径流与降水的多重分形:形态分析与小波方法的比较

Multifractality of river runoff and precipitation: comparison of fluctuation analysis and wavelet methods[J]. Jan W. Kantelhardt,Diego Rybski,Stephan A. Zschiegner,Peter Braun,Eva Koscielny-Bunde,Valerie Livina,Shlomo Havlin,Armin Bunde. Physica A: Statistical Mechanics and its Applications. 2003(1)

摘要

研究了河流流量和降水记录的多重分形时间尺度特征。我们将多重分形去趋势波动分析方法的结果与小波变换模极大值技术的结果进行了比较，得到了误差范围内的一致性。与以往的研究相比，我们发现径流的非普遍行为:在长时间尺度上，在几周的交叉时间尺度以上，径流记录是由不同河流在大范围内的波动指数来描述的。在降水记录中也观察到类似的变化，这些记录表现出较弱但仍然显著的多重分形特征。对于所有径流记录，多重分形的类型与二项多重分形模型的修正版本一致，而一些降水记录似乎需要不同的模型。

关键字

时间序列；长期的相关性；分；波动分析；小波分析；径流；降水

河流流量分析有着悠久的历史。半个多世纪前，工程师赫斯特就发现，不同河流的径流记录显示出“长期的统计相关性”[1]。后来，许多其他地球物理记录也报道了这种长期相关波动行为，包括降水数据[2]、[3]，参见参考文献[4]。

这些原始方法只关注波动完全分布的绝对值或方差，分别可视为第一时刻F1(s)[1]、[2]、[3]和第二时刻F2(s)[5]。在过去的十年中，人们已经认识到，要对径流记录[6]、[7]进行完整的描述，需要多重分形描述。因此，我们必须考虑所有时刻Fq(s)来充分描述记录。这些记录的多重分形描述可以被视为每个站点或河流的“指纹”，这些“指纹”可以作为最先进的降雨径流模型的一个有效的非平凡的试验台。

由于多重分形分析不是一项容易的工作，特别是当数据受到趋势或其他非平稳性的影响时，例如由于建筑工程对河床进行了修改或由于气候变化，因此比较不同方法的结果是有用的。我们利用多重分形去趋势波动分析(MF-DFA)方法[8](也见[9]，[10])和已有的小波变换模极大值(WTMM)技术[11]，[12]研究了多重分形，发现两种方法的结果是等价的。这两种方法都不同于Lovejoy和Schertzer[6]，[7]引入水文学的多重分形方法。

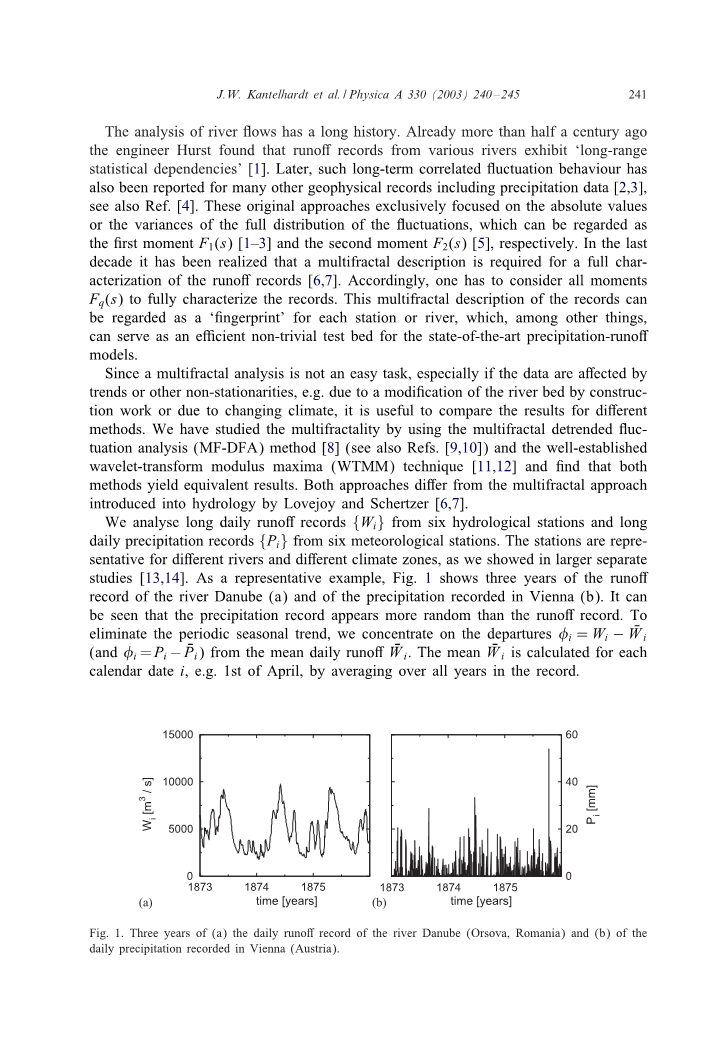
我们分析了6个水文站点的长日径流记录和6个气象站点的长日降水记录。这些监测站代表着不同的河流和不同的气候区域，正如我们在[13][14]的大型独立研究中所展示的那样。作为一个典型的例子，图1显示了多瑙河(a)三年的径流记录和维也纳(b)三年的降水量记录。可以看出，降水记录比径流记录更具有随机性。为了消除周期性的季节性趋势，我们集中研究了平均日径流的离差(和)。平均数是指每个日历日，例如4月1日，在有记录的所有年份中取平均数。

MF-DFA过程[8],时刻Fq(s)(i)计算了整合系列,系列(2)分裂成段的长度,(3)计算均方偏差F2(nu;,s)多项式适合在每个段nu;,(iv)平均(F2(nu;,s)]q / 2 /所有的片段,和(v)的qth根。本文在step (iii) (MF-DFA3)的拟合过程中使用了三阶多项式，消除了数据的二次趋势。我们认为,积极的和消极的时刻Fq (s)(问范围从minus;10 10),并确定他们的时间尺度之间的年代= 8和N / 5,其中N是该系列的长度。图2为两个代表性水文站点的MF-DFA3(填充符号)结果。在大的时间尺度上，在交叉发生的10-100天以上，我们观察到幂律尺度行为，其中比例指数h(q)(图2中的斜率)依赖于q的值，这种行为代表了多重分形的存在。

为了测试MF-DFA方法，我们采用了成熟的WTMM技术，该技术也是去趋势的，但基于小波分析而不是多项式拟合过程。对于该方法的完整描述，我们参考[11][12]。首先,小波变换的离职phi;i计算。小波的g (x)我们选择高斯函数的三阶导数,g (x) = d3 (eminus;x2/2) / dx3正交二次趋势。现在,对于一个给定的规模s′,一个确定的局部极大值的位置倪T (n, s′) | |,所以| T (niminus;1, s′) | lt; | T (ni, s′) |⩾| T (ni 1, s′) |。然后，对所有最大值ni取|T(ni,s )|q的平均，得到WTMM划分和Z(q,s )。为了保持Z(q,s )对s 单调[12]的依赖关系，WTMM方法必须使用一个额外的上限值过程。预期的扩展行为是Z(q、s′)sim;(s′)tau;(q),在tau;Renyi指数(q)。因为tau;(q)相关指数h(q)h(q)=(tau;(q) 1]/ q[8]。

我们将s =s/8与MF-DFA的结果进行比较，因为我们使用的小波可以很好地逼近在一个大小为8s 的窗口内(即在两侧4个标准差范围内)，这个窗口大小对应的是MF-DFA中的段长s。从图2中可以看出，对于我们考虑的q值，两种方法的结果是等效的。

利用MF-DFA结果，我们从式(1)中确定了6条径流记录的h(q)和6条降水记录的若干q值。由于Fq(s)交叉发生在10-100天的时间尺度上，我们只考虑了足够长的时间尺度(1年以上)，其中的结果可以很好地伸缩。径流数据h(q)如图3所示，降水数据h(q)如图4所示。结合计算结果，给出了最小二乘拟合公式

1. 它对应于一个广义二项式多重分形模型[13]，并且可以得到，也见[4]，[8]。

图中还报告了两个参数a和b的值。仅用这两个参数对所有河流的结果拟合得出奇的好(如图3所示)，我们也可以选择Hurst指数h(1)和persistence指数h(2)来代替a和b。从对两个时刻的认识出发，所有其他的时刻也随之而来。

这一令人惊讶的结果不适用于降水记录。从图4(c)和(f)中可以看出，存在Eq.(3)不能很好地描述多重分形尺度行为的站点。Rybski等人认为Eq.(3)仅适用于50%左右的降水记录[14]。

在广义二项式多重分形模型中，多重分形的强度由h(q)的渐近值的差来描述。我们注意到,这个参数是相同的奇异谱的宽度(alpha;)f = 0。研究41河径流记录[13],我们得到一个平均Delta;alpha;= 0.49plusmn;0.16,这表明,而强大的分形在长时间尺度。而降水记录的多重分形特征较弱。的平均Delta;alpha;= 0.29plusmn;0.14 83条记录[14]。

我们的研究结果为h(q)可能与不同的拟设h(q)= 1 h′minus;C1(qalpha;′minus;1minus;1)/(alpha;′minus;1)三个参数h′,C1,和alpha;′(LS拟设),已经被洛夫乔伊,Schertzer,和同事[6],[7]成功地描述降雨和径流的多重分形行为记录问qgt; 0。这两种方法之间的定量比较受到了抑制，因为在这里我们只考虑了较长的时间尺度并使用了去趋势方法。我们想指出，公式(3)对于h(q)不仅适用于正q值，而且适用于负q值。值得注意的是，径流记录只需要两个参数就可以拟合数据。对于降水数据，需要像LS ansatz那样的三个参数或者不同的方案。

综上所述，我们使用MF-DFA和WTMM方法分析了长河流量记录和长降水记录。我们在误差范围内得到了一致的结果，发现径流记录具有比降水记录更强的多重分形特征。令人惊讶的是，所有径流记录中出现的多重分形类型与二项多重分形模型的修正版本一致，该模型支持洛夫乔伊和谢尔策提出的河流径流“普遍”多重分形行为的观点。相反，根据Ref.[14]，一些降水记录似乎需要不同的描述，或者像LS ansatz那样使用三个参数进行匹配。多重分形指数可以看作是每个站点的“指纹”。此外，基于改进的二项式多重分形模型的多重分形发生器可用于为每个径流记录和一些降水记录生成具有特定属性的替代数据。

我们要感谢德国科学基金会(DFG)、德国联邦教育和研究部(BMBF)、以色列科学基金会(ISF)和Minerva基金会的财政支持。我们还要感谢波茨坦皮克的H. Osterle提供了一些观测数据。

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[19496]，资料为PDF文档或Word文档，PDF文档可免费转换为Word