摘 要

本文基于有限元软件MSC.Patran/Nastran研究复合材料圆柱壳的自由振动特性，基于LMC Virtual.Lab软件的边界元法研究声辐射特性，其结果对于圆柱壳结构的减振降噪具有一定指导意义。

本文主要研究了复合材料圆柱壳的边界条件、铺层角度、铺层层数、厚径比、长径比和弹性模量比对固有频率的影响，研究了铺层角度、厚径比对声辐射的影响，并对比研究了与普通钢材圆柱壳的声振差异。振动结果表明，在高模态时：[0°/90°/0°]对应的频率最高；等厚加层对频率影响不大；厚径比增大会显著提高固有频率；长径比增大会显著降低固有频率；弹性模量比会明显提高固有频率。而在低模态时：[0°/30°/0°]对应的频率最高，其他参数影响不太大。声辐射结果表明：声功率级和声辐射效率均为[0°/0°/0°/0°]最大，[45°/0°/45°/0°]最小，厚径比0.03最小，厚径比0.01最小。

关键词：复合材料；圆柱壳；振动；声辐射

Abstract

Based on the finite element software MSC. Patran/Nastran, free vibration characteristics of composite cylindrical shell is studied in this paper. And based on the boundary element method software LMC. Virtual.Lab, acoustic radiation characteristics is also studied in the paper. The result has certain guiding significance of cylindrical shell structure vibration and noise reduction.

This paper mainly studies the effects of boundary conditions, layer number and thickness to diameter ratio, length to diameter ratio and elastic modulus ratio of composite cylindrical shell on the natural frequencies, the effects of the Angle of the layer, thick diameter ratio on the sound radiation, and differences compared with steel cylindrical shell. Results show that the vibration in the anti-embrittlement states: [0°/90°/0°] corresponding to the highest frequency; Isopachic lamination has little effect on frequency. The natural frequency is significantly increased by the increase of the thickness ratio. The natural frequency can be significantly reduced by increasing the diameter ratio. The elastic modulus ratio obviously increases the natural frequency. While in low modal: [0°/30°/0°] corresponding to the highest frequency, the influence of other parameters is too big. Acoustic radiation results show that the sound power level and sound radiation efficiency is all that [0°/0°/0°/0°] maximum, [45°/0°/45°/0°] minimum, thickness to diameter ratio of 0.03 maximum, thickness to diameter ratio of 0.01 minimum.

Key Words：composite；cylindrical shell；vibration；sound radiation

目 录

第1章 绪论 1

1.1 研究对象及意义 1

1.1.1 复合材料概述 1

1.1.2 复合材料壳体 1

1.2 研究理论及现状 2

1.2.1 复合材料结构理论 2

1.2.2 振动研究理论及现状 2

1.2.3 声学研究理论及现状 3

1.3 研究内容 4

第2章 复合材料圆柱壳理论 5

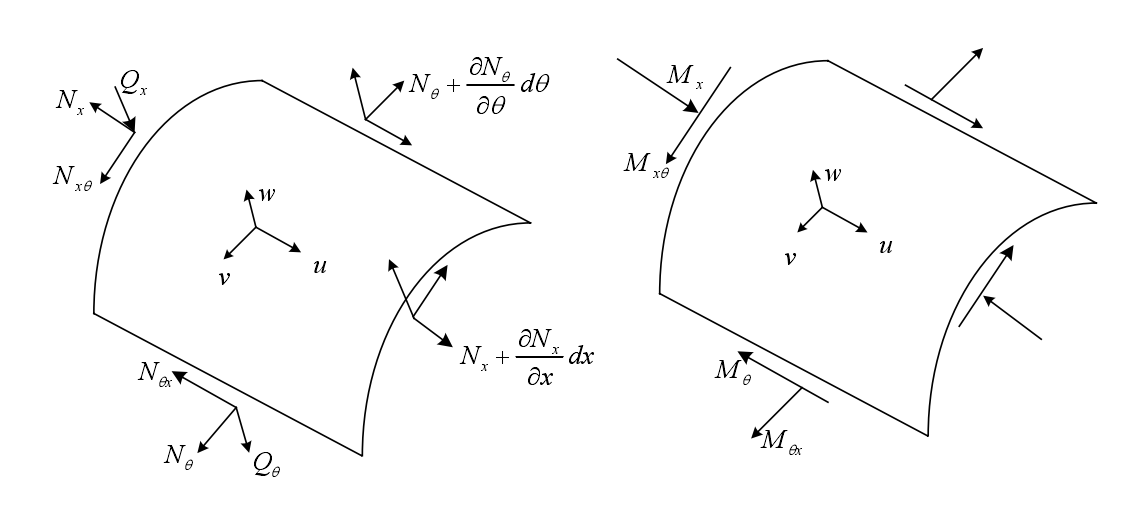
2.1 复合材料圆柱壳振动理论 5

2.1.1 一阶剪切壳体理论 5

2.1.2 三维弹性壳体理论 6

2.1.3 有限元法 7

2.1.4 振动方程 8

2.2 复合材料圆柱壳声学理论 10

2.2.1 声波方程、Helmholtz方程 10

2.2.2 边界积分方程及其数值离散 11

第3章 复合材料圆柱壳振动特性计算 13

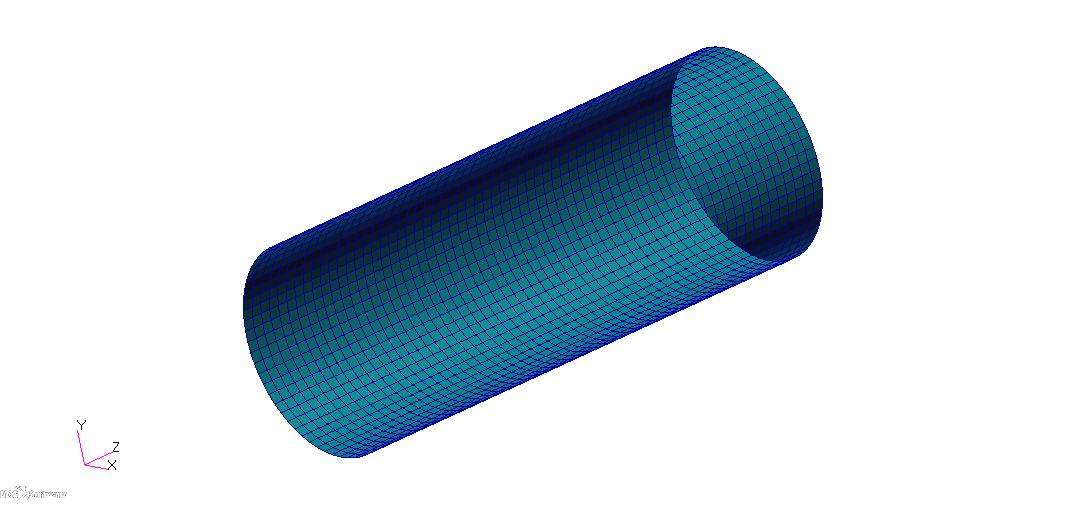
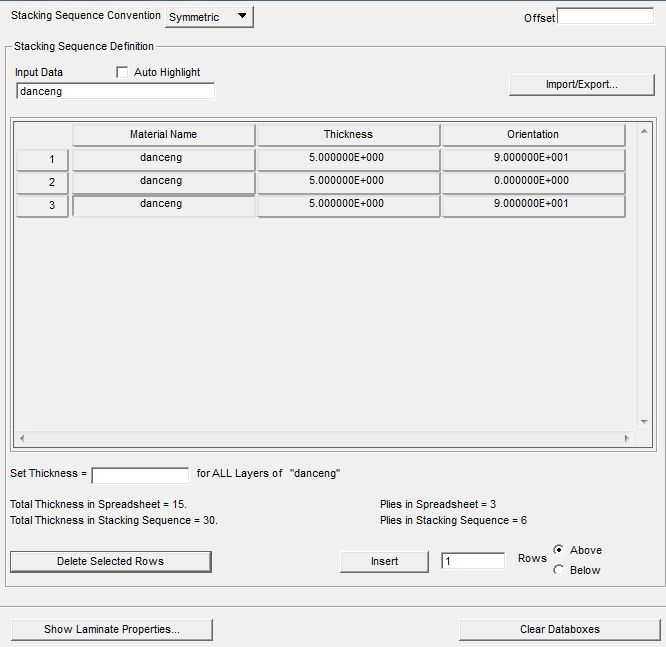
3.1有限元模型 13

3.2网格无关性研究 15

3.3边界条件对固有频率影响 16

3.4铺层角度对固有频率影响 18

3.5铺层层数对固有频率影响 20

3.6厚径比对固有频率影响 22

3.7长径比对固有频率影响 24

3.8弹性模量比对固有频率影响 25

3.9对比研究 27

第4章 复合材料圆柱壳声辐射特性计算 31

4.1建模过程 31

4.2铺层角度对声辐射影响 32

4.3厚径比对声辐射影响 34

4.4对比研究 34

第5章 结论 37

5.1 振动分析 37

5.2 减振设计 37

参考文献 38

致 谢 40

第1章 绪论

本章结合复合材料结构的发展背景和重要意义，介绍了复合材料的成分组成、力学特性等基本内容，将工程结构中的一种典型结构——圆柱壳定为本文研究对象，总结了研究理论及现状，并依据船舶与海洋工程领域对结构振动与声学要求，确定了本文分析和仿真方法，以及复合材料圆柱壳振动与声辐射特性的内容。

1.1 研究对象及意义

1.1.1 复合材料概述

复合材料是富有研究及应用潜力的战略性材料，几十年来发展迅猛，在制造水平、材料性能等方面都有着大幅提升。采用复合材料来制造船舶舰艇及其结构部件，如潜艇、导流罩、管路系统等，已经是工程领域的一大趋势，有着广泛的实践应用和深入的理论研究。

复合材料，从广义上讲，是指经人工复合而成的一种新型材料，其系统复杂，由两种及以上不同性能形态的材料组成，采用物理或化学方法加工，表现出不同于其组分材料的特性。复合材料的优势在于弥补了组分材料的部分缺点，并且新生出一些优良性能。

复合材料中的结构性复合材料在技术发展、经济效率和社会应用等方面都占有压倒性的优势，通常情况下，复合材料包括基体材料（聚合物、金属、无机非金属等）和增强材料（颗粒增强、纤维增强、片材增强等）。基体材料的作用包括支撑增强材料、传递载荷、保持形状等；增强材料的作用主要是承担载荷。

1.1.2 复合材料壳体

在众多复合材料的结构中，由纤维增强等复合材料（增强材料主要有玻璃纤维、碳纤维等，基体材料主要有树脂基体、金属基体、陶瓷基体等）制成的结构性能优良，不仅比强度高、比模量大、工艺优良、设计性好，还耐腐蚀、抗疲劳，等等。

在梁、板、壳等基本结构中，复合材料壳体的优势相当突出，若作为承载结构，复合材料壳体的弯矩、扭矩很小，主要承受拉压和剪切应力，能够以较小的厚度来承受相当大的载荷，且覆盖面积大，减轻了结构重量。相比于敷设阻尼层，复合材料不额外增加壳体重量，不存在脱落问题，稳定性高。因此本文选择复合材料圆柱壳作为研究对象。

复合材料不同于常规材料，其复合效应、层次效应、界面效应、各向异性等复杂特性，导致由均匀材料为基础的很多力学理论和分析方法已无法准确反映、概括和应用到复合材料中。复合材料壳体的出现，一方面，促进了材料科学和工程学的发展，另一方面，使得有关振动与声学理论研究的复杂化，仿真中的建模、计算等过程也变得困难，因此具有研究的必要和意义。

1.2 研究理论及现状

1.2.1 复合材料结构理论

有关复合材料壳体的理论研究，目前包括等效单层理论（包括层合薄壳理论，一阶剪切变形壳体理论和高阶剪切变形理论）、分层理论、锯齿理论和三维弹性理论等，简述如下：

1、以Love、Reissner、Donnell、Vlasov^[1]等各向同性材料薄壳理论发展而来的层合薄壳理论采用Kirchhoff-Love直法线假设，近似假设z/R远小于1（其中z为厚度坐标，R为曲率半径），并由此进行简化，得到含较少未知变量的简单的表达式。但因没有考虑横截面剪切等因素，一般仅适用于低阶振动。

2、一阶剪切理论和高阶剪切理论考虑了壳体横截面的剪切效应，结果更为精确。前者假设横向剪切应变沿壳体厚度方向为常数，理论修正后引入了剪切修正因子，如Reddy^[2]和Qatu^[3]等。后者根据不同研究理论，引入不同未知变量，以不同阶数展开，满足了壳体表面剪切应力为零的条件，如Reddy和Liu^[4]的三阶剪切壳体理论，Viloa等^[5]的含9个未知位移变量的理论。

3、分层理论对所有的铺层都引入独立的位移场函数，更加准确地描述了力学特征，但因依赖层数的未知量数量的增加，导致计算量明显增加。

4、锯齿理论包括一阶理论和高阶理论，在位移展开式中添加锯齿函数，满足层间应力连续条件。如Carrera^[6]采用多项式展开了中面和法面的位移，并添加了锯齿函数。

1.2.2 振动研究理论及现状

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：