英语原文共 9 页

第四章 仿真能力验证

我进行了七项验证研究，以测试新功能的准确性：三项用于流体动力学模块（第4.1节），两项用于系泊系统模块（第4.2节），两项用于整个系统（第4.3节）。最后一组验证练习将我的时域模拟工具的结果与频域模型的结果进行了比较。正如我在本章中所讨论的，所有的验证练习都得到了有利的结果。这使我有信心在第5章和第6章中对海上浮式风力发电机的动态特性进行更深入的研究。

此外，虽然在此处没有明确记录，但是新增加的支撑平台自由度(DOF)在FAST中产生的动力学结果与ADAMS非常契合。我在第6章提供了一些这类例子。

我对所有这些验证练习进行了建模比较。一旦实验数据可用，将在稍后验证完全耦合的模拟工具。

4.1流体动力学模块的验证

我进行了三次验证测试来检查HydroDyn的流体动力学模块。首先，在第4.1.1节中，我验证了由HydroDyn计算出的波高时间序列的PSD与HydroDyn的波谱输入参数规定的目标JONSWAP谱相匹配。其次，我验证了作为HydroDyn输入的WAMIT的输出与不同的辐射/衍射解算器产生的输出相似（见第4.1.2节）。第三，我验证了在我的流体动力学模块中计算的辐射脉冲响应函数与使用WAMIT的独立时频转换工具计算的相同[58]。我将这些结果放了在第4.1.3节。

4.1.1波高与目标波谱

不规则海况（随机波）在HydroDyn中的建模是通过方程（2-9）的逆傅立叶变换实现的，它代表了大量周期波和平面波分量的叠加。这些波分量的振幅平均由规定的波谱决定。之所以说平均，是因为通过高斯白噪声(WGN)过程实现了随机性。该过程不仅考虑均匀分布的随机相位，还考虑正态分布的振幅（见第2.4.1.1节）。在Hydrodyn中，方程（2-9）是使用计算效率高的快速傅立叶变换(FFT)实现的[92]。

我运行了一个简易的测试来检查我是否在HydroDyn中准确地实现了这些数学关系。我计算了四个波高时间序列，每个时间序列都由有效波高H_s为5.49 m、谱峰周期T_p为14.656s或谱峰频率约0.429 rad/s的Pierson-Moskowitz波谱确定[见方程（2-20）]。这个波谱相当于JONSWAP波谱，其峰形参数的默认值（单位）由方程（2-19）给出。每个波高时间序列的时长为10000秒（即，每一个都不到3小时），通过选择非相似的随机数种子来区分。

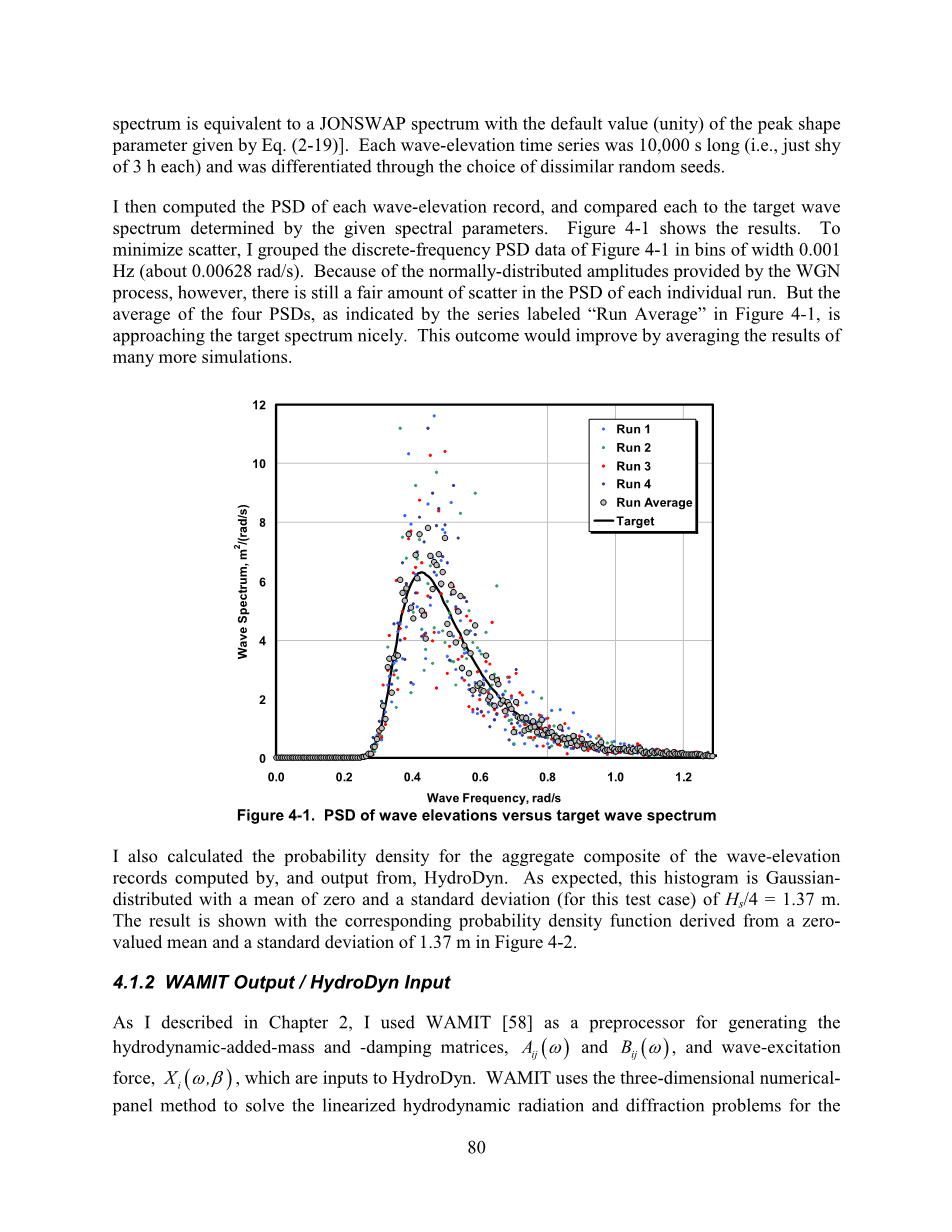
之后我计算了每个波高记录的PSD值，并将其与由给定的波谱参数所确定的目标波谱进行了比较。结果如图4-1所示。为了使散射最小化，我将图4-1中的离散频率PSD数据分组到0.001 Hz（约0.00628 rad/s）的箱中。然而，由于高斯白噪声(WGN)过程提供的正态分布振幅，在每个运行的PSD中仍然存在相当数量的散射。但是，如图4-1中记为“运行结果平均值”的系列所示，四组PSD的平均值与目标波谱结合地很好。通过进行更多次的模拟并对结果取平均值，这一结论还将继续改善。

我还计算了由HydroDyn计算和输出的波高记录的复合聚集体的概率密度。正如预期，该直方图呈平均值为零的高斯分布，标准差（对于本测试案例）为H_s/4=1.37 m。结果显示为图4-2中以均值为零和标准差为1.37 m导出的相应概率密度函数。

4.1.2 WAMIT输出/HydroDyn输入

正如我在第2章中所描述的，我使用WAMIT[58]为预处理器生成了水动力附加质量和阻尼矩阵A_ij(omega;)和B_ij(omega;)以及波浪激励力X_i(omega;,beta;)，并将它们输入HydroDyn。WAMIT使用三维数值面元法来求解海洋平台与面波在频域上相互作用的线性水动力辐射和衍射问题。WAMIT忽略了海流或航速对辐射和衍射问题的影响以及高阶效应的影响。

12

Run 1

Run 2

Run 3

Run 4

Run Average Target

10

8

Wave Sum, m2/(rad/s)

6

4

2

0

0.0 0.2 0.4 0.6 0.8 1.0 1.2

波频率 , rad/s

图 4-1. 波高与目标波谱的PSD

0.4

HydroDyn Output Gaussian Distribution

0.3

Probability Density, 1/m

0.2

0.1

0.0

-6 -4 -2 0 2 4 6

波高, m

图4-2. 波高概率密度

因为我的模拟工具生成的水动力解和水动力输入相当，这也验证了WAMIT的结果可接受性良好。因此，我运行了一个测试，以确保生成的WAMIT输出与通过不同的辐射/衍射解算器计算的输出相似。

在WAMIT中，我用两个对称的几何平面模拟了一个在四分之一的船身内有2400个矩形板的驳船。与线性理论相一致，我只需要将船体的水下部分建立网格。图4-3显示了两个对称的面板网格。为了避免在WAMIT分析中振荡水柱(OWC)的影响，我在月池自由表面下0.01 m处覆盖了一块的固定板。在一次使用NAME模拟振荡水柱(OWC)的尝试中，结果认为该板可以相对于驳船自由移动。图4-4显示了用于NAME分析的面板网格。

图4-3. WAMIT中ITI能源驳船的面板网

图4-4.NAME中使用的ITI能源驳船的面板网格

为了提高WAMIT结果的准确性，我选择改写三个默认设置：（1）对数奇异性集合分析，（2）使用直接算法求解线性方程组，（3）通过将船身面板自动投影到自由表面来消除不规则频率的影响。这些设置是必要的，因为一些面板位于靠近自由表面的平面内，驳船具有较大的水平面区域，随后的

分析需要高频结果。在驳船的所有六种刚体运动模式中（在矩阵下标中，1代表纵荡，2代表横荡，3代表垂荡，4代表横摇，5代表纵摇，6代表垂摇）比较了水动力附加质量和阻尼矩阵，对每个频率得出一个6times;6的矩阵。因为NAME中将每个板块视为一个独立个体，所以在每个频率下产生的矩阵大小为12times;12。不过，为了帮助进行比较，NAME通过后处理将这些矩阵少到减了6times;6。此次测试中未考虑水力波浪激励力。

图4-5显示了并列比较的结果。由于水动力附加质量和阻尼矩阵在没有海流或航速的情况下是对称的，因此只用显示上三角矩阵的元素。同样，由于驳船的对称性，与频率相关的附加质量和阻尼矩阵的横荡元素(A₁₁和B₁₁)与纵荡元素(A₂₂和B₂₂)相同。类似地，横摇元素(A₄₄和B₄₄)与纵摇元素(A₅₅和B₅₅)相同。其余未显示的矩阵元素为零值或非常接近零值。

40E 6 8E 6

A11 WAMIT A22 WAMIT A33 WAMIT A11 NAME A22 NAME A33 NAME

B11 WAMIT B22 WAMIT B33 WAMIT B11 NAME B22 NAME B33 NAME

30E 6 6E 6

Force-Translation Modes, kg

Force-Translation Modes, kg/s

20E 6 4E 6

10E 6 2E 6

0E 6

0 1 2 3 4

Frequency, rad/s

0E 6

0 1 2 3 4

Frequency, rad/s

20E 8 8E 8

A44 WAMIT A55 WAMIT A66 WAMIT A44 NAME A55 NAME A66 NAME

B44 WAMIT B55 WAMIT B66 WAMIT B44 NAME B55 NAME B66 NAME

15E 8 6E 8

Moment-Rotation Modes, kg·m2

Moment-Rotation Modes, kg·m2/s

10E 8 4E 8

5E 8 2E 8

0E 8

0 1 2 3 4

Frequency, rad/s

0E 8

0 1 2 3 4

Frequency, rad/s

30E 6 30E 6

A15 WAMIT A24 WAMIT A15 NAME A24 NAME

B15 WAMIT

B24 WAMIT B15 NAME

B24 NAME

20E 6 20E 6

Frc-Rot amp; Mom-Trans Modes, kg·m

Frc-Rot amp; Mom-Trans Modes, kg·m/s

10E 6 10E 6

0E 6 0E 6

-10E 6 -10E 6

-20E 6 -20E 6

-30E 6

0 1 2 3 4

Frequency, rad/s

-30E 6

0 1 2 3 4

Frequency, rad/slt;

资料编号：[3333]