英语原文共 15 页，剩余内容已隐藏，支付完成后下载完整资料

浅谈海上风险评估 Jason R. W. Merrick and Rene van Dorp

最近几年，风险研究被广泛运用于海上交通领域，这些研究对于海上交通有着一定的影响。首先是威廉王子湾的风险评估，它做的很好，但在国家研究理事会看来却还是有缺陷的，它对结果的不确定性是无法评估。评估这种不确定性的困难在于要在这种动态和数据稀缺的应用领域中建立风险模型需要许多不同的技术。在以前的文章中，我们已经提出了海上风险不确定性的两种必要的方法了，一种是利用贝叶斯模拟事故发生的潜在威胁情况，另一种就是利用贝叶斯多元回归分析这些事故的因素和事故专家判断之间的关系。在这篇文章中，我们结合这两种方法对两个个案的风险和不确定性进行全面研究。第一个就旧金山湾建议轮渡服务扩展的影响评估。另一个是美国最大的轮渡系统-----华盛顿州立轮渡的分险评估。

关键词：海上运输；风险分析；不确定性分析

1. 简介

海上运输是美国经济的重要组成部分，也包括墨西哥和加拿大，他们95%的国外贸易和25%的国内贸都依赖于海上运输，每年货物的总价值也高达1万亿美元（国家调查委员会，2000）。然而，事故的例子确是屡见不鲜，埃克森·瓦尔迪兹号的搁浅，自由企业先驱号的倾覆，爱沙尼亚客渡船的事故hellip;hellip;这些都是我们所熟知的海上运输事故，这些事故造成了严重的环境污染和大规模的人员财产损失。单独就是清理费，埃克森·瓦尔迪兹号事故就一已对埃克森公司造成了22亿美元的损失。这就引发了一系列疑问——如何去防止这些事故，再者如何去减少事故造成的损失。

风险管理已成为公司海上运输部门运营决策的重要组成部分，也是一个重要的研究领域。早期的工作在于船舶安全评估或海上结构，比如核动力设备（Pravda ＆ Lightner,1996），液化天然气船，油气平台。在近一段时间，概率风险评估（贝德福德、库克，2001）被引入海上风险评估领域。

威廉王子湾（PWS）风险评估（麦里克等，2000,2002），华盛顿州立轮渡(WSF)风险评估和一个旧金山湾的暴露评估，这是海上风险评估领域的三个成功案例。他们的研究结论被广泛运用于投资决策之中，在美国的海上运输管理中也起着重要作用。

在海上港口系统中，交通形势无时不在变化，这些变化的动态性，事实上，还有其他情况变量，如风、能见度、冰况，会导致风险等级随时变化。这就需要利用模拟来精确建模交通方式的变化所带来的影响，可以通过介绍新的交通规则、增加或减少特定港口的交通量来减少风险。此外，特定港口的事故数据较少，这就需要利用专家判断来估计事故概率。

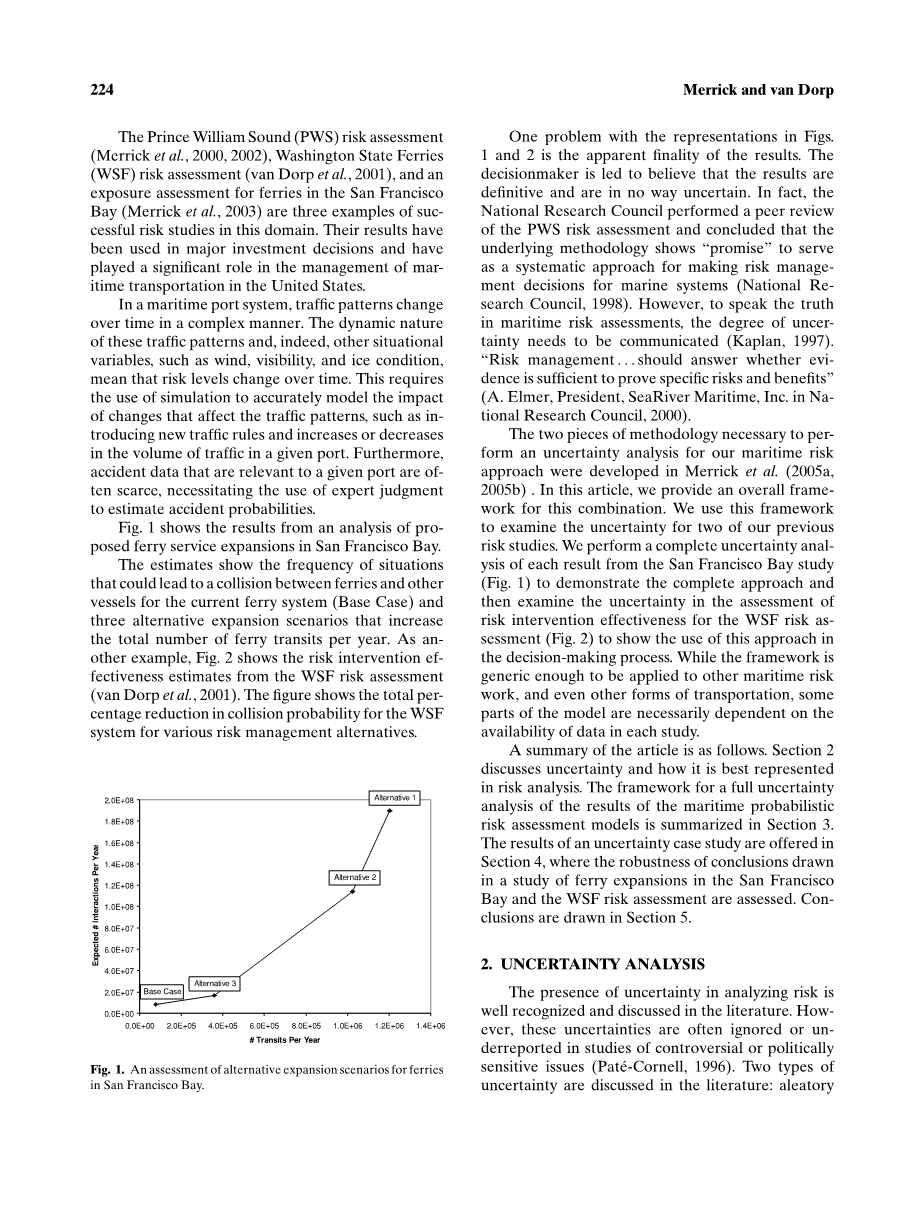
表一给出了旧金山湾渡轮服务扩展的分析结果。

据估计，自目前的轮渡系统中看，这些新的交通变量的出现可能会导致渡轮和其他船舶碰撞，提出三种可供选择的方案中，从中选择，从而避免每年渡轮游客的总人数提高的风险。另一个例子，表2我们可以从华盛顿渡轮风险分析中看出风险干预的有效性。从图表中看出，在运用多种风险管理方案下，碰撞率的总体百分率已经下降。

表中表示也有一个问题。1和2所提出的是个终结的结论，决策者被引导去相信这个结论是肯定而正确的。可事实上，国家研究理事会对威廉王子湾风险评估进行了回顾，并总结出其风险评估的基本方法就是“承诺”服务，这就理所当然地成为了海事系统制定风险管理决策的系统方法（国家研究理事会，1998）。然而，论及海上风险评估的真理，其不确定度仍需考虑。“风险管理hellip;hellip;应该回答是否有证据足以证明特定的风险和收益”（A·埃尔默，总裁，海河海事公司，国家探究理事会，2000）

麦里克等人提出要对海上风险方案的不确定性分析需要执行两种方案。在这篇文章中，我们为他们列出了个总体框架。我们使用这个框架来检验我们以前的不确定度风险研究，我们对旧金山湾的每一个结果进行完整分析，从而展示这种不确定性分析的方法。然后检验不确定性的评估对于WSF风险评估的风险干预的有效性从而显示该方法在决策过程中的使用。这个框架是可以通用于其他海上风险工作，甚至其他形式的运输，不过这个模型的一些部分很依赖于数据的可用性。

文章的概要如下，第二节讨论不确定性和如何它是风险分析的最好代表。第三节就是总结了这个不确定性分析的完整框架。第四节将会提供一个事件的不确定性分析结果，最后在第五节进行总结。

1. 不确定性分析

在风险分析中存在不确定性早已在文献中被公认与讨论了。然而这些不确定性因素经常在研究中被忽视或低估(Patacute; e-Cornell, 1996).有两种形式的不确定性经常在文献中被讨论：偶然的不确定性（系统本身的随机性）和认知的不确定性（对系统知识的匮乏）。在模型的意义上，偶然不确定性表现为一个概率模型对风险分析进行命名，而认知的不确定性就代表缺乏有关于该模型参数的知识(Parry, 1996).在做事的时候，通过概率风险分析解决偶然不确定性是关键，同时解决认知的不确定性也是至关重要的，对模型的了解可以引导我们做出好的决定。库克（1997）为我们提供了不确定性正确建模的实例。有关模型本身的不确定性也在文献中被讨论，这种不确定性就是可能会考虑利用最接近实际系统替代模型来解决(Nilsen amp; Aven, 2003)。然而，在这篇文章中，我们只考虑第一步，外加考虑认知的不确定性。分析计算的复杂度限制了我们在这点上所要用的时间。

解决认知不确定性，我们可以通过概率统计技术，比如引导或基于可能的方法(Freyamp;Burmaster,1999)，贝叶斯式最为可以处理这两种类型不确定性的方法被广泛接受(Apostolakis, 1978; Cooke, 1991; Hofer,

1996; Hora, 1996; Mosleh et al., 1988).然而，温克勒指出贝叶斯参数分离这些不确定性的类型没有任何根据。汉斯和金兹堡（1996）使用模型、条件的变化来解决不确定性。温克勒的论点，从本质上来说就是事件的变化性纯粹就是我们对将来会发生的事情的无知。

然而，各种不确定性的区别在风险评估的过程中有其特定的重要性的（安德森等人，1999）。具体来说，对于公众和决策者来说，这区别在解释模型结果，收集数据时是至关重要的。在通常表达下，这区别要明确区分“我们不知道这件事是否会发生”和“我们不知道这件事发生的概率”之间的差异。在数据收集环节，认知的不确定性可以随着数据的收集和不断地学习而弥补，可偶然不确定性确是无法消除的，因为它是系统本身所存在的（霍拉，1996）。贝叶斯建模允许有这种区别也处理那些事物本质的区别。在贝叶斯分析技术被用来分析数据和专家判断时，蒙特卡罗仿真可用于通过模型来分析这不确定性（这需要惊人的计算）。

1. 海上风险评估不确定性的建模

我们用一个轮渡系统的案例来证明海上风险评估中不确定分析的应用(Merrick et al., 2003;

van Dorp et al., 2001)。我们就考虑发生在轮渡和其他船舶之间相撞的事故。碰撞引发至一起突发事件，可能是推进器故障、转向失误、导航辅助故障、人为错误、或附近的船只失误（这里我们不一一分解）。这些偶然的失误或错误可能会导致一起碰撞事故，假如纠正措施不能应用成功，这些突发事件其本身就是导致碰撞的诱因。这些事故都发生在一定的条件下，这条件也会影响它们发生的概率。表一就为我们展示了在WSF风险评估中描述当时情况的因素。

3.1 概率风险框架

事故概率模型是建立在条件概率的概念上的，调整那些可能会影响事故发生概率的因素，来估计事故在所给时间段发生的概率，最后总结出那些可能的情况。

P=（1）

其中Situationj表示可能出现情况的因字数，有1、、、、k，k是所有出现概率的总和数，Incidenti就表示突发事件的因子数和出现概率（我们所给例子有五个）。预期的年碰撞频率也可以用公式所得数据乘以一年的时间计算得出。

事故概率模型由三部分组成：

P(Situationj):系统中一些因素概率的特定的总和；

P(Incidenti | Situationj):特定突发事件的概率；

P(Collision | Incidenti, Situationj):事故发生在突发事件已经发生了的情况下的概率。

要用这个模型来进行事故风险评估，这个模型中的每一项概率模型都要事先估计。

这系统模拟就是用于计算不同因素下这种情况的发生量。海上运输系统的模拟系统已被创建来将船舶运动和环境条件相结合，具体化。一个位置算得上是每个模拟的时期都要考虑，就是在那里渡轮可能会涉及到意外事故，至于碰撞情况，它一般发生在一艘船被认为是与一艘渡轮相互影响的时候。在一年的模拟系统运行中，在模拟的每个时期，所有发生的情况都要被计算。因此，这种指定时期内特定因素的情况的发生概率，就定义为P(Situationj), 可以用这个模拟系统被估摸到。使用系统模仿也允许对系统全面的降低风险估价，风险转移的影响与特殊风险干预措施的实施紧密相连。(see, e.g., Merrick et al., 2000, 2002).传统的模拟技术被用于PWS,WSF和旧金山湾的研究，这意味着P(Situationj)的估计值已被获得了。

估计P值的首选方法是通过事故数据统计分析。然而，专家判断启发往往是风险分析中至关重要的（库克，1991）.在PWS和WSF的两件事故的风险分析中，只有低于三个相关事故被记录。因此分析不得不依靠专家判断。这个专家启发的方法的目的，如应用于海上风险，就是去估计影响碰撞概率的多种因素的影响，定义为P(Collision | Incidenti, Situationj).图三所示就是从WSF风险评估项目中得出的问题的格式。

请注意，在每一个比较中，第一种是完全按照事实描述的，专家对比了两种情况，只有一个因素改变了。对这些问题的回复是依据于在这两种情况下事件的相对概率。如果专家圈“1”，这就意味着他相信这两者的可能性将是平等的，如果专家在左边或右边圈的是“9”，就表示他相信比例的概率为9（1/9） (Saaty, 1977)。

潜在概率模型的形式就可以总结为：； （2）

P0是碰撞的基准概率，beta;是一种因子效应参数的向量。由于这形式的选择概率的比例与exp((SituationL minus; SituationR)T beta;)相同。其中SituationL和 SituationR 分别是问题左右两边的情况的因素向量。如果我们将专家回应的自然对数和相应模式项目等同起来，就可以利用线性回归技术进行分析。因此，唯一的点估计值就得到了。还应该注意的是，这可能是用这种方法计算出的1以上的概率（但不低于零），需要截短。然而，虽然模型的形式会允许不相干的标准，但它们是极不同的，因为我们正在处理这方面的低概率事件。

P(Incidenti | Situationj)的测定取决于数据的可用性。而机械故障的数据是现成的，可人为失误的数据确是难以处理的。就意味着，目前我们还没有标准的方法来估计 P(Incidenti | Situationj) 的值，我们将在3、4节这个细节。

图4 展示了一个简单的影响图，关于方程（1）的概率模型和用于估计每个节点下每个条件概率的数据。为了解决在PWS/WSF风险评估方法中的不确定性因素，我们需要一个全面连贯的方法来分别解决P(Situationj)的模拟估计、专家对条件概率的评估之中的不确定性P(Collision | Incidenti, Situationj)、机械与人为失误造成的评估不确定性、还有专家判断所得出的 P(Incidenti | Situationj)，然后我们必须通过方程（1）所得框架来传播这些不确定性。

3.2 模拟不确定性

贝叶斯模拟不同于传统模拟反方式，它的概率分配是用于表示模型参数的不确定性而不是点估计值和置信区间。这种处理被应用于对模型的随机输入与输出。在语言不确定的情况下，经典的仿真模型只有偶然不确定性，而贝叶斯模型却可以同时研究偶然和认知的不确定性。然而，我们应该注意我们所使用的贝叶斯术语类似于奇可（1997），而不是Bier and Andradottir （2000）所使用的，模型输出的数据将会被用于更新决策者对输入输出的分配。我们的目标就像奇可一样，要基于交通数据来更新数据输入分布，通过输入数据的运行得出输出数据，在单独研究。

在贝叶斯模拟中，输入的不确定性应该被纳入分析，以表达有限的数据可以用于填充到达过程中的参数（奇可，2001）。交通流的更新过程贝叶斯模型在2005年被麦里克等人所创建，用以模拟旧金山湾船只的到达过程。在更新过程中，优先考虑的是那些从海岸警卫队船舶交通中心中得到的数据。输入的不确定性是通过使用下列算法的计算累计而得的。所以偶然不确定性只出现在一个算法中，而认知不确定性会出现在多个算法中。输入不确定性的存在就意味着输出不确定性同然。输入不确定性得出的输出数据也将包括认知不确定性和偶然不确定性。在我们的风险评估方法中，从模型中获得的数据就是对其他船舶产生相互作用的数值，就表示为Nr，J为r的复制（r=1，。。。，s就得出s），J就是这些因数的组合值（J=1--K).通过贝叶斯方法我们对输出数据假设一个随机概率模型，并加入我们先前所

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[151595]，资料为PDF文档或Word文档，PDF文档可免费转换为Word