末端接枝银纳米粒子纤维素纳米晶的薄膜制备外文翻译资料
2021-12-20 22:03:10

英语原文共 60 页
目录
9.纳米纤维素基纳米复合材料的力学性能
纳米纤维素的力学性能是其最重要且最有价值的研究。这些性能被大自然广泛应用,因为纤维素的结构使植物细胞拥有更高的力学强度和刚度。纳米纤维素的纳米级尺寸和高长径比使其成为强化聚合物材料的理想选择。为了改善材料的力学性能以及利用这些性质,尤其需要关注复合材料的加工过程。众所周知,非均相材料的宏观力学性能取决于各相特定的行为和成分(各相体积分率),也与形态学(相的空间排列)和界面性质有关。
通常将常规高模量增强剂添加到聚合物中,使复合材料的模量和强度得到改善,而延展性和冲击强度降低。在具有较好分散性的纳米粒子的情况下,可以改善模量和强度而不能改善其延展性,因为其纳米级尺寸不会产生高应力集中。
近年来,人们对于纤维素纳米晶或纤维素纳米微纤(MFC)作为聚合物基质中的增强相开展广泛研究,评估复合材料的力学性能和力学增强效果。动态力学分析(DMA)是研究材料在较宽温度或频率范围内的线性力学行为的有力工具,它对异质系统的形态非常敏感。非线性力学性能通常通过经典的拉伸或压缩测试来获得。
9.1开创性研究
1995年首次证明了纤维素纳米晶增强效应(Favier等,1995a)。不久之后发表了第二篇论文(Favier等,1995b)。在这些研究中,用从被囊类动物提取的纤维素纳米晶增强了乳胶形式的苯乙烯-丙烯酸丁酯共聚物(聚S-co-BuA)。 通过DMA实验研究了纳米颗粒在剪切模式下的增强效果。
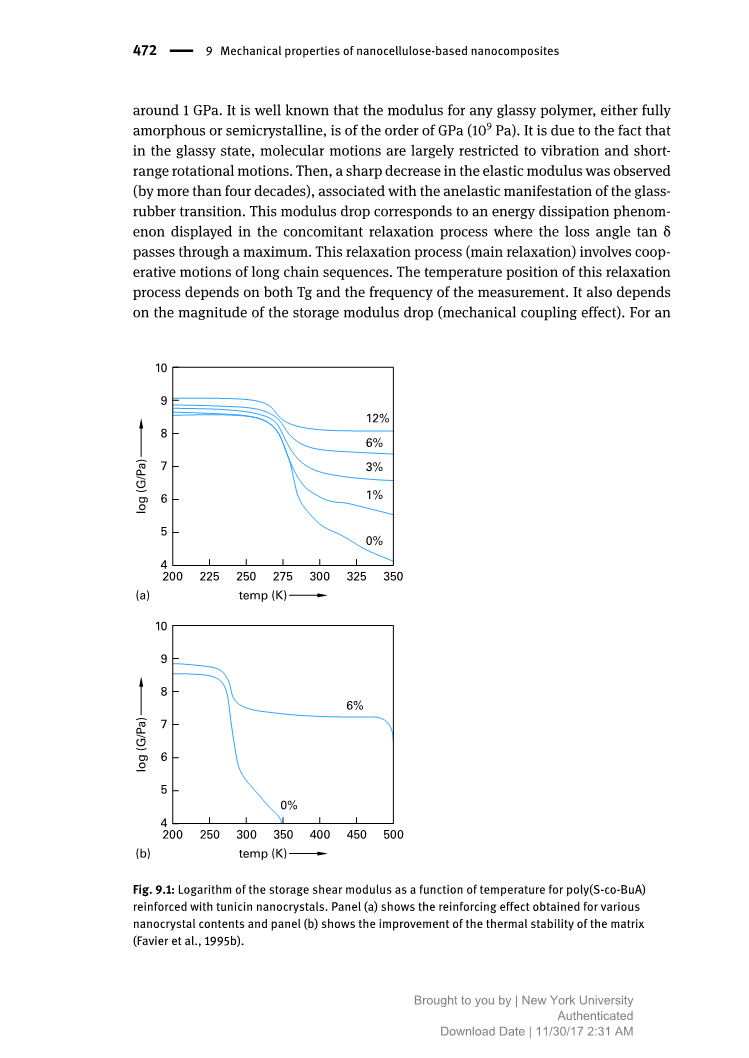
图9.1显示了该系统的储能剪切模量随温度的变化。对应于纯基质的曲线是无定形热塑性塑料的典型曲线。对低于其玻璃化转变温度(Tg),共聚物处于玻璃态并且模量在大约1GPa下大致保持恒定。任何玻璃态聚合物(完全无定形或半结晶)的模量约为GPa级(Pa)。这是因为在玻璃状态下,分子运动很大程度上受限于振动和短程旋转运动。随后弹性模量急剧下降(超过四十年),这与玻璃橡胶过渡的非弹性表现有关。该模量下降伴随弛豫过程中的能量耗散现象,其损耗角tandelta;超过最大值。该弛豫过程(主要弛豫)涉及长链序列的协同运动,其温度取决于Tg和测量频率,还取决于储能模量下降的幅度(力学耦合效应)。对于无定形聚合物,后续橡胶态稳定的温度范围取决于其分子量。在末端区域,随着温度的升高,模量变得更低且结构无法测量,这是由于链解缠引起聚合物不可逆流动。
对于纳米复合薄膜,即使在低含量下将被囊类纤维素纳米晶添加到主体聚合物中后,储能模量也能得到显着改善(图9.1(a))。由于在该温度范围内其力学性能较差,这种增加在热塑性基质的玻璃 - 橡胶转变温度之上尤其显着。在热塑性基质的橡胶状态下,负载水平低至6 wt%的复合材料的模量比未填充的基体高出两个数量级。 此外,引入6 wt%或更多的纤维素纳米晶提高了基质模量(图9.1(b))和热稳定性,可达到纤维素开始降解的温度(500K)。
图9.1:用被囊纤维素纳米晶增强的聚S-co-BuA的储能剪切模量的对数随温度的变化。
图(a):不同含量纳米晶的增强效果;图(b):基质热稳定性的改善(Favier等,1995b)。
9.2 力学增强模型
与纤维素纳米微纤(MFC)相比,纳米纤维素增强纳米复合材料的力学性能的模型更容易用纤维素纳米晶建立,因为其具有更明确的形态。在多相聚合物体系中,力学性能取决于各相的特定行为,组成(每相的体积分数)、形态(相的空间排列)和界面性质。对于非均质材料,弹性模量与各参数之间的关系已得到广泛研究。其中一个最简单的模型涉及组分的串联(Reuss预测)或并联(Voigt预测),并对应模量的下界和上限。它分别指各组分柔度和模量的混合规则。 无论二元系统的形态如何,实验模量值都在这两个极限之间。
9.2.1平均场方法
在对被囊纤维素纳米晶增强苯乙烯-丙烯酸丁酯共聚物(聚S-co-BuA)的开创性研究中,从纳米颗粒的高模量出发,试图了解纳米颗粒在高温下所具有的不同寻常的增强作用。使用Halpin-Kardos(Halpin和Kardos,1972)的理论模型对这些纳米复合材料的力学性能进行建模,该模型已被广泛用于预测短纤维复合材料和半结晶聚合物的弹性剪切模量。选择该模型是因为其简单性和粘弹性。 Halpin-Kardos模型被称为平均场方法的“上键”。值得注意的是,对于温度大得多或远低于Tg的温度,力学性能可以在第一次估算中被认为是弹性的。实际上,模量的损耗分量比弹性模量低10倍以上,因此仅考虑弹性行为。在该平均场方法中,假设纤维分散在基质中以形成均匀的连续体。该复合材料可视为“准各向同性”的材料,由四层定向层(0°,45°,90°和-45°)构成(如图9.2)。
图9.2:在Halpin-Kardos模型中具有四层取向填料(0°,45°,90°,-45°)的复合材料的示意图。
随着不同等角度层取向的数量增加,力学性能变为各向同性。 单层(单向短纤维)的力学性能由Halpin-Tsaiuml;微观力学方程(“自洽”迭代方法)给出(Tsaiuml;等,1968):
(i=1,2)
(9.1)
其中是纤维方向的刚度,是垂直于纤维方向的刚度估算值,是面内剪切模量估算值,phi;是纤维体积分数。 下标m和f分别指代基质和填料。 填料的几何形状通过xi;参数来处理,其中L、l和e分别是纤维的长度,宽度和厚度。 对于棒状的纤维素纳米晶,l = e = d为纳米晶体的直径,并遵循(Halpin和Kardos,1972):
xi;=2·
xi;=2· (9.2)
单向层的工艺常数如下:
(i=1,2)
(9.3)
从而有以下表达式:
(9.4)
然后,通过下式给出“准各向同性”层压板的拉伸模量,假定接近于短纤维复合材料的拉伸模量。
(9.5)
泊松比近似由混合规则给出:
(9.6)
在该方法中,复合材料的预测性能取决于填料的尺寸,形状和体积分数以及基质和纤维的力学性能,包括填料的力学各向异性。 因此,考虑纤维素纳米晶体的高模量,但不考虑纤维之间的相互作用。(如图9.2)
该模型已用于预测用被囊纤维素(Favier等,1995a; Hajji等,1996)和小麦秸秆(Helbert等,1996)纤维素纳米晶体增强的聚S-co-BuA纳米复合材料的力学行为, 以及用被囊纤维素纳米晶体增强的聚氯乙烯(PVC)(Chazeau等,1999a)。 计算中使用的参数见表9.1。
表9.1:用于Halpin-Kardos模型的纤维素纳米晶和聚合物基质的力学参数。
纤维素纳米晶的力学性能见表1.4。 长径比(L / d)可以从显微镜观察取平均,对于玻璃态结晶下的纤维素,泊松比取0.3。 实验表明,聚合物基质的泊松比在橡胶态下为0.5,在玻璃态下为0.3-0.35。 因此除了Hajji等人之外,没有人使用可调参数以调整长径比满足实验数据。
研究表明,预测的橡胶模量未能描述实验数据。复合材料的玻璃态模量被高估,而橡胶态模量被低估(Helbert等,1996; Chazeau等,1999a)。然而,在拉伸试验得到的基质玻璃态模量值与数据基本一致(Hajji等,1996)。对晶须填充聚合物和平板填充聚合物的潜力进行了数值模拟,结果表明,广泛应用的Halpinminus;Tsaiuml;方程系统地低估了这些材料的实际潜力。(Gusev,2001)。除了纳米粒子的长径比之外,很难质疑Halpin-Kardos预测中使用的参数。实际上,有人提出纤维素纳米晶体可以连接在一起形成更长的实体或纳米粒子串。以麦秸纤维为原料制备纳米晶,以长径比为可调参数,实验数据拟合成功,长径比为450,比形态观测值高10倍(Helbert等, 1996年)。因此怀疑是力学渗透现象。
9.2.2渗透方法
统计几何模型的渗流一词于1957年首次提出(Hammersley,1957)。该统计理论可以应用于涉及大量可能有联系的物种的系统,其目的是预测未完全连接的一组对象的行为。通过改变连接的数量,该方法允许描述从本地到无限“通信”状态的转换。逾渗阈值定义为分离这两种状态的临界体积分数。粒子的相互作用(Balberg和Binenbaum,1983)、取向(Balberg等,1984)或长径比(de Gennes,1976)都可以改变逾渗阈值。使用这种方法来描述和预测纤维素纳米晶基于复合材料的力学性能表明,纳米晶形成的刚性网络是在高温下观察到的异常增强效应的原因。模型包括三个重要步骤:
- 第一步确定逾渗阈值(vRc)。 对于圆柱形颗粒,根据它们的长径比和纳米晶的有效骨架,可以使用统计渗透理论计算几何渗透所需的纤维素纳米颗粒的体积分数(Favier等,1997a)。 在位置和取向上随机生成5000个三维棒,对连接试样两侧的纳米粒子的无限长分支可能存在的交点进行了研究。结果表明,当增大长径比时,达到几何渗流所需的临界体积分数急剧减小。从而确定如下关系:
(9.7)
对于长径比为67的纳米棒,例如被囊类纤维素晶体,则需要约1%的体积分数来实现三维几何渗透。 该计算可以通过消除有限长度分支来帮助识别纳米晶体的有效骨架,即那些有效地属于无限长度分支的骨架。 对于长径比为45的麦秆纤维素纳米晶体,发现vRc值为约2vol%(Dufresne等人,1997)。可以证明,非均匀长度分布计算的逾渗阈值低于均匀长度分布计算的逾渗阈值(Balberg和Binenbaum,1983)。
然而,渗透的概念看起
资料编号:[4172]




