地震作用下桥梁横向挡块抗水平推力极限承载力计算与分析毕业论文
2020-02-19 16:21:18
摘 要
本文研究在地震力作用下桥梁横向挡块的极限承载力。总结国内外研究人员对桥梁横向挡块承载力极限值的计算方法和研究成果。通过手工计算和有限元软件模拟计算对比不同桥梁横向挡块在水平力作用下的极限承载力,分析影响桥梁横向挡块极限承载力的因素,为桥梁横向挡块设计提供理论依据。研究发现:桥梁横向挡块的水平承载力极限值与挡块的宽度、挡块的配筋方式、水平力施加的位置等因素有关。
关键词:桥梁横向挡块;水平承载力极限值;
Abstract
In this paper, the ultimate bearing capacity of bridge transverse block under seismic force is studied. This paper summarizes the calculation methods and research results of the ultimate bearing capacity of bridge transverse retaining blocks by researchers at home and abroad. Through manual calculation and finite element software simulation, the ultimate bearing capacity of different bridge transverse retaining blocks under horizontal force is compared, and the factors affecting the ultimate bearing capacity of bridge transverse retaining blocks are analyzed, which provides a theoretical basis for the design of bridge transverse retaining blocks. It is found that the ultimate horizontal bearing capacity of bridge transverse block is related to the width of the block, the reinforcement mode of the block and the position of the horizontal force applied.
Key words:Bridge transverse block;The ultimate value of horizontal bearing capacity
目 录
第1章 绪论 1
1.1 研究目的及意义 1
1.1.1 研究目的 1
1.1.2 研究意义 1
1.2 国内外研究现状 1
1.2.1国外研究现状 1
1.2.2国内研究现状 2
1.3 研究基本内容 2
1.4 技术路线 2
第2章 国内外挡块抗水平推力极限承载力计算公式 4
2.1郑万山、唐光武团队研究成果 4
2.2徐略勤、李建中团队研究成果 5
2.3 国外规范中对桥梁挡块设计要求 9
第3章 横向挡块抗水平推力承载力的影响因素 12
第4章 建立挡块模型与水平推力极限承载力理论值计算 14
第5章 建立有限元模型及挡块抗水平推力极限承载力计算 19
第6章 总结 31
参考文献 34
致 谢 36
第1章 绪论
1.1 研究目的及意义
1.1.1研究的目的
桥梁横向挡块也称桥梁外剪力键,是设置在桥墩盖梁两侧和桥台干墙两侧限制桥梁梁体横向位移,防止桥梁在地震力作用下产生梁体横向偏移甚至落梁的桥梁横向抗震装置。桥梁横向挡块广泛的应用于中小跨径桥梁之中,设计良好的桥梁横向挡块可以有效抵抗桥梁主梁在地震力作用下产生的水平力,限制主梁在地震力作用下的水平方向的位移,以减小桥梁在地震力作用下受到的损伤,从而达到地震后桥梁能快速维修并使用的目的。然而,在我国现行的桥梁抗震规范中,桥梁横向挡块设计没有得到足够的重视,往往依靠设计人员、施工人员的从业经验来设计。所以往往当地震真正发生时,桥梁横向挡块并不能真正承担起桥梁减隔震的作用,往往在地震作用下横向抗震混凝土挡块受损严重,桥梁主梁产生横向位移乃至于落梁。在2008年中国汶川大地震中,有超过几千座桥梁收到了严重损害,在这之中有很大一部分是桥梁不同程度的横向位移,混凝土挡块不同程度的损坏,损坏严重的更是发生了落梁这一现象。这些桥梁震害实例充分说明了合理设置桥梁横向混凝土挡块的重要性,也暴露了我国现行桥梁抗震规范中对桥梁横向混凝土挡块设计要求不够完善的问题。因此,研究桥梁横向挡块抗水平推力极限承载力有助于为我国桥梁横向挡块设计提供理论依据及技术支持,有助于对现行规范进行完善。
1.1.2研究的意义
本文对目前世界上各国的桥梁抗震设计规范中横向混凝土挡块抗水平推力极限承载力部分做了归纳总结。结合国内研究人员对我国桥梁横向抗震混凝土挡块的研究,分析影响桥梁横向混凝土挡块抗水平推力极限承载力的因素,总结归桥梁横向混凝土挡块抗水平推力极限承载力的计算方法,建立桥梁横向混凝土挡块有限元模型,着重分析水平推力作用位置以及挡块宽度对桥梁横向混凝土挡块抗水平推力横向承载力极限值的影响,分析横向挡混凝土块抗剪承载力的加强措施,为桥梁横向混凝土挡块的抗震设计提供理论参考。
1.2国内外研究现状
1.2.1国外研究现状
国外对桥梁横向抗震混凝土挡块的研究较早,在美国混凝土结构设计规范acl318、结构混凝土建筑规范要求(ACI318-71)和美国加州桥梁抗震规范Caltrans 规范中规定了桥梁混凝土挡块的设计抗水平推力承载力极限值和混凝土挡块抗水平推力承载力的计算方法,为横向挡块设计提供了理论依据和明确要求。在日本道路桥示方书中,也给出了桥梁落梁防止装置抗水平推力极限承载力的计算方法。
1.2.2国内研究现状
国内研究人员结合国内外桥梁抗震规范、国内桥梁横向混凝土挡块破坏实例,在国外计算方法的基础上提出改进,为我国桥梁抗震设计规范提出参考意见和计算方法。本文主要总结归纳了郑万山、唐光武团队和徐略勤、李建中团队对桥梁横向挡块极限承载力研究成果。
1.3研究的内容
本文总结了国内外研究人员对桥梁横向挡块的研究成果和桥梁横向挡块极限承载力计算公式,建立挡块的有限元模型。对挡块模型分别进行手工计算及软件模拟计算其抗水平推力极限承载力,并对比分析影响挡块抗水平推力极限承载力的因素。
具体内容和章节安排如下:
第1章:绪论。主要介绍本文的研究背景、目的、意义,国内外的研究现状、本文的研究内容。
第2章:国内外研究现状。主要总结归纳了国内外桥梁设计规范、研究论文对桥梁横向挡块抗水平推力极限承载力的要求及计算方法
第3章: 横向挡块抗水平推力承载力的影响因素。根据国内外规范、研究论文对桥梁横向挡块抗水平推力极限承载力的计算公式分析可能的影响桥梁横向挡块抗水平推力极限承载力的影响因素
第4章:建立挡块模型与水平推力极限承载力理论值计算。根据上一章所得可能影响挡块抗水平推力极限承载力的因素,控制变量,建立挡块模型并计算所建立挡块模型的抗水平推力极限承载力。
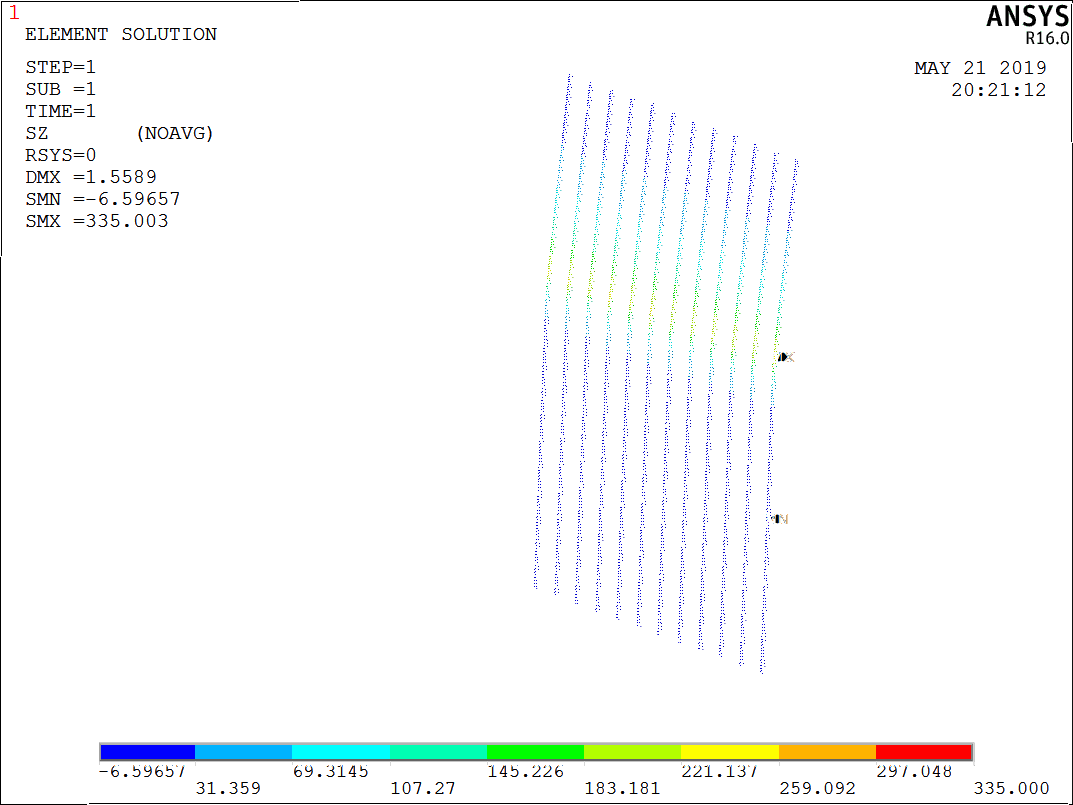
第5章:建立有限元模型及挡块抗水平推力极限承载力计算。根据上一章所建立的模型,在ansys软件中建立相应的有限元模型,并通过计算机求解挡块抗水平推力极限承载力
第6章:结论。对比分析挡块抗水平推力极限承载力理论计算值与软件模拟值,总结不同影响因素对挡块抗水平推力极限承载力的影响。
1.4技术路线
本文借鉴国内外研究成果、国内外技术规范,结合ansys有限元软件建立不同桥梁横向挡块模型。通过手工计算和软件模拟计算,求解桥梁横向挡块抗水平推力极限承载力,对影响桥梁横向挡块抗水平推力极限承载力的因素进行对比分析,为桥梁横向挡块设计提供参考。
第2章 国内外挡块抗水平推力极限承载力计算公式
2.1郑万山、唐光武团队研究成果
我国现行的规范中对横向挡块抗水平推力极限承载力值并没有非常明确的计算公式和计算方法,但国内许多研究人员通过对地震灾害中桥梁受损混凝土挡块的分析研究以及对国外规范的研究改良提出了计算混凝土挡块抗水平推力承载力最大值的方法,为桥梁横向挡块抗震设计提供了参考,为桥梁抗震规范的改进提供了理论依据和数据支持。
郑万山、唐光武等以我国四川汶川地震受影响桥梁横向抗震混凝土挡块为原型,通过改变混凝土挡块的箍筋形式(包括封闭式箍筋和非封闭式箍筋)、挡块长度、挡块宽度、挡块高度、挡块配筋率、挡块配箍率等变量,建立了五个桥梁横向混凝土挡块受力模型。对我们国家常见的桥梁横向挡块形式进行了拟静力试验研究、分析其破坏机理,并提供了桥梁横向挡块抗水平推力极限承载力的计算公式:
对于封闭式箍筋的混凝土挡块(混凝土挡块箍筋方式如图1),挡块的破坏形式均是在挡块根部产生弯曲破坏,形成先弯后剪的破坏特征,可以采用下列公式(1-1)计算桥梁横向混凝土挡块抗水平推力极限承载力
(1-1)
上式中,是桥梁横向挡块抵抗上部结构作用的水平推力的极限承载力,单位为N; H为上部结构作用在挡块的水平推力到盖梁顶面的距离,单位为cm; L 为挡块内侧纵筋距离挡块受压区中心的距离,单位为cm;为挡块内侧竖向钢筋抗拉强度标准值,单位为MPa; As为挡块内侧竖向钢筋面积,单位为。
对于非封闭式箍筋的混凝土挡块(箍筋方式如图2所示),其本质上并不是箍筋,而是分布钢筋,该种混凝土挡块的抗水平推力极限承载力较小,其破坏特征表现为脆性破坏,由于该挡块没有抗剪腹筋,可按下列公式(1-2)计算其抗水平推力极限承载力 :
=·b·h (1-2)
上式中,为混凝土抗拉强度标准值,单位为MPa; b 为挡块厚度,单位mm; h 为挡块长度,单位为mm。
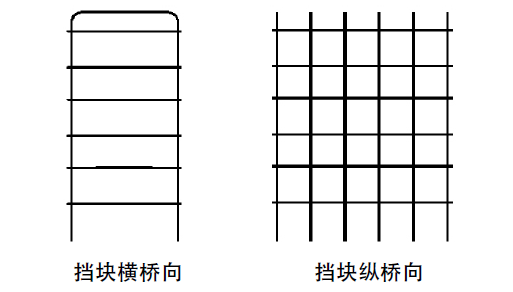
图 1封闭式箍筋
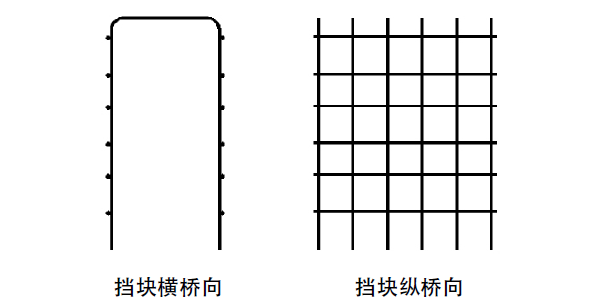
图 2非封闭式箍筋
2.1徐略勤、李建中团队研究成果
徐略勤、李建中等针对目前桥梁横向挡块抗震能力低下的现象,提出了一种新型的滑移挡块,并与常规混凝土挡块进行对比,提出两种挡块抗水平推力极限承载力的计算方法。对于常规混凝土挡块,可以分别计算桥梁横向挡块中混凝土分项和钢筋分项对于挡块抵抗水平力和变形的贡献,得出了如下图3所示的简化分析模型。
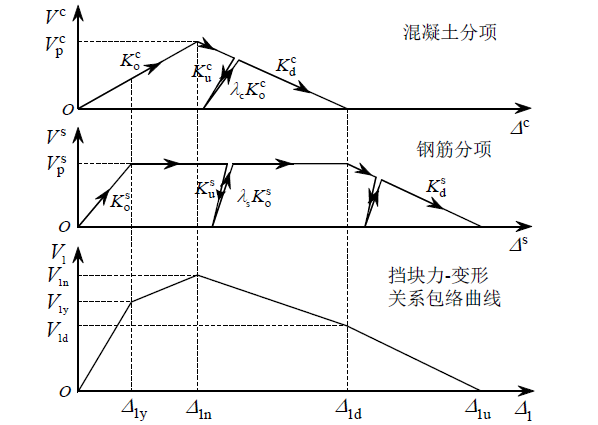
图 3常规挡块简化分析模型
在上图所示的混凝土分项中,混凝土分项所受到的剪力与挡块位移成正比,挡块位移越大,混凝土所受的剪力值越大,直至裂缝贯通。当裂缝贯通时,混凝土的剪力传递面积最大,剪力相应出现最大值。随着裂缝宽度进一步的扩大,在混凝土的开裂面上混凝土的摩擦效应和骨料间咬合作用逐渐被削弱,剪力会不断的下降直至完全消失。因此,混凝土分项弹剪力与挡块变形 的关系可描述为:当时,混凝土分项的剪力成正比,比例系数为;在挡块变形达到时,混凝土分项的剪力值达到最大值,随着挡块变形的进一步增大,在挡块变形处于至之间时,混凝土分项的剪力按如下公式计算:=-()(1-3);当挡块变形超过后,混凝土不承担剪力,剪力值0
对于弹簧分项承担的剪力先是随着挡块位移的增大而增大,然后剪切钢筋达到屈服状态,当剪切钢筋屈服时,钢筋部分提供的剪力承载力达到最大值。最后,在水平力的作用下剪切钢筋会遭到破坏,由钢筋提供的抗剪力逐渐下降直至为0。因此可将钢筋分项的剪力与挡块变形的关系描述为:在挡块变形处于0到挡块屈服变形之间时,钢筋分项承担的剪力值与挡块变形成正比,比例系数为;当挡块变形到挡块屈服变形时,钢筋分项承担剪力达到最大值,在挡块位移处于挡块屈服变形到挡块退化变形之间时,钢筋承担剪力进入一个最大值平台。随后,随着挡块位移的进一步增大,钢筋受力破坏,导致钢筋分项承担的剪力逐步减小,最终在挡块达到极限变形时由钢筋分项提供剪力也下降为0,整个挡块完全破坏,不再提供抗水平推力。
对整个混凝土挡块而言,其挡块变形随着水平推力的不断增加,首先发生屈服变形阶段,然后是名义变形阶段和退化变形阶段最后达到极限变形阶段。在这四个阶段的三个转折点上,表示为挡块的屈服强度、表示为挡块的名义强度、表示为挡块的退化强度。
对于不同的混凝土挡块破坏形式,的取值可按照不同的计算公式求得,对于混凝土挡块沿斜截面破坏的这一形式,可以把挡块本身看作一个刚性体,以斜截面与外侧交点O点为圆心,挡块在水平推力的作用下绕O点旋转。通过实验的模拟和地震破坏的实例,挡块破坏时一般产生与水平方向呈45°角的贯通裂缝,在裂缝区域内的剪切钢筋与水平抗拉钢筋呈现完全屈服的状态。在裂缝范围内的盖梁前后两个表面的水平构造筋也都呈现屈服状态;盖梁内竖直方向的箍筋没有达到屈服值且受力很小,因而可以看作竖直方向箍筋不受力。据此本文采用如图4 所示的挡块模型用以模拟混凝土挡块沿斜截面剪切破坏时的状态。
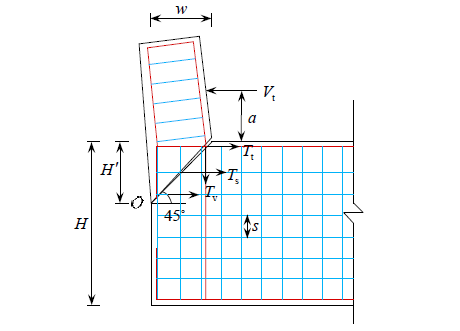
图 4斜截面转动刚体模型
针对这一模型,挡块的抗水平推力极限承载力主要来自裂缝范围内混凝土提供的抗水平推力值,以及裂缝范围内钢筋(包括剪切钢筋、水平拉筋和水平构造筋)提供的抗水平推力值两部分,。因此,挡块的抗水平推力承载力极限值包含上述两部分之和:
= (1-4)
根据Priestley等人的研究成果,挡块混凝土部分贡献的抗水平推力值Vc/N,可采用如下的公式:
Vc =0.2 bH=0.2bw(1-5)
式中:fc是混凝土的轴心抗压强度,其单位为MPa。b为挡块的厚度,单位为mm H为盖梁裂缝区域的竖向高度,单位为mm。w为挡块的宽度,单位为mm。钢筋的剪切贡献强度Vs,单位为N。 可通过转动刚体的平衡原理求得。如图4,所有参与挡块强度贡献的钢筋对O点取矩,并依据挡块隔离体的平衡关系可得:
=(a H)=H w [(H-s) …… ](1-6)
式中:s为穿过开裂面且靠近O 点的最下排水平构造筋与 O 点间的竖向距离,近似取 =s ,而H=w,且通常水平构造筋的面数=2,将各钢筋拉力计算公式带入上式,得如下两式:
(a H)= (-1)(1-7)
=[ ()]()(1-8)
式中:a为加载点距底座顶面的高度,单位为mm 。s为水平构造筋的间距,单位为mm。和分别为剪切钢筋的总面积及其屈服强度,其单位分别为和MPa,由图4可知倒U型剪切钢筋只有内侧分肢有贡献,因此式(1-2)中取1/2;/mm2 和 /MPa 分别为穿过开裂面的水平拉筋的面积及其屈服强度;As/mm2 和fys/MPa 分别为穿过开裂面的单根水平构造筋的截面积及其屈服强度。
将式(1-5)(1-8)代入式(1-4)可得混凝土挡块抗水平推力极限承载力计算公式(1-9)
=0.2bw [ ()]() (1-9)
对于沿连接面转动的混凝土刚体模型,混凝土横向挡块可看作一个刚性体在水平推力的作用下绕圆心O点旋转。根据实验模拟结果和破坏实例,贯通主裂缝近似沿挡块底部与盖梁顶部的水平面延伸。内侧的竖向剪切钢筋都发生了屈服,而水平方向的构造钢筋和水平方向的拉筋大都处于弹性状态。盖梁部分的混凝土没有出现裂缝。由此,本文采用如下图5所示的桥梁横向挡块沿连接面转动刚性体模型。下图中a为双排布置剪切钢筋的桥梁横向混凝土挡块, b为单排布置剪切钢筋的桥梁横向混凝土挡块。由图5可知,桥梁横向挡块的抗水平推力承载力值主要由混凝土在裂缝区域传递的剪力值Vc,以及裂缝区域钢筋贡献的剪切值Vs。挡块的抗水平推力承载力值Vn 可采用式(1-4)表示。混凝土贡献的抗水平推力承载力Vc单位为N,Vc =0.2bw。钢筋贡献的抗水平推力承载力Vs/N ,主要来自穿过裂缝区域的剪切钢筋Tv。根据刚体平衡原理可得:
剪切钢筋双排布置时:
= =bw(1-10a)
剪切钢筋单排布置时:
= =bw (1-10b)
其中:(单位为mm),为剪切钢筋内侧分肢与挡块外侧面的水平距离;为剪切钢筋率=/bw;其余符号意义同前。将式(1-10a)、(1-10b)、(1-5)分别代入式(1-4)可得混凝土挡块抗水平推力极限承载力值计算公式。
当双排布置剪切钢筋时:
=(0.2)bw (1-11a)
当单排布置剪切钢筋时:
=(0.2)bw (1-11b)
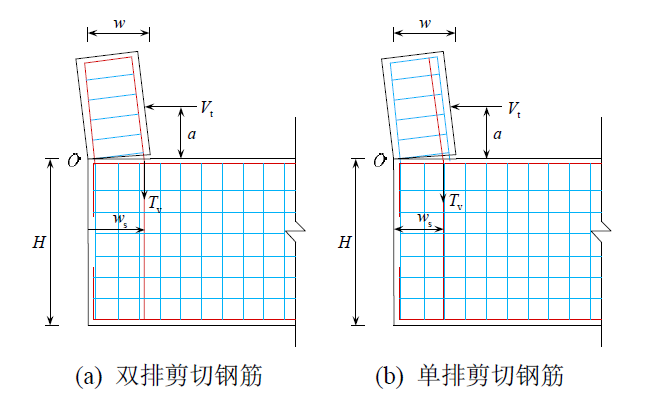
图 5沿连接面转动刚体模型
2.3国外规范中对桥梁挡块设计要求
国外对于桥梁减隔震设计的研究较早,并且在现行的规范中提供了计算挡块抗水平推力极限承载力的相关公式及方法。其中以美国和日本尤为详细和规范。结合国内、国外各种桥梁震害实例和研究表明,混凝土挡块抗水平推力极限承载力的设计大小不宜过大也不宜过小。如混凝土挡块抗水平推力极限承载力设计得非常大,可能导致桥墩在地震作用下更易于破坏,如混凝土挡块抗水平推力极限承载力设计得非常小,其限位作用可能不能够完全发挥,最终导致桥梁落梁,因此合理确定混凝土挡块的设计强度在混凝土挡块设计中至关重要。
根据美国Caltrans 抗震规范的相关要求,横向挡块的设计抗水平推力承载力最大值应当遵守于如下公式进行计算否则可能导致桥墩在地震作用下更容易破坏:
min(0.75×Σ0.3×)
上式中,为挡块设计抗水平推力极限承载力;为桩的横桥向剪切能力;为桥墩所承受的恒载竖反力。
国外对于不同混凝土挡块的破坏模式,给出了不同的抗水平推力承载力计算方法。主要有如下三种分析模型:拉压杆模型、剪切摩擦模型、抗弯承载模型。在这三种模型之中,美国混凝土结构设计规范acl318采用剪切摩擦模型来计算混凝土构件开裂面处传递的剪切力。基于对该模型的理论计算和实际使用,许多学者对该模型提出了改进,提出了新的计算混凝土构件剪切强度的计算公式。例如美国加州桥梁抗震规范Caltrans 规范采用下列公式来估算钢筋混凝土挡块的抗剪强度:
Vn=u()0.2
式中,u 为混凝土构件的摩擦系数,预留粗糙的干施工缝混凝土构件取u为1.0λ,对于整体浇注的混凝土构件取u为1.4λ,预留光滑的干施工缝混凝土构件取u为0.6λ,系数λ 对于普通混凝土取1.0;表示穿过剪切面的钢筋面积表示穿过剪切面的屈服强度; 分别表示混凝土抗压强度表示穿过剪切面的面积。
而Mattock的研究认为:混凝土建筑规范(ACI318-71) 中的剪切摩擦公式的计算结果偏小,他使用粘聚力项对该模型进行修正。根据他的理论,裂缝区域所传递的剪切力共有两个部分:一个是上下两个剪切面之间由于钢筋滑移而产生的拉力导致的摩擦;二是上下两个剪切面之间粗糙产生的摩擦。根据Mattock 所提出的模型,普通混凝土裂缝区域传递的剪力可用下述公式计算:
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: