英语原文共 10 页，剩余内容已隐藏，支付完成后下载完整资料

复合钢-混凝土曲线箱梁桥的荷载横向分布

S.J. Fatemi，M.S. Mohamed Ali, A.H. Sheikh

阿德莱德大学土木、环境与矿业工程学院，阿德莱德，SA5005，澳大利亚

文章信息：

文章历史：

2015年5月31日，收到

2015年8月14日，修订表格

2015年8月28日，收纳

2015年9月15日，传于网络

摘要：

在澳大利亚桥梁设计规范和美国国有公路运输管理员协会（AASHTO）的推荐下，针对荷载作用下的钢-混凝土组合箱梁桥的水平曲线的荷载分配机理，进行了数值模拟研究。在本次研究中，考虑了诸多影响因素，诸如：曲率比、跨度长度、加载车道数和单元数；此外，为了保持这些结构的最大扭转刚度，进行了收敛性研究，以确定适当的支撑系统。数值模型首先验证实际测试结果，使他们对采用广泛的参数研究具有良好的信心。参数研究的结果被用来确定水平曲线箱梁桥的弯矩和剪力荷载分配系数。据研究，根据AASHTO得到的这些载荷分布因子比由澳大利亚桥梁设计规范推荐的载荷分布因子高得多。这是不合理的使用基于AASHTO载荷分布系数。

爱思唯尔有限公司版权所有 2015

关键词：钢-混凝土混合面板；荷载分布因素；曲线梁桥；支架间距；有限元分析

1. 介绍

水平曲线钢-混凝土组合箱梁在公路桥梁施工中得到了广泛的应用。这种结构体系由一个钢箱截面梁和混凝土桥面板组成，具有很高的抗扭刚度，对抵抗结构曲率产生的扭转效应是很重要的。通常应用在人口高度密集的路口和城市高架公路，这些有空间限制的高速公路线，需要一种弯曲的几何曲线。准确地分析这些复杂的结构是非常具有挑战性的。为了简化分析，一些研究人员试图将复杂的桥面结构简化为一个简单的结构体系，如格栅等效正交异性板和一些其他形式的[ 1-3]。但解的精度影响了这些简化，可能无法使其成为一个可靠的结构模型，被结构设计者接受。其中一个令人满意的结果，可以通过使用一个详细的有限元建模[ 4-10] 这些弯曲的结构，但这是不可行的在设计室，尤其是，进行初步的结构设计。

通常，设计师把这样一个复杂的桥面结构作为单跨梁计算内力如弯矩、剪力和扭矩作用于桥面的整个横截面。这可能适用于一个简单的简支直梁，但这不适用于曲线梁，因为他们总是是超静定的。虽然一些研究人员[9,11,12]尝试避免曲梁本身属性，等效为直梁加构件曲率来代替这种属性。这些简化的假设在精度方面有很大的调控空间，这可能是不可取的。此外，加载配置建议的桥梁设计代码由多个负载作用于结构。在这种情况下，影响线图，这些结构内力的使用估计在桥面临界截面的内力最大值有用。这个问题是由作者在以前的研究[ 13 ]。为了确定超静定曲梁的影响线图，开发了一种封闭形式的解析解（13）。

在下一步中，按照通常的设计技术，设计师需要知道的应力或内力的不同成分或梁等设计各个组件。负载分布因子通常用于根据总剪切力，弯矩和扭矩作用在整个桥梁横截面上计算各个部件的应力集中度。负荷分布因子的有效性肯定可以使这些复杂结构系统的分析和设计容易，但是这些分布因素的确定是相当具有挑战性的。 这些弯曲桥面结构的详细有限元分析可以用于此目的。 这些尝试是由一些研究人员[4-10]进行的，他们使用了AASHTO推荐的装载配置[14]。在他们的调查中，不同参数的影响，如跨度长度，曲率比，跨框间距和加载车道数量 对水平弯曲桥梁的载荷分布因子进行了研究。 已经发现，曲率比和跨度长度是影响这些分布因子的最有影响力的参数。

AASHTO [14]还给出了这些弯曲桥梁结构的载荷分布因子。 然而，根据一些研究人员[8,9,15-17]，这些分布因子被认为是保守的，他们通过物理测试，分析和数值结果验证了这些因素。 此外，任何其他代码（如澳大利亚桥梁设计规范AS 5100.2-2004 [18]）推荐的装载配置（载荷数量，载荷数量和位置）与AASHTO有很大的不同。 因此，根据AASHTO负载配置的负载分配系数不能简单地用于在澳大利亚等其他国家设计桥梁。 因此，需要确定澳大利亚桥梁装载的载荷分布因子（AS 5100.2-2004）。

在本研究中，水平弯曲钢筋混凝土复合箱梁桥梁的载荷分布因子是根据澳大利亚桥梁荷载[18]确定的。首先，对大量弯曲桥面进行了详细的有限元分析。所有的桥梁部件都被建模为壳体元件，除了用作梁梁元件建模的顶部法兰（用于连接混凝土板和钢腹板的钢板的窄条）之外。最初，确定交叉支撑的最大间距，这将不允许任何局部变形并保持弯曲箱梁甲板系统的最大扭转刚度。有限元分析得到的数值结果用实验结果验证[4]，以评估有限元模型的性能。在对有限元建模技术的可靠性获得信心之后，通过使用澳大利亚桥梁载荷，通过改变不同参数，例如曲率比，跨度长度，单元数目和加载车道数量，对180个不同的弯曲桥模型进行了广泛的参数研究组态。

从这些分析中可以得出各个部件或大梁处的最大应力或应力结果。 另一方面，由作者[13]开发的弯曲梁影响线图的闭式解析解被用于计算由于相同的载荷构造而在整个桥面上作用的应力结果。 使用从单个梁的有限元分析获得的应力结果和从分析溶液获得的总应力结果作为它们之间的比率来计算负载分布因子。

基于从这些分析产生的大量数据，进行多变量回归分析以开发经验表达式以确定负荷分布因子。 MATLAB [19]还开发了一个计算机代码来实现回归分析。这些表达式将被设计人员方便地用于单个桥梁的初步设计。 同样的建模技术也用于确定直钢混凝土复合箱梁桥面的载荷分布因子。 最后，将水平弯曲桥梁的载荷分配机理与直箱梁板甲板的载荷分配机理进行了比较。 这些桥面板承受两种不同的桥梁设计荷载，如AASHTO和AS 5100.2-2004。 显示了所获得的弯曲和直线桥面载荷分布因子之间存在显着差异。

2. 水平弯曲梁的分析解决方案

图1. 简支水平弯曲梁

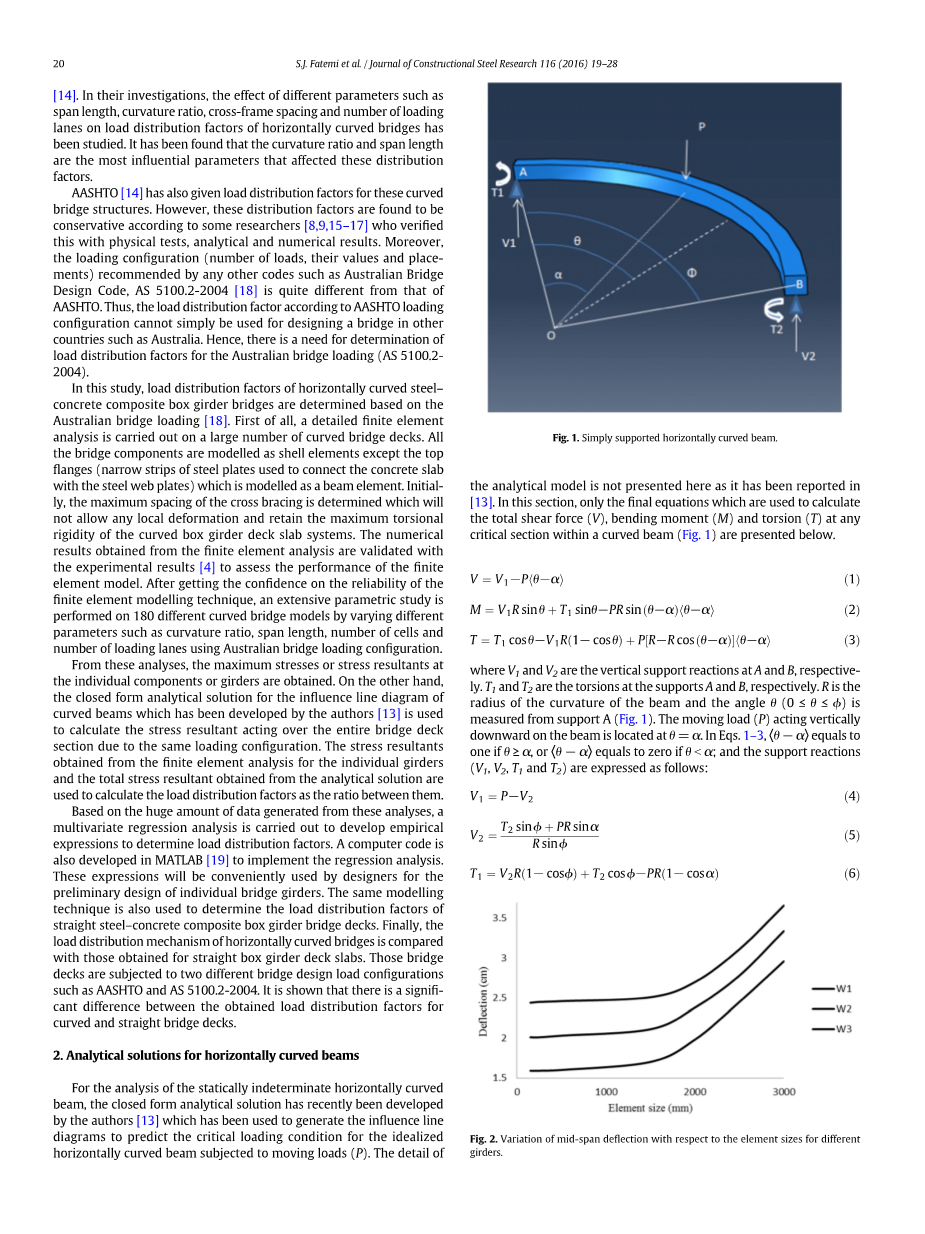
对于静态不确定的水平弯曲梁的分析，封闭形式的分析解最近由作者[13]开发，已经用于产生影响线图，以预测受到理想化的水平弯曲梁的临界载荷条件 移动载荷（P）。 分析模型的细节不在这里，因为它已经在[13]中报道。 在本节中，仅在用于计算弯曲梁（图1）中任何临界部分处的总剪切力（V），弯矩（M）和扭转（T）的最终方程如下。

其中V₁和V₂分别是A和B处的垂直支撑反应。 T₁和T₂分别是支撑件A和B处的扭转。 R是光束曲率的半径，从支架A（图1）测量角度theta;（0le;theta;le;phi;）。 在梁上垂直向下作用的移动载荷（P）位于theta;=alpha;。 在等式 1-3，如果theta;ge;alpha;，（theta;-alpha;）等于一，如果theta;﹤alpha;，（theta;-alpha;）等于零; 支持反应（V₁，V₂，T₁和T₂）表示如下：

偏移（cm）

单元尺寸（mm）

图2. 相对于不同大梁的元件尺寸的中跨偏差的变化。

表1 60 m水平弯梁箱梁桥梁跨距偏移分析

其中

应该注意的是，剪切力的影响线在梁的两端（支撑）处具有最大值，而弯矩的影响线的最大值将发生在梁的中间[13]。

3. 弯曲桥面的数值模拟

水平弯曲箱梁桥系统的数值模拟采用市售有限元软件（ABAQUS）[20]进行。在箱梁桥梁建模过程中，作出了一些假设，使数值模型成为目前实际桥梁的合理代表。这些假设是：1）桥梁材料是均匀的和各向同性的，并且具有弹性; 2）由于局部屈曲，任何会员都不会失败; 3）通过提供足够的剪切连接，在混凝土甲板和钢梁顶部之间存在完整的复合作用; 和4）为了简化分析，桥面上的路缘和栏杆的作用被忽略。

4. 融合研究

作为数值分析的一部分，对弯曲桥梁模型进行收敛研究，以找出合适的有限元网格尺寸，并确定适当的支撑间距，以防止由于局部和全局屈曲引起的任何不希望的过早失效。 因此，提出了有限元模型对网格尺寸和支撑结构的敏感性。

对于具有曲率比为1.2的60 m跨度的复合曲面桥，尝试了从3000 mm到150 mm不同的元件尺寸（图2），并考虑到六通道载流量，以观察元件尺寸对精度的影响模型并找出收敛点。在进行有限元分析时，将纵横比保持在接近于一个的范围是非常重要的，同时改变元素的大小以获得最准确的结果。

从网格尺寸收敛研究中获得的结果如图1所示。观察到，由于元件尺寸从3000mm减小到250mm，当在模型中使用尺寸为250mm的元件时，相应的变形会收敛。当元件尺寸减小到低于250 mm的值时，设计没有进一步的显着变化。此外，对于小于250mm的元件尺寸，元件和节点的数量可能过大，并降低了模型的效率。例如，对于元件尺寸为500 mm，250 mm和150 mm的型号，元件数量分别为9891,55,355和220,071。

混凝土桥面

网梁（W1）

光圈

顶部法兰和支撑模型为梁元件

壳单元

图3. 箱梁

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[141064]，资料为PDF文档或Word文档，PDF文档可免费转换为Word