斜交空心板梁桥静动力响应分析模型与影响参数分析毕业论文
2020-03-16 13:52:02
摘 要
自从上个世纪80年代以来,提高道路交通网络的通行能力,是为了改善道路的线形,斜交桥已被广泛的应用于城市立体交通枢纽和高等级公路之中。因斜交空心板梁桥具有建筑高度小,施工方便等特点使其成为了斜交侨之中十分重要的一部分。斜交空心板梁桥发展时间较短,受力特性也较为复杂,而对它的研究相对较少,已有的设计方法的理论依据相比不足,使得目前的一些斜交空心板梁桥出现了一些令人意想不到的问题。故此,对其的受力特性和影响参数的研究分析具有比较重要的理论价值和现实意义。
本文对斜交空心板梁桥的发展现状进行了详细的综合叙述,并以此为出发点,确定了本文的研究内容,详细介绍了单梁模型及梁格模型的理论方面内容,并以16m空心板为例,应用Midas civil分别建立0°、10°、20°、30°、40°的梁格模型进行不同角度间的不同模型数据比较以此进行动力特性分析,以及在在汽车荷载作用下进行内力分析,得出横向分布系数,结合梁格理论对斜交空心板梁桥的静动力响应模型分析与影响参数分析进行了以下研究,并得出一些对桥梁工程设计有益的结论。
关键词:斜交空心板梁桥、梁格法、MIDAS/CIVIL、横向分布系数。
Abstract
Since the 1980s, in order to improve the road alignment and improve the traffic capacity of the road traffic network, the skew bridge has been widely used in urban three-dimensional transportation hubs and high-grade highways. Due to the small height of the building and the ease of construction, the oblique hollow slab girder bridge has become a very important part of the skewed overseas Chinese. Oblique hollow slab girder bridges have a shorter development time and are more complex in their stress characteristics. However, there are relatively few studies on it, and there are relatively few theoretical foundations for the existing design methods. As a result, some current skewed hollow slab girder bridges appear. Some unexpected problems. Therefore, the study and analysis of its stress characteristics and influence parameters have more important theoretical and practical significance.
In this paper, a detailed and comprehensive description of the development status of oblique hollow slab girder bridges is given. Taking this as a starting point, the research content of this paper is determined. The theoretical aspects of the single beam model and the lattice model are described in detail, and the 16m hollow is used. For example, using the Midas civil to establish grid models of 0°, 10°, 20°, 30°, and 40°, respectively, to compare the different model data from different angles to analyze the dynamic characteristics, and to analyze the internal forces under the action of the vehicle load. Based on the horizontal distribution coefficient and the beam lattice theory, the following researches were conducted on the static and dynamic response model analysis and influence parameter analysis of the skewed hollow slab girder bridge, and some conclusions on the bridge engineering design were drawn.
Key words: diagonal hollow slab girder bridge lattice method MIDAS CIVIL lateral distribution coefficient.
目录
第一章 绪论 1
1.1研究意义 1
1.2研究现状 1
1.2.1国内的研究现状 1
1.2.2国内研究现状 3
1.3本文的研究内容 4
第二章 模型建立方法与计算模型 6
2.1建模前的准备工作 6
2.1.1工程概况 6
2.1.2截面图导入Midas/Civil 6
2.1.3横向分布系数 8
2.2单梁模型 9
2.2.1单梁模型模型简介 9
2.2.2模型相关参数 9
2.3梁格模型 10
2.3.1梁格模型模型简介 10
2.3.2梁格模型相关参数 12
第三章 动力特性分析 13
3.1空心板单梁模型动力特性 13
3.2空心板梁格模型动力特性 14
3.2.1 0°空心板梁格模型 15
3.2.2 10°空心板梁格模型 16
3.2.3 20°空心板梁格模型 18
3.2.4 30°空心板梁格模型 20
3.2.5 40°空心板梁格模型 21
3.2.6梁格模型特征值汇总表 23
3.3不同模型的比较 24
3.3.1单梁模型与梁格模型数据比较 24
3.3.2梁格模型与梁格模型数据比较 26
第四章 静力特性分析 27
4.1空心板单梁模型静力特性 27
4.2空心板梁格模型静力特性 28
4.3空心板单梁模型与梁格模型静力特性对比 36
第五章 结论与展望 38
5.1结论 38
5.1.1动力响应 38
5.1.2静力响应 38
5.2需要改进之处和进一步研究的建议 38
参考文献 39
致谢 40
第一章 绪论
随着交通运输事业的快速发展,桥梁在城市道路、跨越山河湖泊的领域中发挥着越来越高的作用,尤其是跨海大桥的建立彰显桥梁工程师们挑战天险、技术上不断突破的斗志和决心。在桥梁选择的截面中,空心板梁在中小跨径的城市桥梁道路中发挥愈加凸显的位置,在城市的建设中也是应用广泛。因此,斜空心板梁桥已成为桥梁施工中最重要的桥型之一。而在梁桥中,斜交桥是一种特殊的结构形式,斜交桥本身不同于正交桥,结构、应力状态和结构设计都比正交桥梁复杂得多。斜交桥在发展初期,往往以简支结构形式出现。在工程中常用的有空心板、T型、箱梁、小箱梁等,然而随着要求的提高,包括跨径、桥面承载能力等等,都给斜交梁桥的存在带来很大的挑战。为了解决这些方面问题,本文以斜交空心板为例,对其展开探讨与研究。
1.1研究意义
多梁斜拉桥和斜梁桥在实际工程中是非常常见的两种斜拉桥。随着城市三维交通和高等级公路发展的脚步进程越发迅猛,斜交桥梁在城市三维交通网络和高等级公路中被广泛的应用。然而,由于斜空心板梁桥结构简单、结构轻巧,其静动力响应一直没有人研究过。这将给斜交空心板梁桥的使用带来更多的疏漏和危害。因此,系统地建立了该类桥梁的静动力响应模型。因此对该种桥型的静动力响应模型进行系统的研究是具有理论及工程实际意义的。
1.2研究现状
根据现今所查阅的资料,国内对斜交空心板梁桥的研究很少,而对斜梁桥的设计理论及相关研究相比较多,因此本文借鉴一下,大致有以下对斜梁桥的研究的几种方法:
(1)实验方法
关于斜桥的试验,可以追溯到1948年的Newmark等人,他们建立了单跨简支斜拉桥,比例为1:4,受条件限制,并未有较好的结果。而在之后的1977到1980年间,做了比例为1:2.82的斜交角度为45度箱梁,历经4年研究,得出了重要结论。跨中最大弯矩和支点的负弯矩,与同等的正桥、弯桥有所减小。 (2)数值方法
早期应用到斜交桥结构分析的数值方法是差分法。随着有限元法的提出以及之后计算机技术的突飞猛进,对桥梁结构的研究已经可以通过结构电算来实现。当有限元法和计算机都用于对斜梁桥结构的分析上后,一系列桥梁方向的有限元软件应运而生,其中较为热门的有MIDAS, SAP,,ANSYS以及桥梁博士等,然而这个领域上仅考虑了斜梁桥,而未对斜交空心板梁有过多的分析研究。
而就实际的工程上来说,斜桥的适用领域往往广于弯桥和正桥,另外对于中小跨度桥梁而言,斜桥也是很有竞争力的选择,这种需求随着交通网络的完善而空前膨胀。
(3)修正法
修正法是从荷载的横向分布着手,但是大多都采用正桥的设计思路。当我们在进行内力的计算的时候,首先进行正桥计算,在计算出正桥的结果之后,通过相关的修正法进行修正转化为斜桥的横向分布系数,然而这一方法很有局限性,且未对扭矩对结构的影响有所考虑。
可见,在当前的研究现状下,此次毕业论文关于空心板的研究非常有必要。、
1.3本文的研究内容
在有限元理论的基础上,使用计算机软件的强大计算功能对斜桥的受力情况进行仿真模拟已经成为了分析斜桥的一种常用方法。关于这一方面的研究文献也较为多见,大多数的研究着重于研究斜梁桥和整体式斜板桥的受力特点。本文以16m空心板为例,利用分析软件Midas civil建立在不同角度(0º、10º、20º、30º、40º)下斜交梁桥的模型,运算得出不同模型的数据进行比较,通过对在不同角度(0º、10º、20º、30º、40º)的情况下的汽车荷载作用下的内力计算分析,分析斜交空心板梁桥的动力特性,得出计算结果。论文的主要研究内容如下所示:
(1)采用Midas civil建立各种角度(0º、10º、20º、30º、40º)下16m空心板的空间模型,分析整个模型中各种关键位置量值的内力影响面。分析各种内力量值(剪力、弯矩)在桥面的分布规律。对斜交空心板梁桥的动力作用响应模型进行分析。
(2)计算较大宽度的弯梁桥、斜梁桥时、荷载横向分布这种近似于的处理办法就不打适用于计算多格式箱梁桥的内力。本文通过分别计算不同角度情况下斜交空心板梁桥桥面的弯矩和剪力的二维影响面,进行影响参数分析。
(3)在Midas civil软件的运算功能得出内力计算结果,建立图像模型,进行内力分析。
第二章 模型建立方法与计算模型
为了对此次斜交空心板梁桥的静动力响应分析,通过调整相应参数对模型的计算结果的影响情况,本次设计以梁桥计算模型中常用的两种分析方式,即单梁模型和梁格模型。模型的建立通过桥梁建模过程中常用的有限元分析软件Midas/Civil实现。静力响应以对梁体施加的汽车荷载作为荷载效应组合,分析梁体在此荷载工况下弯矩、剪力的情况。而动力响应则是考察梁体自身的重量,将荷载转化为质量,运用结构动力学的相应知识,研究模型在前五阶模态下的动力响应,并记录各个模态下的频率。在此过程中,寻求对斜交空心板梁桥静动力响应产生影响的相关参数,调整参数的取值,得到不同的数据,并得到参数分析的结论。
2.1建模前的准备工作
在建立模型之前,需要首先对Midas/Civil的建模有整体性的把握。作为桥梁设计师常用的有限元软件,它集众多强大的建模功能于一身,在建模的过程中,将梁体等效分为众多节点和单元,让梁体的受力情况变为这些节点、单元共同承载,并将超静定结构的计算问题利用软件强大的计算能力实现,可以说大大方便了桥梁设计者的时间,甚至对我们这些有限单元法知之甚少的初入门者带来了福音。
2.1.1工程概况
该梁标准跨径为16m,计算跨径为15.56m。采用预应力空心板结构体系。全桥采用预应力钢筋混凝土材料,梁横面图见图2.1,共24块板。为了研究方便,此次建模仅选择单幅桥面,即12块空心板,梁长为12.24m。
 图2.1 梁横断面图
图2.1 梁横断面图
2.1.2截面图导入Midas/Civil
通过AutoCAD绘图软件,将空心板中板及边板截面图绘制出来,并保存为dxf格式,见图2.2。
其中边板宽101.5cm,高为70cm,中板宽为101cm,高为70cm,截面图如下。然后用Midas/Civil中自带的截面特性编辑器,导入dxf截面,划分网格并导出截面文件,命名为16m中板截面.sec和16m边板截面.sec。截面特性见下图2.3。并记录16m中板截面特性,抗弯惯性矩I和抗扭惯性矩IT,分别为:抗弯惯性矩I=2225759cm4,抗扭惯性矩IT=4019780cm4。
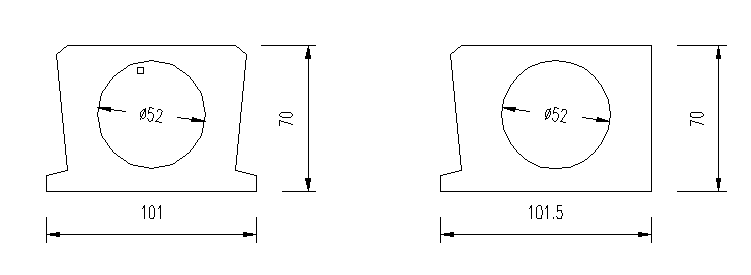
图2.2 中板及边板截面图
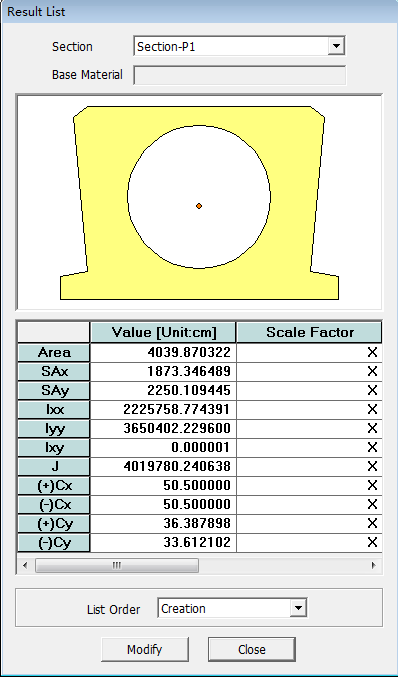
图2.3 midas中板截面特性
2.1.3横向分布系数
之所以将横向分布系数放在建模前的准备工作里,这得益于横向分布系数在桥梁设计中的重要地位。在本科的桥梁工程学习过程中,对简支梁桥的设计计算之前,便对荷载横向分布系数的计算进行了细致的讲解。活载作用在桥面板和众多横梁上时,荷载会分散于主梁间,内力分配十分复杂。为了对主梁间的内力分布有理论上的分配,相关学者们对荷载横向分布计算展开了多方面的探讨,并衍生出众多的方法,如杠杆原理法、铰接板(梁)法、刚性横梁法等等。由于这些方法计算原理不同,各自适用的情况也有差别。在本次毕业设计中,需要建立的模型为空心板梁桥,且各梁体为预制空心板块,采用现浇混凝土连接成一个整体,因此在计算本次模型的横向分布系数,选用的方法为铰接板(梁)法。下面为空心板梁桥的横向分布系数的计算过程:
首先计算空心板的刚度参数γ。由前面记录的抗弯惯性矩I和抗扭惯性矩IT计算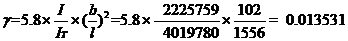 。
。
由计算得到的刚度参数γ查《桥梁工程》附表1 铰接板荷载横向分布影响线竖标表,通过内插累计影响线竖标,得12号梁的横向分布系数。
1号梁 | 2号梁 | 3号梁 | 4号梁 | 5号梁 | 6号梁 | |
跨中_m汽_max | 0.2364 | 0.2362 | 0.2333 | 0.2245 | 0.2093 | 0.2004 |
跨中_m人_max | 0.235 | 0.2 | 0.166 | 0.144 | 0.13 | 0.123 |
7号梁 | 8号梁 | 9号梁 | 10号梁 | 11号梁 | 12号梁 | |
跨中_m汽_max | 0.2004 | 0.2093 | 0.2264 | 0.238 | 0.2433 | 0.2462 |
跨中_m人_max | 0.123 | 0.13 | 0.144 | 0.165 | 0.201 | 0.239 |
表2.4 各梁横向分布系数
2.2单梁模型
2.2.1单梁模型模型简介
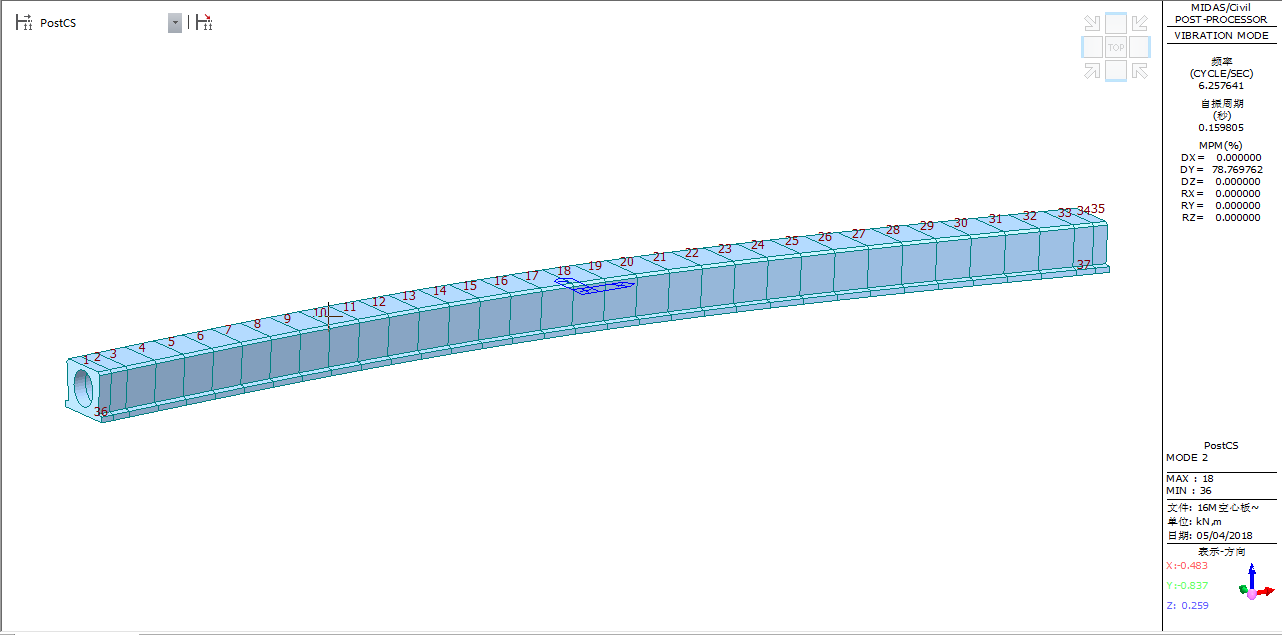
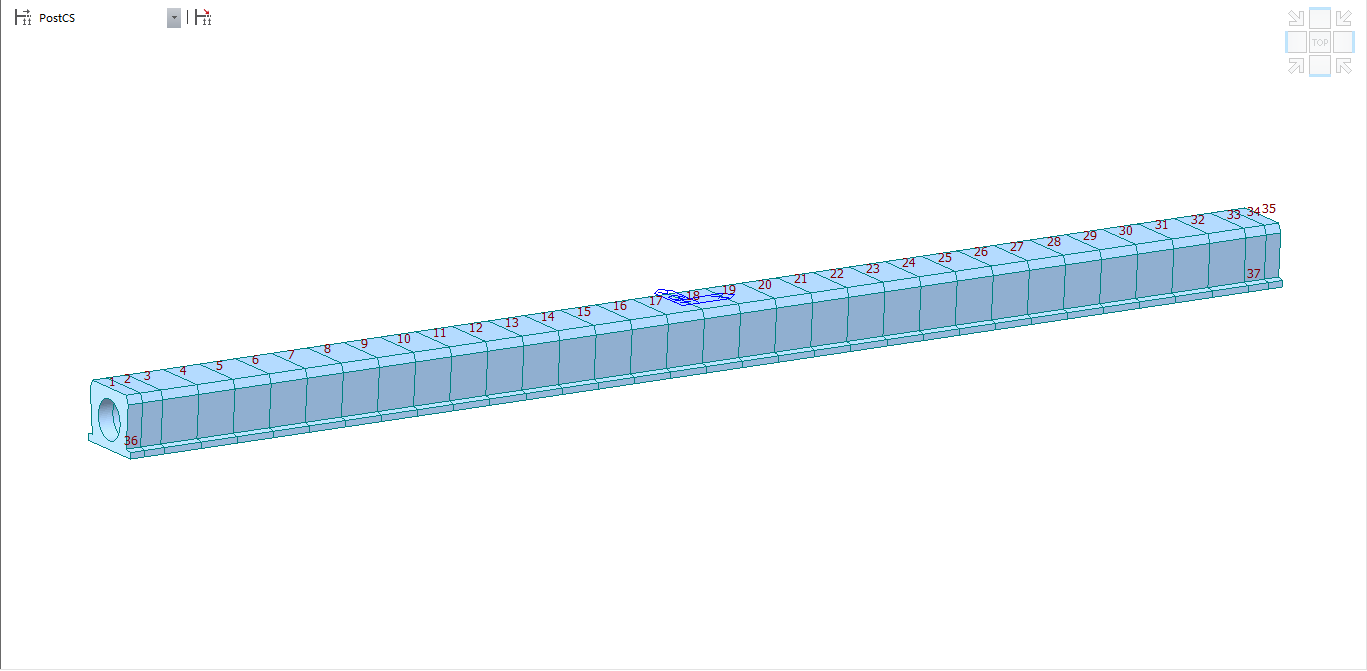
模型为16m跨径单梁模型,该模型由37个节点、34个单元构成。其中节点2与节点34为支座处,与节点36、37采用弹性连接。节点1-10,26-35采用中板端部截面;截面10-35采用中板中部截面,从而构成了单梁模型。在此例中,为方便研究,中板端部截面与中板中部截面采用的截面参数一致。模型的结构离散图如下图所示。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: