GARCH族模型择优及其在股市波动溢出效应研究毕业论文
2020-03-08 10:12:42
摘 要
当今社会迅速传播的信息和流动的资本使股票市场面临巨大的风险,主要体现在股票价格的波动性复杂,过于频繁的市场波动会破坏市场的稳定性。因此,文章着重研究我国沪深两市的波动性特征,了解股市之间的波动溢出效应,对我国监管者及广大投资者具有重要的现实意义。本文选取上海综合指数和深圳成负指数作为研究对象是因为这两个指数能有效反应上海股市和深圳股市价格波动的主要特征,也是投资者投资行为的评价标准和主要参考要素。本文通过Eviews7.2计量分析软件,运用GARCH族模型对上海综指和深圳成指指数收益率序列进行拟合,通过比较不同残差分布假设下的AIC值和SC值得到GED分布下的GARCH族模型是拟合程度最好的模型。然后通过计算VaR值和kupiec检验方法比较GED分布假设下的三种不同GARCH模型得到GARCH-GED模型是度量风险价值的最有效模型。最后对最优模型建模后的残差平方序列进行Granger因果检验分析两个股市的波动溢出效应。通过对股市的波动性和风险能力的评价以及两个股市的相互影响作用研究,对投资者和监管者具有一定指导意义。
关键词:GARCH族模型 GED分布假设 kupiec检验 Granger因果检验
Abstract
In today's society the rapid transmission of information and capital flows to the stock market is facing huge risk, mainly reflected in the volatility of stock prices, too frequent market volatility can destroy the stability of the market. Therefore, it is of great practical significance for China's regulators and investors to study the volatility characteristics of Shanghai and shenzhen stock markets and to understand the linkage effect between stock markets. This article selects the Shanghai composite index and shenzhen into negative exponential as the research object is because the two index can effectively response the Shanghai stock market and shenzhen stock market fluctuations in the price of the main profile, also is the main reference index of investors investment decision and evaluation standard. In this paper, by using Eviews7.2 econometric analysis software on the Shanghai composite index and shenzhen component index index yield sequence for the family of GARCH model fitting, by comparing the different residual distribution under the assumption of AIC and SC get GED distribution under the GARCH model is the most effective fitting model. Then, by comparing the three different GARCH models under the GED distribution hypothesis with the VaR value and kuimport test methods, it was concluded that the garch-ged model was the most effective model to measure the risk value. Finally, the residual square sequence of residual error after modeling the optimal model of Granger causality test is used to analyze the volatility spillover effect of two stock markets. Through the evaluation of the volatility and risk capability of the stock market and the study of the interaction between the two stock markets, it has certain guiding significance for investors and regulators.
Key words: GARCH family model GED distribution hypothesis kupublications test Granger causality tes
目录
1绪论 1
1.1研究背景和意义 1
1.1.1研究背景 1
1.1.2研究意义 1
1.2国内外研究现状分析 2
1.2.1国外研究现状 2
1.2.2国内研究现状 3
1.3研究方法与框架结构 3
1.3.1研究方法 3
1.3.2框架结构 4
2先导知识 4
2.1金融市场波动的概念及特征 4
2.1.1金融市场波动概念 4
2.1.2金融市场波动特征 5
2.2波动溢出效应的概念及原因 5
2.2.1波动溢出效应概念 5
2.2.2波动溢出效应产生原因 5
2.3本章小结 5
3 不同分布假设GARCH族模型理论 5
3.1ARMA模型 5
3.2ARCH效应检验 6
3.3ADF检验 6
3.4GARCH模型族 7
3.5不同分布假设下的GARCH族模型 10
3.5.1广义误差(GED)分布 11
3.5.2学生t分布 11
3.5.3不同分布假设下的GARCH族模型 11
4不同分布假设下的GARCH族模型择优及相关理论研究 13
4.1AIC准则 13
4.2SC准则 13
4.3VaR模型检验 14
4.3.1VaR模型检验的基本思想 14
4.3.2Kupiec-失败频率检验法 14
4.4Granger因果检验 14
5.实证分析 15
5.1数据的选取及处理 15
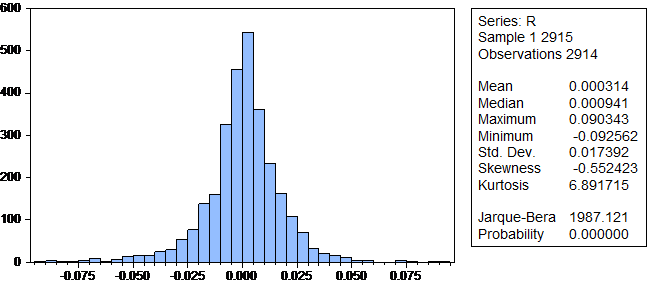
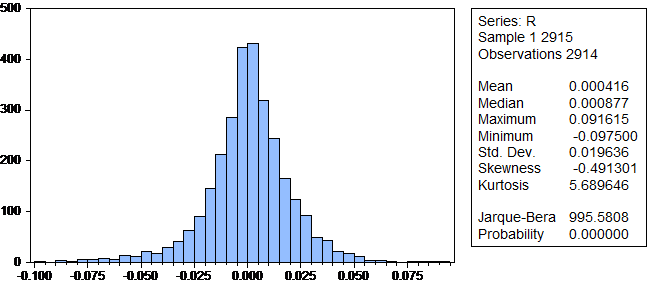
5.2样本数据的描述性统计分析 15
5.3不同残差分布的GARCH族模型比较 22
5.3.1GARCH(1,1)模型的建立与比较 22
5.3.2EGARCH(1,1)模型的建立与比较 25
5.3.3PARCH(1,1)模型的建立与比较 26
5.4GED分布假设下GAECH类模型的应用与检验 28
5.4.1GED分布假设下的GARCH类模型的VaR计算 28
5.4.2GED分布假设下GARCH类模型的检验 30
5.5我国股市波动溢出效应分析 31
5.5.1数据样本的选择 32
5.5.2平稳性检验 32
5.5.3Granger因果检验 33
6结论与展望 33
6.1总结 33
6.2展望 34
参考文献 35
1绪论
1.1研究背景和意义
1.1.1研究背景
上海证券市场和深圳证券市场分别于1990年12月19日和1991年7月3日成立,发展迅速,深刻影响我国实体经济的发展。但是由于信息披露制度、市场交易制度、市场监管制度和惩处等制度的不完善,股票市场作为一个新兴市场,表现出以下特点:1、同期周转率和市盈率远远高于其他资本市场,高周转率反应股票市场活跃度高的同时也反映了市场的投机性,高市盈率反映上市公司高成长性的同时也反映了股市存在泡沫的非理智的投资行为。2、价格波动幅度大、频率高。我国股市经历过多个大涨大跌的局面,在全球范围内其波动特征也十分明显。3、受政策影响大。监管机构的政策变化对市场波动性具有重要影响。股市的这些特点易诱发金融风险,造成资源不合理配置、信用危机、金融不稳定等严重问题,从而影响实体经济的发展。经济学家开始在股票市场的波动性领域不断研究,发现我国股市收益率时间序列数据具有“尖峰厚尾、波动集聚”的特征,若使用传统的假设方差保持不变的计量方法进行拟合分析会误差比较大,不能很好的描述其特征。为了提高模型的拟合度和可预测性,学者们对传统的计量模型进一步研究,美国经济学家Engle首先提出了ARCH模型(自回归条件异方差模型),之后为扩大ARCH模型的使用范围,Bollerslev提出了广义条件异方差自回归模型(GARCH模型),经验证该模型能更有效描述时间序列数据的波动性,但是正太分布假设下的GARCH模型无法刻画时间序列的尖峰厚尾现象,所以学者们进行了更深入的研究,对于提出了多种GARCH模型的不同残差分布假设,包括简单的Bollerslev的t分布假设和Nelson的GED分布假设,再扩展到复杂的拉普拉斯分布和Nolan的稳定分布。在不同残差分布假设下,GARCH族模型的尾部拟合效果是不同的,因此模型拟合性和预测能力也各有优缺点,文章选取了适用范围最广的GARCH族模型的三种残差假设分布,在残差分布下选择最合适的GARCH族模型,探究哪种残差分布能够更有效地描述我国股市的波动性并具有良好的表现。
1.1.2研究意义
股票市场可以通过波动性特征表现出来,因此通过研究波动率来预测可能遇到的风险程度。因此关于波动率的度量一直是金融领域关注的问题,有利于分析当前的经济形势和预测未来的走势,对指导投资者行为具有重要意义。一般我们采用方差和标准差来度量波动率,但对于金融时间序列数据,波动率是随着时间变化的,因此学者们开始探究描述金融中波动率的方法。由最开始的ARCH模型(自回归条件异方差模型),随后出现的GARCH模型(推广的自回归条件异方差),之后提出的GARCH-M模型、EGARCH模型、TGARCH模型也遵循广义自回归条件异方差性。因此,文章重点关注上海综指和深圳成指在2005年1月1日至2016年12月30日的日收益率情况,对其收益率的波动性和两市的联动性运用GARCH族模型进行分析研究,不仅可以更好地理解股市波动性,还可以预测未来股市变化趋势。由于对经济的影响越来越大,金融经济学家开始深入研究股市波动特征。本文利用GARCH模型族对上海综指和深圳成指指数收益率进行波动性研究,不但丰富了我国波动率研究中的实证分析部分,而且具有一定的现实意义。波动率在反映股票市场价格变化的同时也是度量市场效率的标准,投资者和监管者在投资和制定政策时以波动性为重点。对于股票投资者而言,熟悉股票市场波动性规律能指导其投资行为,理性投资、科学决策,避免巨额亏损。对于股票市场监管者而言,波动性的研究帮助其制定科学合理的监管制度,有效识别金融风险并加以应对,避免金融危机。对于股市是经济发展的晴雨表,了解股市波动性规律有利于政府制定紧缩或宽松的政策调节宏观经济运行。股价波动性规律还能帮助上市公司制定经营战略,有效应对行业竞争者。有效的市场波动性对市场投资者和国民经济都有重要影响,对投资者在股市中的行为和监管具有重大的指导意义。
1.2国内外研究现状分析
1.2.1国外研究现状
西方学者在金融市场波动性领域取得了显著的成果。最开始Mdanlebrot(1963)提出股票市场的波动具有集聚性,即小的波动伴随着小波动,大波动伴随着大波动。Box和Jenkins建立的ARMA模型,为研究时间序列模型的研究奠定了基础。美国经济学家Engle于1982年构建了自回归条件异方差模型(ARCH模型),被广泛用于股票、期货、货币、外汇等市场波动性的研究。1986年,为解决ARCH模型存在高阶滞后项问题,Bollersev发展了广义ARCH模型(GARCH模型)。此后,Engle、Liken、Robins通过在均值方程中加入条件方差得到GARCH-M模型,。后来,Black发现了波动对价格上升或下降的反应是非对称性的,被称为股价波动的杠杆,Glosten、Jagannathanamp;Runkle、Zakoian和Nelson提出了GJR、TARCH和EGARCH三个非对称模型。随着研究的深入,学者们发现在正态分布的假设下对时间序列进行建模拟合程度不高,预测能力也有所下降,学者们开始考虑收益率数据模型中的尖峰现象,用具有粗尾特征的分布来描述数据特征。Bollerslev等人发现了学生t分布,Nelson等人则提出了另一种假设分布——GED分布来研究时间序列数据的厚尾特征,而Hensan、Lambert改进的偏斜学生t分布在描述厚尾特征基础上还描述模型的偏斜特性。之后,Grange和Ding提出了拉普拉斯分布及Panorska和Mittnik提出的平稳帕累托分布,这些分布也被用于研究时间序列数据中。
1.2.2国内研究现状
国内学者对金融时间序列收益率波动的研究也在持续增长。邹建军和张宗益基于GARCH模型的VaR模型研究了我国股市收益率数据的尖峰厚尾性[1]。赵慧和石先进基于T-GARCH模型分析了中国股市的利率和国外股价波动情况,已经发现利率、汇率和国外市场对我国股市的波动具有重要影响[2]。陈科研究GARCH-M在我国资本市场的应用,得出GARCH-M模型不适用于描述基金市场价格变化而GARCH(1,1)模型能拟合基金市场的收益率更好[3]。陈盛双和李化想研究2003到2007年上证综合指数,结果表明上海证券市场股价在这段时间内具有尖峰厚尾性、异方差性和非对称性。刘玄和冯彩研究上证综合指数2005年6月到2008年8月的日收盘价,并将数据拟合成GARCH模型和EGARCH模型,发现在此时间内具有显著的不对称性[5]。王汉生(2010)研究了准极大似然法对不同分布假设下的模型进行参数估计,比较模型的拟合程度优劣。薛涵予(2011)选取深圳股市数据作为研究对象,采取三种不同类型GARCH模型:参数、半参数和非参数来拟合数据,通过比较结果发现半参数模型的结果最好,参数GARCH模型的预测能力最差[10]。王艺霖和周渊(2012)研究多元GARCH模型,将交易量加入模型变量中以获得VGARCH模型,拟合上海股票市场数据,结果表明VGARCH模型的预测能力较强,并且得到股市的波动性反映股市中信息的传导效应大于交易量的模型参数。
1.3研究方法与框架结构
1.3.1研究方法
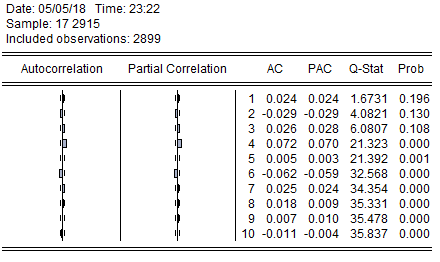
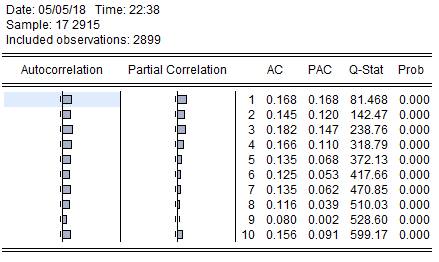
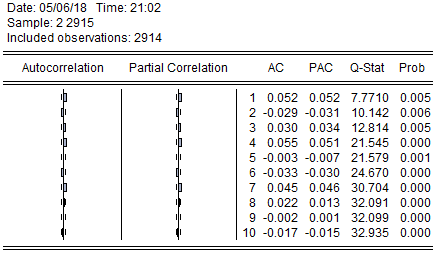
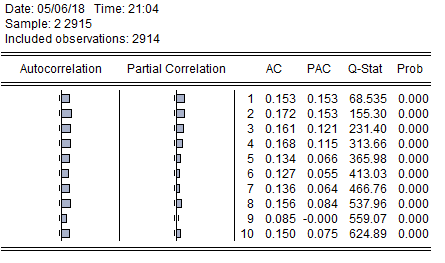
学习国内外相关文献后,查找到本文需要的GARCH族模型、VaR研究方法、Granger因果模型和相关研究模型。运用实证分析对各类模型进行实证分析,找到拟合我国股市收益率指数和度量风险价值的合适模型,采用定量和定性的方法进行理论和实证分析结合。在理论方面采用对比分析和定性、定量推导方法。实证方面运用Eviews和Excel软件对数据进行分析,主要用ADF单位根检验、正态分布检验、自相关检验、ARCH-LM检验对数据进行初步分析,然后用EVIEWS软件对GARCH族模型进行数据建模,通过比较AIC和SC的值,选出拟合程度最高的分布假设下的GARCH族模型,然后运用Var模型和Kupiec失败频率测试选出最优的模型,最后利用最优模型得到的残差平方对上海综指和深圳成指市场进行Granger因果检验探究两市的相互作用能力,即波动溢出效应。
1.3.2框架结构
全文共分为六部分,具体安排为:
第一部分为绪论。首先阐述了本课题的研究背景,选题意义,并对国内外学者对研究课题的研究过程和成果进行了梳理。
第二部分为金融市场基础知识陈述,介绍了金融市场波动性定义及相关特性,波动溢出效应产生的内在原因。
第三部分为GARCH族模型理论阐述。这部分详细介绍了时间序列数据的基础分析方法,有单位根检验、自相关检验和ARCH-LM检验等,然后介绍了GARCH族模型及相关理论基础,最后介绍了GARCH族模型在三种常见分布假设下的具体表示方法。
第四部分首先介绍了AIC指标和AC指标,用来衡量不同分布假设下的GARCH族模型拟合程度优劣,然后基于GARCH族模型构建Var模型,运用Kupiec失败频率检验法比较不同GARCH族模型预测风险价值的准确度,最后介绍Granger因果检验研究两市的波动溢出效应。
第五部分为实证分析部分,这部分选取上证综指和深圳成指日对数收益率序列为研究对象,通过比较不同分布假设的GARCH族模型,然后选出最优分布假设的GARCH族模型进行Var模型拟合和Kupiec检验,并选出最适合模型的残差平方进行Granger因果检验。
第六部分为总结,对本文研究的总结及不足之处进行详细的总结归纳。
2先导知识
2.1金融市场波动的概念及特征
波动性是金融市场的主要特征,波动溢出现象是波动性的主要表现,本文旨在对两市指数的波动性进行实证研究以分析波动性的变化规律,在构建模型之前我们要对波动性的原因和特征详细描述以理解波动性变化规律。
2.1.1金融市场波动概念
金融市场波动性指金融市场的某个变量围绕均值水平随时间变化变动的现象。金融市场的投资活动受各种因素影响,某个因素变化则会引起市场波动性,因此波动性是复杂且时刻变化的。因此,研究市场波动性对于金融风险研究、资产分配及资产定价有重要意义,因此许多国内外学者对波动性进行模型研究和改进。
2.1.2金融市场波动特征
各种因素影响的共同作用是波动率具有复杂的变化特征,分别为为:(1)集聚性。投资者对某一事件的变化会影响波动性,所以往往大的波动后会伴随大的波动,而小的波动会伴随较小的波动。(2)持续性和长记忆性。持续性指金融市场现在的波动会对之后的波动产生连续不断的影响。长记忆性指变量的自相关性非常显著并会保持一段长时间。根据这两个特征可以利用过去信息预测未来。(3)尖峰厚尾性。金融市场的波动并不服从正态分布,而是呈现尖峰厚尾特征,表现为在均值附近的值更多且具有拖尾现象。
2.2波动溢出效应的概念及原因
2.2.1波动溢出效应概念
由于大数据和电子信息技术发展,信息传递成本越来越低,所以各个金融市场连接更加紧密,一个市场的波动不仅受自身的影响,还受到其他市场的影响,这种现象称为波动溢出效应。
2.2.2波动溢出效应产生原因
波动溢出效应产生的原因基于三个原因,首先是金融管制放松,政府对金融活动的方位和进入壁垒放宽,使信息在各个资本市场流动,加强了市场的联动性。其次是信息溢出,也是波动联动性的根本原因,信息的快速传播是金融产品价格波动不断变化,而价格的变化可以反应市场的有效信息。最后是投资者由于羊群效应产生的投资行为会影响价格的波动性和市场的稳定性。
2.3本章小结
本章介绍了金融市场波动性和波动溢出效应的相关理论知识,阐述了波动产生的内在原因和下文进行实证研究的现实意义,为进行金融数据模型拟合奠定理论基础。
3 不同分布假设GARCH族模型理论
3.1ARMA模型
ARMA模型有三种表现形式,包括自回归模型(AR:Auto-regressive),移动平均模型(MA:Moving-Average)和混合模型(ARMA:Auto-regressive Moving-Average)。
(1)自回归模型AR(p):如果存在时间序列数据{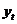 }且
}且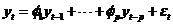 ,
,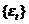 满足
满足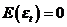 ,
,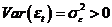 ,则{
,则{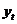 }遵循p阶自回归模型,或称
}遵循p阶自回归模型,或称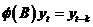 。
。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: