摘 要

本文主要研究了大整数因子分解的各种算法及其在RSA模型中的应用及其比较，还有大整数因子分解在RSA中的应用，大整数因子分解最优算法的数学理论及扩展

研究结果表明： ECC算法比较优化实用性比较高

关键词：算法，RSA,ECC。

Abstract

This paper mainly studies various algorithms of large integer factor decomposition and their applications and comparisons in RSA model, as well as the application of large integer factor decomposition in RSA, the mathematical theory and extension of the optimal algorithm of large integer factor decomposition.

The results show that ECC algorithm is more practical than optimization.

Key words: algorithm, RSA, ECC.

目录

第1章 绪论 4

第2章 大整数因子分解常用算法及其比较 7

2.1试除法 7

2.2 费马因子分解 7

2.3 pollard rho 8

2.4 pollard p-1 9

2.5椭圆曲线算法 9

2.6 基于组合同余的因子分解算法… … …………………………………………10

2.7 数域筛法………………………………………………………………………11

第3章 大整数因子分解在RSA中的应用…………………………………………………………15

第4章 大整数因子分解最优算法的数学理论及扩展……………………………………18

参考文献 25

致谢 27

附录 28

第一章 绪论

为了鼓励更多的人加入研究大数分解问题的行列，跟踪整 数分解研究进展，早在 1991 年，RSA Laboratories发起了RSA模数分解挑战赛，它们发布了十进制位数从100 ～ 617 位的 54 个 ＲSA 模数，并称任何组织和个人，不管使用什么样的技术手

段，只要分解了其中的任意一个数即可获取他们的高额奖金。 20 年过去了，有 18 个数获得了分解结果，它们分别是 RSA100 ～ RSA-704 的最小的17 个数以及 ＲSA-768。表 1 是 2000 年 以来 RSA 模数分解情况。表 1 RSA 模数分解情况

目前，大数分解已经完全脱离了暴力试除的时代，研究者 们已经提出了 ρ 方法、 P －1 法、椭圆曲线算法、随机平方法、二 次筛法和数域筛法等大数分解技术。在过去的十多年里，为了 保证安全，ＲSA 密钥的二进制长度由512 位增长到了现在的 1024，并且安全性级别高的要求使用 2048 位。 近些年来，对于该问题的研究主要集中在纯理论上，对实 现技术的研究则相对较少。宏观来看，具体可以归纳为以下几 个方面:

a)算法创新与改进。迄今为止，大数因子分解问题既没 有被证明多项式时间可解，同时也未证明 ＲSA 的破译与模数 分解是否同等困难。目前已经出现了十几种大整数分解的算 法，具有代表性的大数分解算法有试除法、二次筛法(quadratic sieve，QS)、椭圆曲线算法(elliptic curve method，ECM)以及 数域筛法(number field sieve，NFS);在过去两年也有新的算法 出现如文献。当然，前者是基于量子计算机，后者时 间复杂度未知，新算法的出现并没有取代已经熟知的算法。下 文将一一介绍当前流行的、典型的整数算法。此外，关于对当 前流行的算法的改进也是该问题的研究热点之一，研究最热的 当属对数域筛法的改进，如文献［13］，这只是对数域筛法多项 式的改进。数域筛法目前最高效，但复杂又难以控制、选择合 适的参数对性能影响很大，对它的研究与改进自然是最热的。 具体的改进将在3． 3 节介绍。 b)分布式计算与并行处理。大整数的分解经过几个世纪 的研究，人们还没有发现多项式可解的算法。近些年来，随着 分布式处理技术的发展，人们开始希望从并行处理的角度加快 大规模模数的分解，文献等可以归纳为这一类。近 年来，不管是采用网格技术还是 Hadoop，主要还是将二次筛法 部署到分布式平台上，数域筛法颇为复杂，这也是没有选择数 域筛法的原因。二次筛法和数域筛法的介绍详见后文。 c)基于硬件平台的设计与实现。由摩尔定律可知，硬件 技术发展迅速，新的硬件平台层出不穷，将现有的整数分解算 法移植到硬件平台从而加速整数分解，也是主要的研究点之 一。文献是对椭圆曲线算法的硬件化;文献则 是用硬件来加速二次筛法;文献结合 Xilinx FPGA 实现了 数域筛法，设计了专用整数分解设备，并且第一次给出了用硬 件实现整数分解的实现和实验数据，成功分解了 RSA-128。硬件平台的多样化给这一问题带来了很多研究空间，当前椭圆曲 线(ECM)硬件化的研究比二次筛法或者数域筛法都更热，这 主要是因为 ECM 的算子更能适应流水线结构。可以看出，如上展开的三个方面的研究主要是围绕以后的 椭圆曲线算法、二次筛法和数域筛法三者进行，其中数域筛法 被认为是目前最好的算法。在现有的十几种大数分解算法，根 据能被分解整数是否具备特殊的形式，可将它们分为专用算法 和通用算法;根据算法性能是否依赖于被分解数的光滑性，可 将它们分为基于光滑性的算法和基于组合同余的算法两类。 本文将按照后者分类方法展开对各个算法的介绍。

信息安全是一门涉及计算机技术 、网络技术 、信息论 、密码学 、应用数学 、通信 技术 、法律和管理技术等的综合性学科 。 其中 ，密码理论占有重要的位置 ，是信息 安全的核心和基石 ，甚至可以说 ，离开了密码学 ，信息安全就无从谈起 ，可见密码学 在信息安全领域的重要地位和作用 。 密码学（cryptology）包括两个分支 ：密码编码学（cryptography）和密码分析学 （cryptanalysis） 。 密码编码学是对信息进行编码实现信息隐藏的一门学科 ，主要 研究实现信息保密和认证的方法与技术 。 密码分析学是研究如何破译密码的一门 学科 ，主要目的是研究密文的破译和消息的伪造 。 历史上 ，密码学主要研究加密机制的设计和分析 ，为信息隐藏和保密通信提供 方法和手段 。 中国古代秘密通信的手段是将信息隐藏在文本中 ，据枟武经总要枠记 载 ，北宋前期 ，在作战中曾用一首五言诗的 ４０ 个汉字 ，分别代表 ４０ 种情况或要求。 １８７１ 年 ，由上海大北水线电报公司选用 ６８９９ 个汉字 ，代以四码数字 ，成为中国最 早的商用明码本 ，同时设计了由明码本改编为密本及进行加乱码的方法 ，在此基础上逐步发展为各种比较复杂的密码 。 在欧洲 ，公元前 ４０５ 年，斯巴达的将领来山得使用了原始的错乱密码；公元前 １ 世纪 古罗马皇帝恺撒曾使用有序的单表代替密码 ；之后逐步发展为密本 、多表代替等多种密码体制 。 在公钥密码出现以前所用的密码体制的安全性都基于私钥和加密方法的保密 ， 也就是说算法是不公开的。 由于这种密码体制的代价昂贵 ，因此密码学主要应用于 军事 、政府和外交等机要部门。当时密码学几乎是国家安全机制独占的领域。 在传统密码中 ，用于加密的密钥和用于解密的密钥是相同的 ，因此通常使用的加密算法比较简单 、高效 ，密钥简短 ，安全性高。 但是，传送和保管密钥是一个严峻的问题 。 １９７６ 年 ，D iffie 和 H ellm ann 发表了著名的论文枟密码学的新方向 ，提出了公钥密码体制的新思想 ，证明了在发方和收方之间不需要传递密钥的保密通信是可能的 ，它使密码学发生了一场变革 ，在密码学的发展历史上具有里程碑式的重要意义 ，具有传统密码不可取代的优势 。 为了适应计算机通信和电子商务迅速发展的需要密码学的研究领域逐步从消息加密扩展到数字签名 、消息认证 、身份识别 、防否认等新的课题 。 同时密码学不再局限于军事 、政治和外交 ，而扩大到商务 、金融和社会各个领域 ，特别是互联网的出现和发展 ，为人们提供了快速 、高效和廉价的通信 ，大量敏感信息常常要通过互联网进行交换 。由于互联网的开放性 ，任何人都可以接入互联网 ，使得一些人就有可能采用各种非法手段窃取 、假冒 、欺骗 、篡改和破坏各种重要信息 ，甚至进行计算机犯罪 。从某种角度来讲，正是因为存在的种种信息安全问题 ，才催生了信息安全技术的发展 。 事实上，现在网络上应用的保护信息安全的技术，如数据加密技术、数字签名技术 、消息认证与身份识别技术 、防火墙技术以及反病毒技术等都是基于密码学来设计的 ，由此可见 ，现代密码学的应用非常广泛 。 在任何企业 、单位和个人都可以应用密码技术来保护自己的信息 。 在当今高度信息化的社会里 ，信息安全关系到 国家的全局和长远利益 ，各国政府都十分重视密码学的研究和应用 。 美国国家标准局首先制定并于 １９７７ 年向全世界公布了美国数据加密标准 D E S 。 １９９４ 年又公布了美国国家标准技术研究所（N IST ）提出的一个数字签名标 准 。 １９９７ 年 ，美国国家标准技术研究所又在全世界公开征集高级加密标准（A E S ） 活动 ，通过公布 １５ 个候选加密方案进行公开的评论和专家讨论 ，最后从中选出了 一个方案作为 A E S 。 A E S 将成为新的美国数据加密标准和一个供全球免费使用 的数据加密标准 。 最近 ，欧洲委员会的信息社会技术（IST ）规划出资 33 亿欧元支持一项新的欧 洲数字签名 、信息完整性和加密方案（NESSIE）工程 ，目标是推出一套密码标准，包括分组密码 、流密码 、杂凑函数 、消息认证码 、数字签名和公钥密码等 。 所有这些密码标准的研究和公布，将为信息安全提供强大的理论基础和技术支持 。

第二章

1.试除法

1.1基本思想：根据定义，给定一个自然数，先判断它是否是素数。若要计算出所有不大于n的素数，则从2到n，依次判断是否是素数。根据如何判断一个数是否是素数又有以下几种常规方法。

1.2 实现方法

A．常规方法一：为了判断自然数x是否是素数，我们可以从2开始，分别除以不大于x的每个数，如果存在能整除x的数，则x不是素数。该方法的时间复杂度O（n²）。

B：如果n为合数，已知n=X，假设n=xy，如果xgt;，那么必然小于ylt;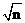。即我们只需要判断到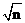即可。该方法的时间复杂度O（n）。

C:欧拉筛法：核心思想就是依次剔除素数的倍数。这里我们很容易就能想到此算法存在的缺点：对于两个素数的公倍数，我们可能会进行多次剔除。核心思想便是对于一个没被筛选过的数来说，它只需要被第一个整除它的素数筛掉就行。该方法的时间复杂度O（n）。

2.费马因子分解：

2.1基本思想： 对于任一个奇数n，n = ab = x²-y²

∵ n = ab = (x y)*(x-y)

    ∴ a = x y, b = x-y

       x = (a b)/2, y = (a-b)/2 (因为n为奇数，a, b必也为奇数，所以(a b)和(a-b)必为偶数，故能被2整除，x, y为整数，x gt; y)

y² = x² – n

∵ x² – n gt;= y² gt;= 0

∴x² gt;= n, x gt;= sqrt(n)

∴我们可以从x = sqrt(n)开始，计算x² – n为完全平方数即可求出x, y，然后求得a, b

2.2利用完全平方数十位和个位数值性质改进费马因式分解算法

完全平方数的最后两个十进制数字（个位和十位）一定是下列数对之一：{00, e1, e4, 25, o6, e9}

结果：用了完全平方数的性质后，将原来需要计算y的开方和比较y²的次数减少了13次（86%），我们知道计算乘法和开方式非常耗费时间的，减少这些次数后可以大大提高算法效率

3.pollard rho分解算法

详解：Pollard_rho算法的大致流程是 先判断当前数是否是素数（Miller_rabin）了，如果是则直接返回。如果不是素数的话，试图找到当前数的一个因子（可以不是质因子）。然后递归对该因子和约去这个因子的另一个因子进行分解。

那么自然的疑问就是，怎么找到当前数n的一个因子？当然不是一个一个慢慢试验，而是一种神奇的想法。其实这个找因子的过程我理解的不是非常透彻，感觉还是有一点儿试的意味，但不是盲目的枚举，而是一种随机化算法。我们假设要找的因子为p，他是随机取一个x1，由x1构造x2，使得｛p可以整除x1-x2 amp;amp; x1-x2不能整除n｝则p=gcd（x1-x2，n），结果可能是1也可能不是1。如果不是1就找寻成功了一个因子，返回因子；如果是1就寻找失败，那么我们就要不断调整x2，具体的办法通常是x2=x2*x2 c（c是自己定的）直到出现x2出现了循环==x1了表示x1选取失败重新选取x1重复上述过程。

因为x1和x2再调整时最终一定会出现循环，形成一个类似希腊字母rho的形状，故因此得名。

Miller_rabin测试算法：Miller-Rabin算法本质上是一种概率算法，存在误判的可能性，但是出错的概率非常小。出错的概率到底是多少，存在严格的理论推导。

1. 费马小定理

假如p是质数，且gcd(a,p)=1，那么 a^(p-1)≡1（mod p）

如果存在alt;p，且a^(p-1) % p != 1，则p肯定不是素数。

1. 有限域上的平方根定理

如果p是一个奇质数且e≥1,则方程

X²≡1（mod p^e）

仅有两个跟x=1或者x=-1，注意到在模p的意义下,x=-1等价于x=p-1，±1也成为1的平凡平方根；

三、Miller-Rabin算法

对于一个大数n，判断n是不是素数的时候，可以先考虑a^（n-1）≡ 1（mod n）

对于n-1，一定可以拆分成2^s d：

a^n-1=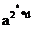 =(((a^d)²)²….)²

可以从x = a^d开始，依次平方s次，每次平方的时候模上n，按照之前的平方根定理，如果模上n的结果为1的话，那么x一定是1，或者是n-1，如果不满足则不是素数，x=x²，再次循环。

每次随机选一个在2-n-1的数字作为a，可以重复测试。

由于mod上的是n，n是一个大数，所以快速幂中的乘法，需要用快速加法来实现。不然就算模上之后再相乘也会溢出。

4.pollard p-1算法

Pollard 在提出了 ρ 方法之后不久，还提出了另一种方 法，称为 P －1 法。假设当 N 有质因子 p，并且 p － 1 是一个平 滑数时，使用这种方法比较有效。 P －1 方法基于费马小定理，该定理是说，对于质数 p 和整 数 a，当 a 与 p 互质时，有 a^p-1≡1(mod p)。根据这一定理，对 于任意整数 k，有 a^{k(p －1)}≡1^k≡1(mod p)。因此对于 p －1 的任 意倍数 M，有 a^M≡1(mod p)，即 p 整除 a^M － 1，又 p 整除 N，因 此 p|gcd(a^M －1， N)，通过求 gcd(a^M －1， N)就有可能得到 N 的 因子。 构造 p －1 的一个倍数 M 很简单，可以给定一个上界 B，将 小于 B 的一些质数或质数的幂乘起来得到 M。这个方法还是 有一定效果的，根据 Brent 的介绍，通过 P － 1 方法找到了 2⁹⁷⁷ －1的一个因子 p32，这是一个 32 位十进制数: p32 =49858990580788843054012690078841 此时 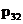－1 =23 ×5 ×13 ×19 ×977 ×1231 ×4643 × 74941 ×1045397 ×11535449 对于给定的上界 B，执行一次 P － 1 算法的时间复杂度为 O(B × log B × log²N)。P － 1 算法能否有效地找到 N 的因子， 取决于 N 的因子 p － 1 是否是平滑的;最坏情况下，(p － 1) /2 是一个质数，此时 P －1 法不会优于试除法。

5.椭圆曲线算法

椭圆曲线方法(elliptic curve method，ECM)是 Lenstra［26］于 1987 年提出来的一种亚指数级复杂度的整数分解方法。这种 方法使用的想法与 P －1 法类似，两个算法成功分解的前提是 它们的群的阶平滑，与 P － 1 方法不同的是，ECM 用随机选择 的椭圆曲线的加法群来取代 P －1 方法中的乘法群 Fp。 ECM 使用了椭圆曲线的群结构，假设 N 是被分解的数，随 机选择一条椭圆曲线 E:y²z = x³ axz² bz³，如果(x， y， z)满足 该方程，并且 c≠0 mod p，则(cx， cy， cz)也满足该方程，因此(x， y， z)和(cx， cy， cz)可以看成是等价的。用(x:y:z)表示包含(x， y， z)一类等价点的等价类。 在这个群 Ea， b中的加法零元 Ο 是(0:1:0)，此时 z =0 mod p，即 z 是 p 的倍数，因此在群 Ea， b中，如果某一步运算得到了加 法零元 Ο = (x， y， z)，那么通过计算 gcd(N， z)就能得到一个大 于 1 的值，这样就可能将 N 分解。 设 P1 = (x1:y1:z1 ) 为椭圆曲线上的一点，nP1 = P1 P1 … P1(共 n 个 P1 相加)，记 Pn = nP1 = (xn:yn:zn)。对于 一个大整数 r 来计算 Pr，一般地， r 是所有小于给定上界 B1 的 质数幂的乘积。群 Ea， b的阶为 g，如果 g 是 B1 幂平滑的，那么 显然有 g|r，而有限群的元素的阶一定是群的阶的因子，因此 Pr 等于加法零元，通过计算 gcd(N， z)可以分解 N。 在 Pollard 的 P －1 方法中，如果第一步处理中算法没有成 功分解 N，即 p －1 不是平滑的，那么可以转入第二步，即允许 P －1有一个质因子大于给定上界。基于同样的思想，Montgomery等人提出可以在 ECM 方法上加第二阶段的处理，改进后 的 ECM 方法允许群 Ea， b的阶 g 有一个大于 B1 但小于 B2 的因 子，这里 0 ＜ B1 ＜ B2 为预先给定的上界。 在 P － 1 方法中，乘法群 Fp 的阶是 p － 1，这种方法只有

P －1平滑时才能分解 N。同样地，ECM 若能成功分解 N，要求 加群的阶也是平滑的。如果某次尝试 ECM 没有成功分解 N， 可以重复随机选择新的椭圆曲线来提高成功率，ECM 的期望 运行时间是 O（ exp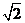（（ O( 1) log p ）^1/2 （loglogp ^1/2 ））其中:p 为 N 的最小素因子。 这个界是所有前面介绍的大整数因子分解算法中最好的 一个界，因此椭圆曲线是所有基于平滑性的分解算法中实际运 行最快的。特别地，当 N 具有小素数因子时，ECM 运行更快。 此外，ECM 还有一个显著的优点，即它占用的内存很少，而后 文要介绍基于组合同余的算法需要大量的存储单元。 Brent ［27，28］使用 ECM 分解了第十和第十一费马数。2012 年 Wagstaff 也使用 ECM 分解出了一个 79 位数的因子，这是 ECM 分解最好最新的记录［29］。