摘 要

零件在加工过程或使用过程中由于摩擦磨损等原因在表面上产生的连续的凹凸不平的微观几何形状即为零件的表面形貌，不仅包括加工纹理、摩擦磨损痕迹，还包括一些特殊的结构，如凹坑、裂纹、划痕等。零件的表面形貌对零件的配合性质、疲劳强度、耐磨性、润滑性等性能有着重大的影响。为了能够充分发挥零件的使用性能，并能及时淘汰使用性能不合格的零件方法之一，是能够方便、快捷地对零件表面形貌的特征参数进行分析与评定。因此本毕业设计基于MATLAB GUI平台，利用小波滤波的相关技术，设计了一套具有交互性、直观性、使用方便的零件表面二维形貌特征的参数评定软件系统。研究工作主要包括：

（1）加载零件表面形貌测量数据，构建了反映零件表面形貌的二维数学模型，通过对该数学模型进行滤波得到二维评定基准，在此基础上获得反映零件表面粗糙度的二维数学模型；利用选取小波基函数的“四项原则”，通过分析常用小波函数的特性，选取了能量守恒的正交小波用于滤波以得到评定基准；采用不同的小波函数对反映零件表面二维形貌特征的数学模型进行分解，根据得到的分解系数重构二维数学模型，根据重构模型与原始模型的误差大小来选取最优小波基函数；根据评定基准面的平均波长和最大波幅的比值来选定合适的小波分解次数。

（2）以IOS25178-2标准为依据，选定九个反映零件表面形貌的参数，并构建三个反映表面磨损量的参数，阐述了这些参数的定义及其表征意义，设计了这十二个参数的算法的具体的编程方法。利用GUI平台，实现了数据加载、特征提取、参数评定、数据储存等功能。

（3）通过向设计的软件中输入假设规律表面的形貌参数和车床、刨床、立铣零件表面形貌的实际测量数据对评定参数的算法进行可行性测试，结果表明参数计算值误差基本在误差允许范围之内，证明了本设计具有一定工程应用价值。

本文的特色：采用了不同于国际标准的小波滤波提取评定基准，并且能够通过软件实现最优小波基函数的自动选择和分解层数的自由选择。

关键词：表面形貌；小波滤波；评定参数；软件设计

Abstract

The continuous uneven microstructure of the part caused by friction and wear during the process or during use is the surface topography of the part, including not only the processing texture, the friction and wear marks, but also some special structures. Such as pits, cracks, scratches, etc. The surface topography of the part has a significant impact on the mating properties, fatigue strength, wear resistance and lubricity of the part. In order to make full use of the performance of the parts and to eliminate the use of one of the unqualified parts in time, it is convenient and quick to analyze and evaluate the characteristic parameters of the surface topography of the parts. Therefore, based on the MATLAB GUI platform, this graduation design uses a related technology of wavelet filtering to design a parameter evaluation software system with interactive, intuitive and easy-to-use two-dimensional features of the surface of the part. The research work mainly includes:

(1) The surface topography measurement data of the part is loaded, and a two-dimensional mathematical model reflecting the surface topography of the part is constructed. The two-dimensional evaluation standard is obtained by filtering the mathematical model, and a two-dimensional mathematical model reflecting the surface roughness of the part is obtained. By using the "four principles" of wavelet basis function, by analyzing the characteristics of common wavelet functions, the energy-conserved orthogonal wavelets are selected for filtering to obtain the evaluation benchmark; different wavelet functions are used to reflect the two-dimensional topography of the surface of the part. The mathematical model is decomposed, and the two-dimensional mathematical model is reconstructed according to the obtained decomposition coefficient. The optimal wavelet basis function is selected according to the error size of the reconstructed model and the original model; the appropriate wavelet decomposition frequency is selected according to the signal-to-noise ratio.

(2) Based on the IOS25178-2 standard, nine parameters reflecting the surface topography of the part were selected, and three parameters reflecting the surface wear amount were constructed. The definition of these parameters and their characterization significance were expounded. The twelve parameters were designed. The specific programming method of the algorithm. Using the GUI platform, data loading, feature extraction, parameter evaluation, data storage and other functions are realized.

(3) The feasibility test of the algorithm for evaluating the parameters is carried out by inputting the shape parameters of the hypothetical regular surface and the actual measurement data of the surface topography of the lathe, planer and end mill parts into the designed software. The results show that the error of the parameter calculation value is basically within the error tolerance range. Within this, it proves that this design has certain engineering application value.

The characteristics of this paper: the wavelet filter extraction evaluation benchmark different from the international standard is adopted, and the automatic selection of the optimal wavelet basis function and the free choice of the decomposition layer number can be realized.

Key Words：Surface topography; wavelet filtering; evaluation parameters; software design

目 录

第1章 绪论 1

1.1 研究目的及意义 1

1.2 表面形貌的评定方法 2

1.2.1 高斯滤波法简介 2

1.2.2 小波滤波法简介 2

1.3 国内外研究现状 3

1.4 本文研究内容 3

第2章 利用小波滤波提取表面特征 5

2.1 小波分析的原理与优势分析 5

2.2 滤波方案的选择 5

2.3 阈值去噪法的原理 6

2.4 最优小波函数的选择 6

2.5 最优分解次数的选择 10

2.6本章小结 10

第3章 机械零件表面形貌参数评定软件的设计 12

3.1 评定系统的总体设计 12

3.2数据文件读取模块的设计 13

3.3 最优小波函数的自动选择模块的设计 14

3.4小波去噪模块的设计 15

3.5小波分解次数选择模块的设计 16

3.6评定参数计算模块的设计 16

3.7数据储存模块的设计 20

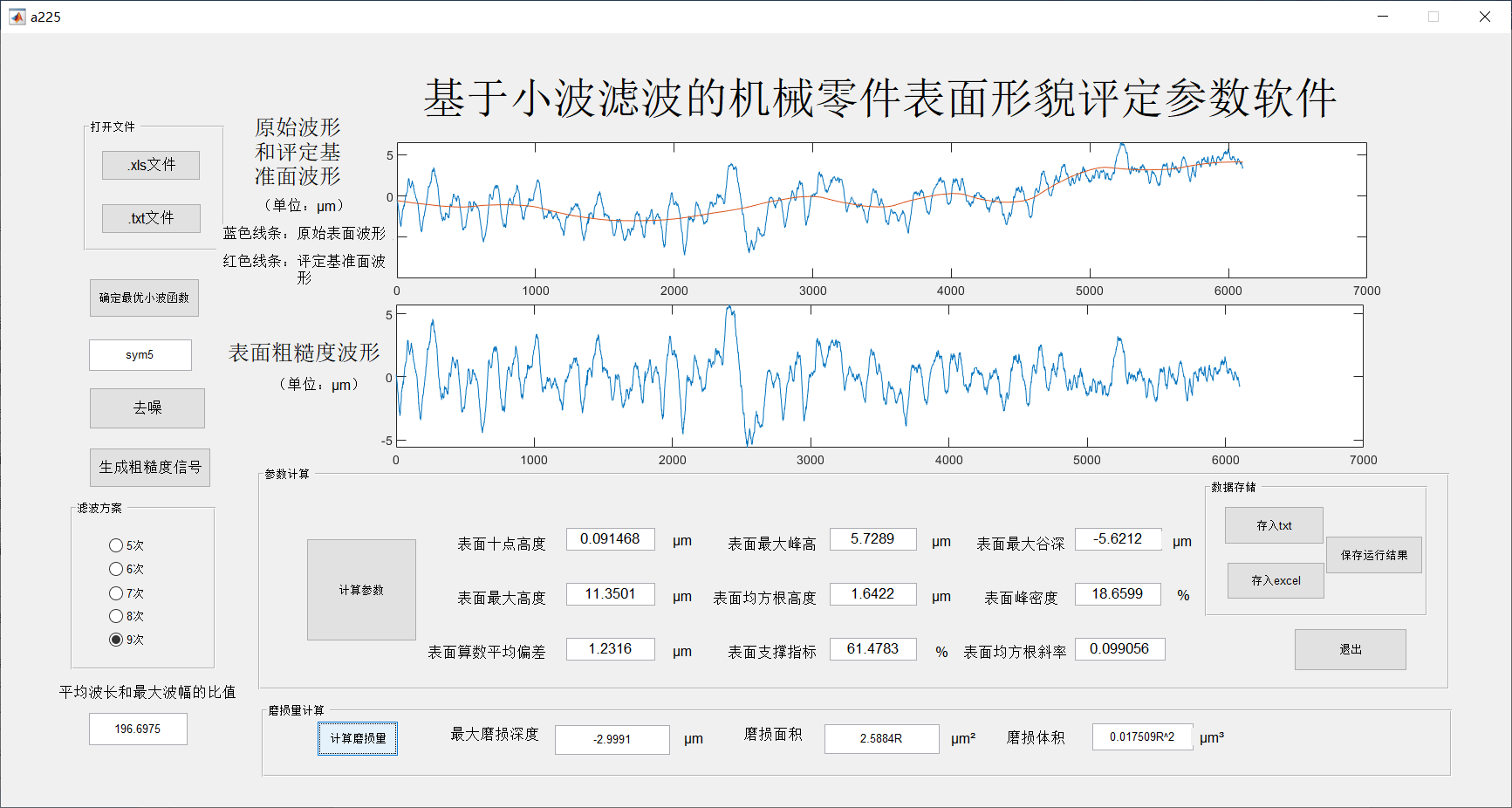
3.8评定软件界面的设计 21

3.9本章小结 22

第4章 表面形貌评定系统的测试 ..23

4.1用于验证的表面形貌的参数 23

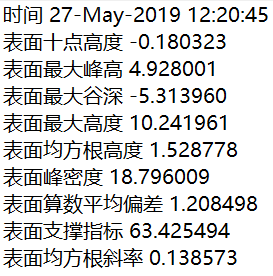
4.2表面形貌评定参数的计算结果以及误差比较 24

4.3表面磨损量算法验证 25

4.4零件表面测量数据的获取 26

4.5评定系统实际测量效果的验证 27

4.6本章总结 28

第5章 总结与展望 30

5.1全文总结 30

5.2工作展望 30

参考文献 32

致谢 33

第1章 绪论

1.1 研究目的及意义

表面形貌（Surface Topography）是指零件表面由于机械加工或者摩擦等原因产生的连续凹凸不平的微观几何形状，除了摩擦痕迹和加工纹理之外，还包括凹坑、凸台、裂纹等特殊的结构形状^[1]。表面形貌分为表面粗糙度、表面波纹度、表面形状误差和表面缺陷四个特征，其中表面缺陷对零件的机械性能而言一般是有害的，应尽量避免。通常，这些表面特征综合影响着零件的使用性能，但由于它们形成的原因、特性以及使用功能的不同，需要对其划分并一一加以分析。

零件表面上间距介于表面粗糙度和表面几何形状误差之间的表面几何不平度被称为表面波纹度，表面波纹度是大于微观但小于宏观的几何误差。表面波纹度本质上是在机械加工过程中由于机床—工件—刀具系统的振动，在零件表面上形成的具有一定周期性的高低起伏。零件表面的机械性能，如零件的接触刚度、结合强度、抗振性和密封性等受到表面波纹度的直接影响。

加工表面上具有的较小间距的峰谷所组成的微观几何形状特征即为称为表面粗糙度，表面粗糙度一般是由所采用的加工方法和其他因素造成的。表面粗糙度对零件的配合性质、耐磨性、抗腐蚀性以及密封性等使用性能有重大影响，也会影响外观质量，是评定零件和产品质量的重要指标。图1.1表示表面形貌的特征及划分：

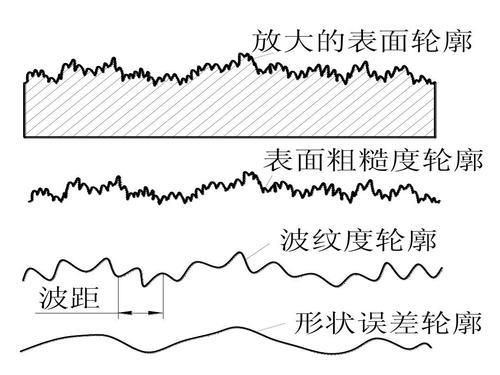
图1.1表面形貌的特征及划分

综上所述，深入分析掌握机械零件的表面形貌特征对该机械零件的应用具有重大意义，因此本毕业设计旨在设计一款零件表面形貌参数的评定软件，来测量零件表面形貌的各种重要参数，达到评估零件机械性能的目的。

1.2 表面形貌的评定方法

零件加工表面形貌特征的无失真分离、提取和分析是表面形貌评定的核心。自从零件表面形貌被作为研究对象以来，研究人员已经提出了很多具有实用价值的表面形貌评定方法，如分型法、小波滤波法、高斯滤波法等。本文将重点介绍研究较多也比较完善的高斯滤波法和小波滤波法。

1.2.1 高斯滤波法简介

高斯滤波是一种广泛用于图像减噪的线性平滑滤波，高斯滤波对图像进行减噪的过程，实际上就是对整幅图像进行加权平均的过程。与传统2RC滤波器相比，高斯滤波是一种零相移的滤波方法，可以通过一次有效滤波提取粗糙度信息，克服了传统滤波器容易发生相位失真的缺陷，因此高斯滤波在形状测量和粗糙度提取方面被广泛应用，在1996 年被国际标准化组织 ISO/TC213 确认为国际标准(ISO11562)。但是使用高斯滤波的前提条件是被处理的波形中峰谷的分布需要服从正态分布，在实际工程应用中，许多工程表面的粗糙度和波纹度都具有特定的频率，不一定严格服从正态分布，而且在零件的表面还会存在一些没有频率的凹坑、槽等表面缺陷，会使滤波的基准发生变形，进而会影响滤波的效果和精确度。

1.2.2 小波滤波法简介

在应用传统的傅里叶变换对含噪声的信号中的信号和噪声进行分离时，只有信号和噪声的频带重叠部分尽可能小，才能保证分离的效果。但是对于频谱重叠的信号，应用传统傅里叶变换进行信号分离的方法就不再适用了。但是基于小波变换的非线性滤波克服了基于傅里叶变换的传统的信号处理的缺点，在这种方法中，即使谱是重叠的，也可以实现信噪分离，但是要求谱的幅度尽可能不同。

小波变换不仅克服了傅里叶变换的缺点，还具有一些能够被称为“数学显微镜”的优秀特性，如在时域和频域方面具有很好的局部化功能，很适于探测正常信号中突变信号的成分。但是由于小波变换所采用的小波基函数有很多种，也就是说，小波函数存在多样性。因为小波变换的有效性受最优小波函数和小波分解次数的限制，因此在应用小波变换时，需要采用合理的方法来选择小波基函数和分解次数。

1.3 国内外研究现状

零件表面的形貌特征与零件的耐磨性、抗震性、润滑性等重要性质有重要的关系，要想能够准确的对零件的功能特性进行评估，能够掌握零件表面形貌的准确参数是关键。近年来，有许多科研工作者对这方面进行了详实的研究。

华中科技大学的王文东通过理论分析选择了dbN和symN小波函数，利用两种小波基函数对端铣、镗铣加工样件进行重构，选择重构误差最小的小波函数为最优函数，基于MATLAB GUI平台设计了表面形貌参数评定系统^[2]。河南科技大学的李艳娜基于二代线性相移小波变换理论，对小波滤波的提升算法进行了研究，采用了自己编写的、经过改进的小波变换函数，对研磨表面粗糙度工件的表面粗糙度进行分离和评定，计算三维形貌的参数的数值，将应用改进算法计算出来的参数计算结果与仪器测量值进行对比，证明了改进算法的准确性和有效性^[3]。新疆大学的玛合帕丽·努尔旦基于函数的逼近理论，完整地分析了小波理论的建立过程，通过对 Haar 函数的分析，在建立 Haar 函数的小波母函数的基础上，利用 Haar 函数，基于小波空间和尺度空间函数，实现了对原始函数的多尺度重构，证明了利用小波分析理论可重构表面微观几何形貌，且多尺度重构的表面微观几何轮廓的精度高于单尺度重构的精度^[4]。武汉理工大学的周文棣利用高斯滤波和小波滤波对5种具有不同类型的海洋贝壳表面形貌以及特征参数进行比对分析，对高斯滤波和小波滤波的滤波能力和特性进行了分析，并且证明了两种方法用于表面形貌测量的可行性^[5]。

通过对这些参考文献的研究，决定采用小波滤波的方法来搭建本次课程设计所要求的机械零件表面形貌评定参数软件，吸收前人的研究结果，并添加自己的思考和创意，力求使本次毕业设计的结果具有工程实用价值。

1.4 本文研究内容

零件的部分机械性能和使用性能例如耐磨性、润滑性等与零件的表面形貌息息相关，掌握了零件的表面形貌特征就能够更好的对零件的性能进行预测，从而能够更加充分的发挥零件的使用价值，还能够及时发现不合格的零件以规避不合格零件被使用所造成的的经济损失。因此本论文基于MATLAB GUI平台，设计了一款基于小波滤波的零件二维形貌评定软件，可以实现零件表面形貌的构建、表面形貌特征的分离、评定参数的计算和数据储存等功能。主要研究内容包括：

（1）加载零件表面形貌的测量数据，构建零件表面形貌的二维数学模型。利用候选的小波基函数对该数学模型进行分解重构，求得各个候选小波基函数以该数学模型为对象的重构误差，自动选择误差最小的函数作为最优小波基函数，用该函数进行滤波，得到评定基准面，从而得到表面粗糙度的数学模型。

（2）分解次数设置为可人为选择，同时给出当前分解次数下的评定基准面的平均波长和最大波幅的比值，以帮助使用者合理的选择最优分解次数。根据IOS25178-2标准，确定九个可以反映表面形貌特征的参数和一个反映磨损量的参数，设计并优化这些参数的计算方法。

（3）设计数据存储模块，可以将计算得到的数据以预先设计好的格式存入Excel或txt文件中，并可以保存软件当前的运行界面。

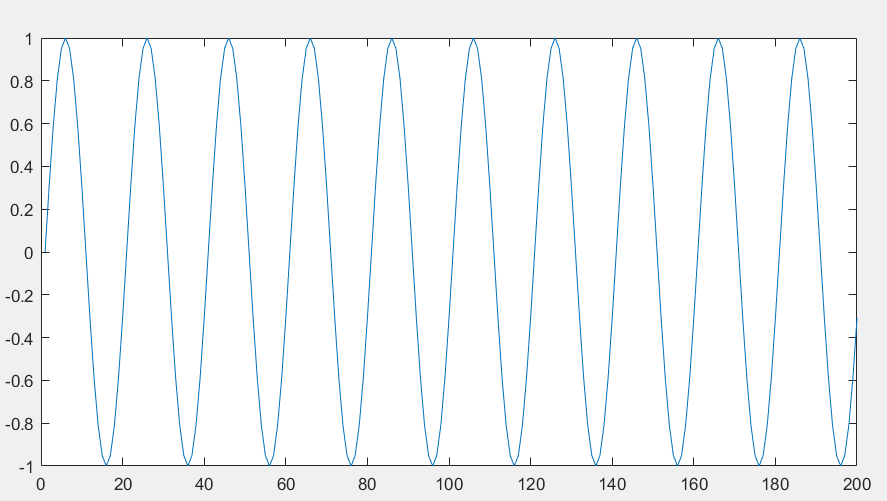
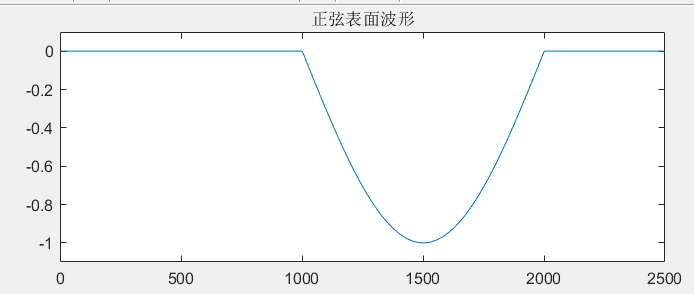
（4）对本设计进行准确性验证。首先假设规律表面（正弦曲线）对滤波的效果和表面形貌评定参数的离散算法进行验证，再假设单个正弦表面对磨损量的计算算法进行验证，再利用车床、刨床、立铣零件的实际表面形貌测量数据对软件评定参数计算的准确性进行验证，发现并纠正算法中的问题，使算法的误差值在允许范围之内。

第2章 利用小波滤波提取表面特征

零件的表面形貌是由零件表面波纹度、零件表面粗糙度、表面形状误差、表面缺陷四个特征复合而成的复杂形貌。要想能够准确的评估零件表面的形貌特征，就需要将原始形貌中的高频信号和低频信号分离开来，从两类信号中分别提取有用的信息。本文将利用小波滤波的相关技术，通过实验的方法确定最优小波基函数和分解次数选择问题，采用小波滤波方法从原始形貌中提取出评定基准面，从而得到粗糙度形貌。

2.1 小波分析的原理与优势分析

傅里叶变换是一种全局的变换，应用傅里叶分析对信号进行处理时，要么完全在时间域对信号进行变换，要么完全在频率域对信号进行变换，因此就无法表述信号特征的时频局部性质,但是时频局部特性是非平稳信号最基本和最关键的性质^[6]。因此为了分析和处理非平稳信号，以傅里叶变换为基础，一系列新的信号分析理论被提出，小波变换就是其中之一。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：