摘 要

随着中国经济市场的发展，债券市场也在兴起，不断出现含有嵌入期权的衍生品，对定价也提出了挑战。在中国债券市场发展的前期，由于发行的债券基本上不会发生违约，信用风险缓释工具发展缓慢，但是随着经济市场的发展，市场上也开始出现债券违约现象，近些年债券违约现象更是频发，2018年债券违约数达到149只再次刷新历史新高。债券违约现象的不断发生也提高了信用风险缓释工具在市场上的重要性，促进了市场上信用风险缓释工具的发展。21世纪计算机行业得到了迅速的发展，计算机的计算速度金融市场上的交易越来越复杂，已经不适合使用人工计算来解决，计算流程逐步脚本化。

本文主要研究对象包括正态分布二叉树模型、蒙特卡罗模型以及生存模型，并对每个模型的应用都给出了相应的软件设计。

关键词：二叉树模型；蒙特卡罗模型；生存概率模型；信用违约互换

Abstract

With the development of China's economic market, the bond market is also on the rise. The continuous emergence of derivatives containing embedded options, pricing also challenges. In the early stage of the development of China's bond market, because the issuance of bonds basically will not default, credit risk mitigation development is slow. But with the development of the economic market, the market is also beginning to appear bond default phenomenon. In recent years, bond defaults are more frequent. In 2018, the number of bond defaults reached 149, again refreshed the record high. The continuous occurrence of bond default also improves the importance of credit risk mitigation in the market and promotes the development of credit risk mitigation in the market. In the 21st century, the computer industry has developed rapidly. The transactions in the financial market are becoming more and more complex. It is no longer suitable to use manual calculation to solve. The calculation process is gradually scripted.

The main research objects in this paper include normal distribution binary tree model, Monte Carlo model and survival model, and the corresponding software design is given for the application of each model.

Keywords: Binary Tree model; Monte Carlo model; survival probability model; credit default swap

目 录

第1章 绪论 1

1.1研究目的和意义 1

1.2国内外研究现状 1

1.3论文基本结构 2

第2章 总体设计方案 3

第3章 对数正态分布二叉树模型及其应用 4

3.1简单债券的定价 4

3.2对数正态分布二叉树模型介绍 6

3.3对数正态分布二叉树模型在债券中的应用 7

3.4利率二叉树的软件设计 10

第4章 蒙特卡罗模型及其应用 15

4.1蒙特卡罗模型介绍 15

4.2蒙特卡罗模型在债券分析中的应用 15

4.3蒙特卡罗模型对含权债券定价的软件设计 16

第5章 生存概率模型及其应用 22

5.1生存概率模型介绍 22

5.2生存概率模型在信用违约定价中的应用 22

5.3生存概率模型对CDS定价的软件设计 25

第6章 总结与展望 29

参考文献 30

致 谢 31

附录A 对数正态分布模型构建利率二叉树程序 32

附录B 蒙特卡罗模型对含权债券定价程序 34

附录C 中债Hermite插值模型 38

附录D 生存概率函数对CDS定价程序 39

第1章 绪论

相对欧美等发达国家，我国债券市场起步较晚发展时间较短，债券市场还不够完善。随着国家经济的迅猛发展，债券市场也得到了快速的发展，债券结构越来越复杂，债券相关的工具也亟待完善。本次毕业设计主要研究概率模型在债券工具包括利率二叉树、内嵌期权债券的定价、信用风险缓释设计上的应用及软件设计。

1.1研究目的和意义

在现代金融迅速发展的过程中，金融衍生产品作为对冲金融投资风险的有利工具，在金融创新的浪潮中得到了迅猛发展，金融衍生产品市场的发展已经成为影响全球经济发展的重要因素，对资产的准确定价是进行投资风险管理的基础。^[1]因此，金融衍生产品的合理定价已经成为学术界及实物界研究的焦点。在众多的金融衍生品中，期权已经占据重要的地位，因此对内嵌期权债券定价具有重要的意义。

2008年美国爆发次贷危机，最终导致金融危机席卷全球。而这场次贷危机的起因就是信用衍生品的滥用。随着经济的发展，我国也逐渐的建立起了信用衍生品，随着经济全球化的发展，风险也逐渐全球化，面临不断出现的债务违约情形，信用风险缓释工具应运而生。信用风险缓释工具是把双刃剑，合理的运用信用缓释工具能够促进中国经济更好的发展。所以研究信用风险定价具有非常重要的意义。

1.2国内外研究现状

由于中国金融市场起步较晚发展时间较短，还有很多地方有待完善，发展金融衍生产品能够使投资者较好的规避投资风险。有关期权定价的研究最早是在20世纪初期，法国数学家Louis Bachelier 在研究股票定价问题时涉及到期权定价。目前期权定价的主要模型有：Black-Scholes模型、二叉树模型和蒙特卡洛模拟法。^[2]

Black-Scholes模型最早是由Fisher Black和Myron Scholes在20世纪70年代提出，该模型假设债券的价格符合布朗运动，运用股票衍生品的定价模型进行模拟定价。^[3]但是债券和股票还是存在区别，债券在接近到期日时其价格趋近于债券的面值。在后面的发展中，学者们开始对Black-Scholes模型不断进行改进，使其尽可能符合实际情况。李丰峰在其论文中对分数阶的Black-Scholes模型进行改进，引进了期权保险精算定价的思想，使其大大的简化了推导的步骤减低了推导的难度；在推导结果的基础上又没对市场数据做太多的假设，推导过程较为严谨，并率先将Black-Scholes期权定价模型运用于企业价值评估。^[4]二叉树模型是由Cox、Ross和Robinstein提出，其假设在整个期限内，债券的价格只有向上变化和向下变化两种，每次向上和向下变化的概率和幅度保持不变。目前交易商最常用的是BDT模型，BDT模型假设短期利率服从对数正态分布，解决了HL模型利率为负值的缺点，并且该模型是无套利的，还适用于对美式衍生品的定价。^[5]BDT二叉树模型需要不同到期期限的即期利率和对应期限的利率波动率作为输入。有关期权的蒙特卡罗法的定价最早可以追溯到1993年，Tilley当时给具有提前执行的美式期权定价采用的就是蒙特卡罗法。由于进行蒙特卡罗模拟需要计算上百万次，计算量巨大，朱彦辑在其文章中对该算法进行了改进，采用并行模拟的方法，提高了计算的效率。

我国债券市场起步较晚，信用风险缓释工具出现的时间则更晚。2010年我国首次推出两款信用风险缓释工具：信用风险缓释合约（CRMA）和信用风险缓释凭证（CRMW），2016年增加了信用违约互换（CDS）和信用联结票据（CLN）。^[6]而欧美等发达国家信用衍生品出现较早，在经过长时间的发展后信用衍生品市场已经比较完善，我们也需要逐渐完善信用衍生品的定价模型。

1.3论文基本结构

本文一共分为六章，第一章是绪论，主要讲述了这个毕业设计的需求、设计目标、研究目的和意义、国内外研究现状及论文结构的安排。第二章主要是对整个设计的方案的阐述。第三章主要讲述的是正态分布概率模型的研究应用及软件设计。第四章主要是对蒙特卡罗模型的研究以及其在对内嵌期权的债券进行定价的应用和软件设计。第五章主要是对生存概率模型的研究以及其在信用衍生品CDS定价上的应用以及软件设计。最后是一章是对整个工作的总结，分析目前还存在的一些问题以及对未来工作的展望。

第2章 总体设计方案

债券是政府、企业、银行等债务人为筹集资金，按照法定程序发行并向债权人承诺于指定日期还本付息的有价证券。^[7]目前中国的债券市场成为仅次于美国和日本的世界第三大债券市场，随着中国债券市场的快速发展，市场上债券的数量也越来越多，需要处理的数据量也日益增加，而债券在未来的表现又具有随机性，所以本次毕业设计主要研究的概率模型有：

1. 对数正态分布二叉树模型；
2. 蒙特卡罗模型；
3. 生存概率模型。

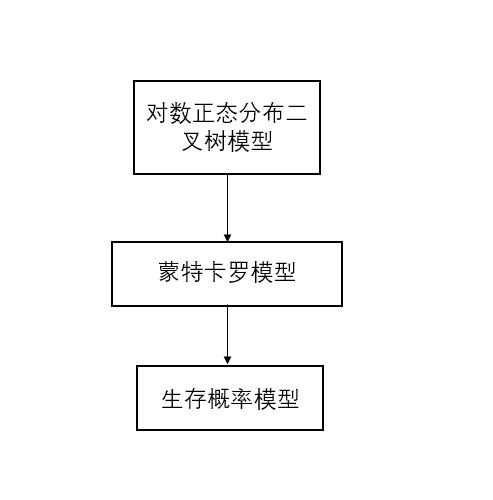整体工作流程如图2.1所示：

图2.1 整体设计流程图

在任务进度安排上将对数正态分布二叉树模型放在最前面，蒙特卡罗模型放在中间，生存概率模型放在最后面，由基础再逐步深入，方便设计任务的进行。

由于Python语言的兼容性灵活性易上手等特点，Python语言的流行程度日益增长，并且在金融研究等方面逐渐表现出越来越重要的地位，所以此次毕业设计我们选择Python作为我们的编程语言。在比较各个Python的集成开发环境后，我们选择PyCharm作为我们的软件开发环境，所有脚本的调试运行均在PyCharm中执行。

第3章 对数正态分布二叉树模型及其应用

本章第一节主要讲述的是简单债券的定价原理，由于后面章节的内容也都是基于债券定价的这些原理，所以只在本章中进行详细的解释，后面不在赘述。对数正态分布二叉树模型由于其分布服从对数正态分布并且其良好的随机预测功能，在金融债券数据处理方面具有广泛的应用，对债券利率的趋势分析、利率路径预测、各种利率结构债券的定价等都具有重要的参考意义。

3.1简单债券的定价

债券的定价就是确定债券的真实价值，债券的价值就是其未来现金流的现值，现值体现了现金流的时间价值。对于单一现金流现值计算公式为公式3.1：

其中为现金流的现值；为现金流；为贴现率；为现金流到现在的时间。

假设一个债券在未来有个预期的现金流，则其现值计算公式为公式3.2：

如果在贴现计算得时候，对于各个时间期限的现金流我们都是采用同样的贴现率，这样的估值方法我们称之为传统估价法。

假定新发行的十年期国债利率是8%，以6%的贴现率按传统估价法贴现则可以计算得到以下数据：

表3.1 利率为8%的10年期国债贴现价值（以6%的贴现率）

*付息方式为半年付

这种估价的方法存在一个缺陷，每期贴现都采用同一个贴现率使其存在套利的空间，而无套利估价的方法则弥补了这个缺陷。无套利估价的方法是将债券的每一个现金流都看成是一个独立的零息现金流，对于不同期限的现金流都采用不同的贴现率来进行贴现，这样就可以避免通过分离债券来获得套利收益。这样的零息利率我们也称之为即期利率。

假定新发行的十年期国债利率是8%，使用无套利贴现则可以计算得到以下数据：

表3.2 利率为8%的10年期国债贴现价值（无套利价值）

*付息方式为半年付

以上即是对简单债券的两种定价方法，很明显如果市场是按传统估价法贴现，交易商们会发现这里面存在套利的空间，他们可以按114.8775元大量按购入该债券并进行分离，对于分离出来每一现金流单独出售，那么对于每一份债券他们就可以获得115.2619元的收入。一份债券经过购入、分离、出售，转手后就可以获得套利0.3844元，这是相当可观的，但是如果市场定价为115.2619元时这个套利的空间也就随之消失。所以对于债券的定价，我们基本上都是使用无套利定价方法。

3.2对数正态分布二叉树模型介绍

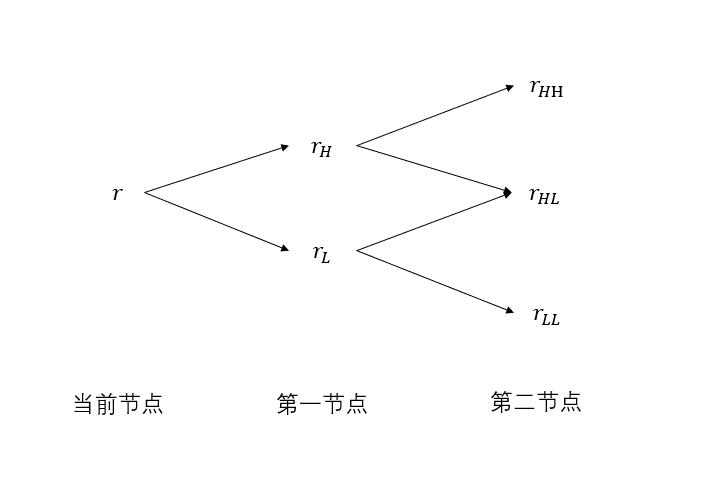
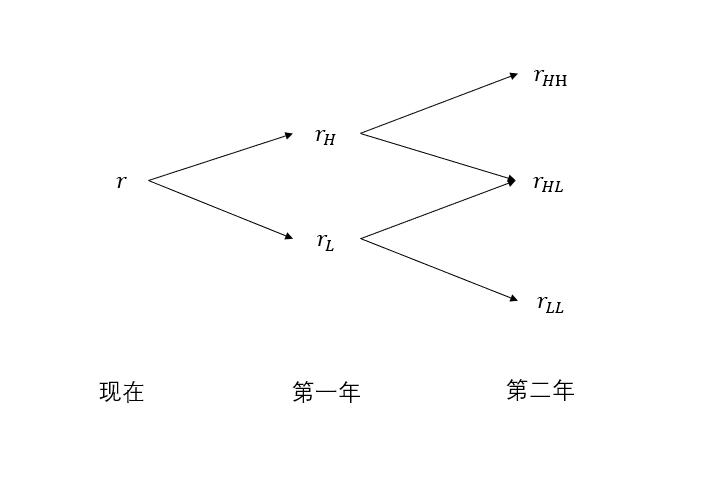
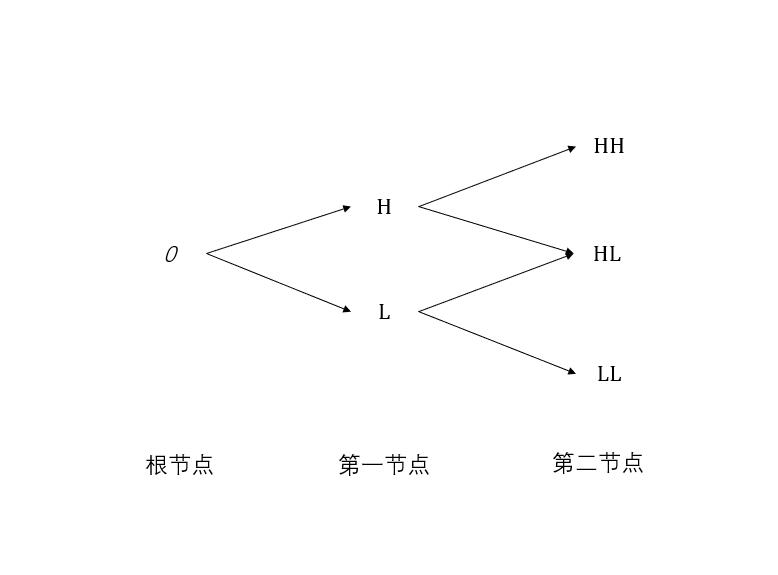目前关于树状模型主要有二叉树模型和三叉树模型，顾名思义二叉树模型即在每一个节点的下一步存在两个分支，三叉树模型则是在每一个节点的下一步存在三个分支，由于三叉树结构复杂研究难度较大，并且目前比较主流的是二叉树，所以我们选择的是研究二叉树。在二叉树的整体结构中会存在向下波动和向上波动次数相同但是排列顺序不同的节点，为了降低难度，我们将只不考虑波动的排序，即二叉树的节点数从根节点往后依次为1、2、3、4…个，具体形状如图3.1所示：

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：