摘 要

在钻井操作过程中，粘滑振动过强会导致钻柱部件过早失效和效率低下。以前的研究工作是通过实时测量钻柱的所有状态并反馈给控制器，然后采取相应控制措施来抑制这种振动。进行这种实时测量在钻柱表面上是较为容易实现的，但当钻柱在井下工作时，其测量结果就会十分有限。为了满足井下状态的要求，本文提出利用扭摆模型来估计井下钻头的位置和速度。在模型的设计中，将非线性的井下摩擦力矩近似处理为线性的持续扰动模型。通过数值模拟法研究该控制方案的性能，仿真结果表明了扭摆模型在识别粘滑振动和估计井下摩擦力矩的能力。

关键词：钻井钻柱；粘滑振动；扭摆模型；仿真分析

Abstract

In drilling operation, too strong stick-slip vibration will lead to premature failure and low efficiency of drill string components. Previous work has been to measure all the state of the drill string in real time and feed it back to the controller, and then take corresponding control measures to suppress the vibration. This kind of real-time measurement is relatively easy to achieve on the drill string surface, but when the drill string works underground, its measurement results will be very limited. In order to meet the requirement of downhole condition, the torsion pendulum model is used to estimate the position and speed of downhole drill. In the design of the model, the nonlinear downhole friction moment is approximately treated as a linear continuous disturbance model. The numerical simulation method is used to study the performance of the control scheme. The simulation results show that the torsion pendulum model can recognize slippage vibration and estimate the friction moment in the well.

Key Words：drilling string；frictional oscillation；The Torsional Pendulum Model；Simulation Analysis

目录

摘要 I

第1章 绪论 1

1.1背景介绍 1

1.2研究现状 2

1.3项目意义 2

1.4论文的组织结构 2

第2章 内容概述 4

2.1粘滑振动（SSV） 4

2.2 钻柱 4

2.3 钻杆与配套结构 5

2.3.1 钻杆 5

2.3.2 加重钻杆、钻铤和方钻杆 5

第3章 动力学理论建模 6

3.1 方案设计 6

3.2 钻柱模型 6

3.3 钻柱振动的力学分析 7

3.4 数学模型在实例中的具体分析 9

3.5 小结 10

第4章 MATLAB/Simulink虚拟仿真 11

4.1 方案简述 11

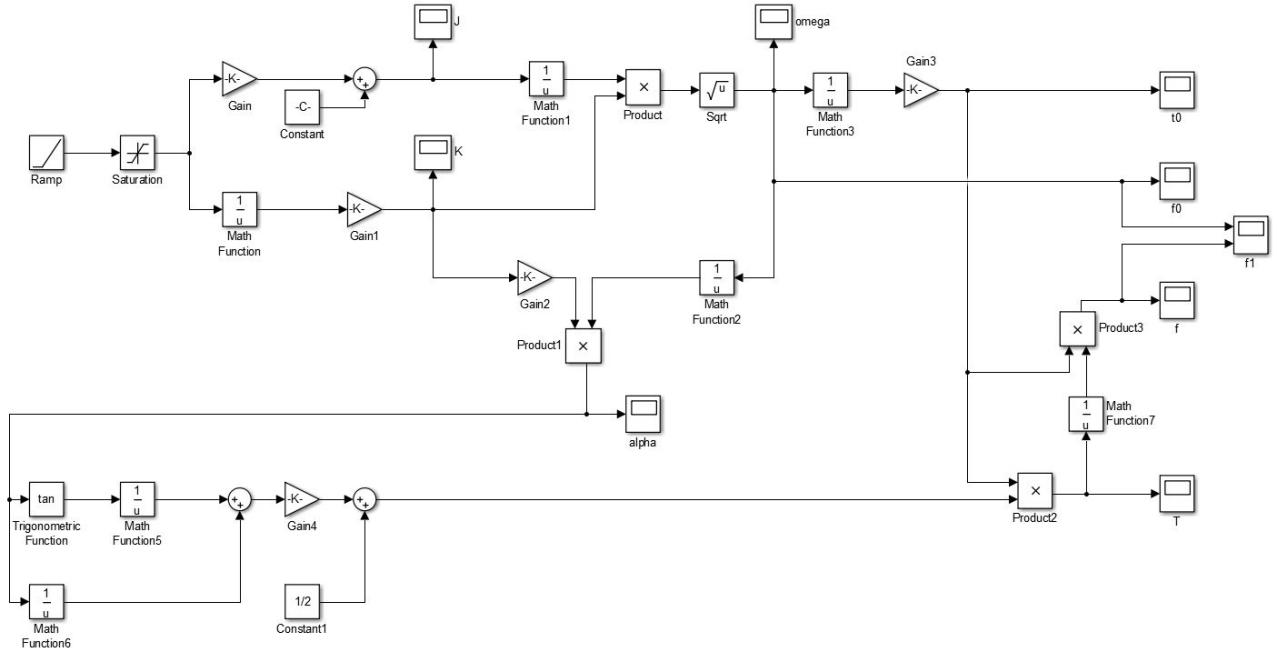
4.2 Simulink建模 11

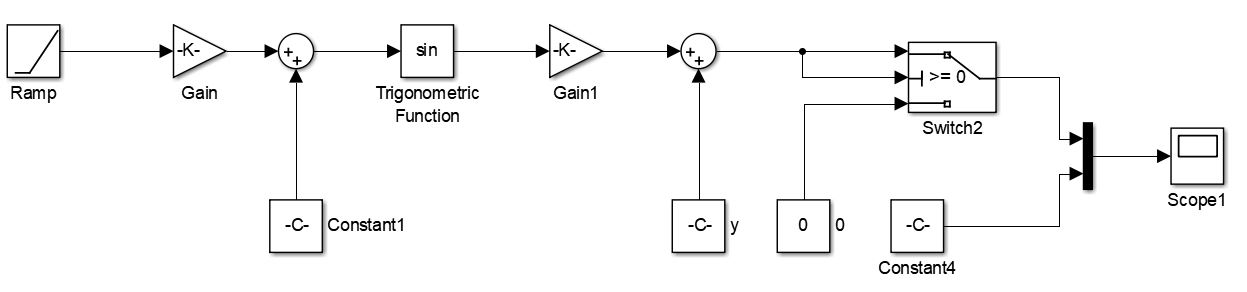
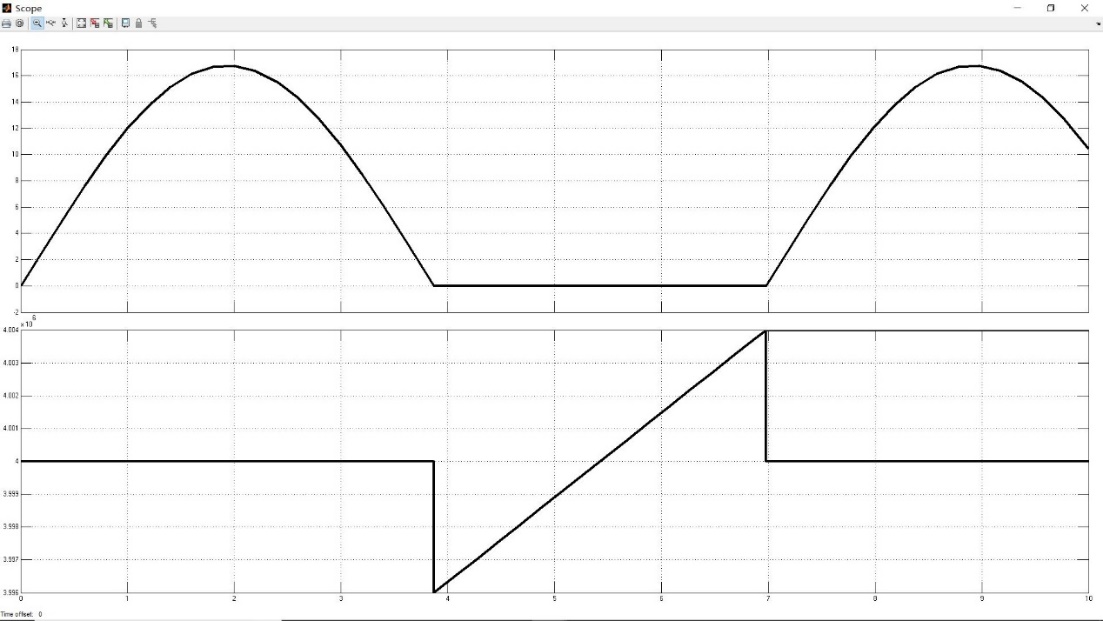
4.2.1钻头转速的变化 11

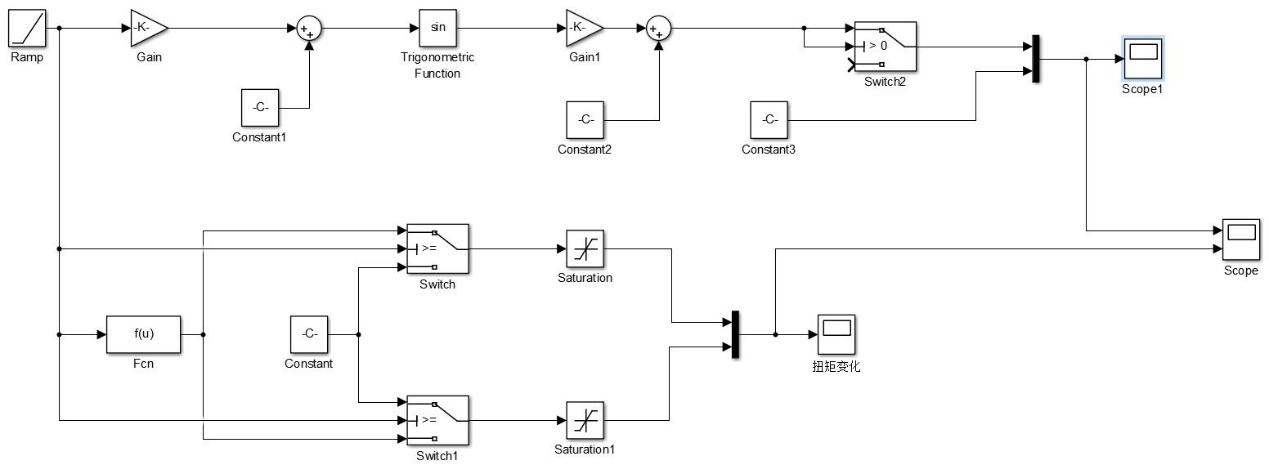
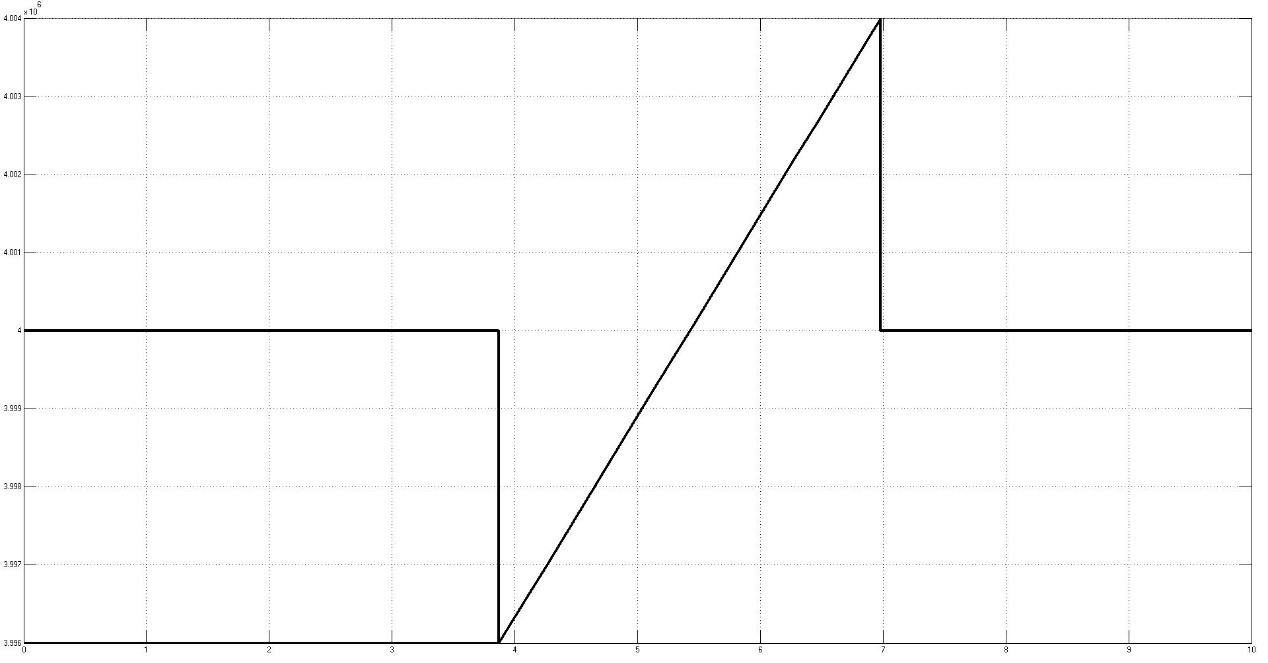
4.2.2钻头扭矩的变化 13

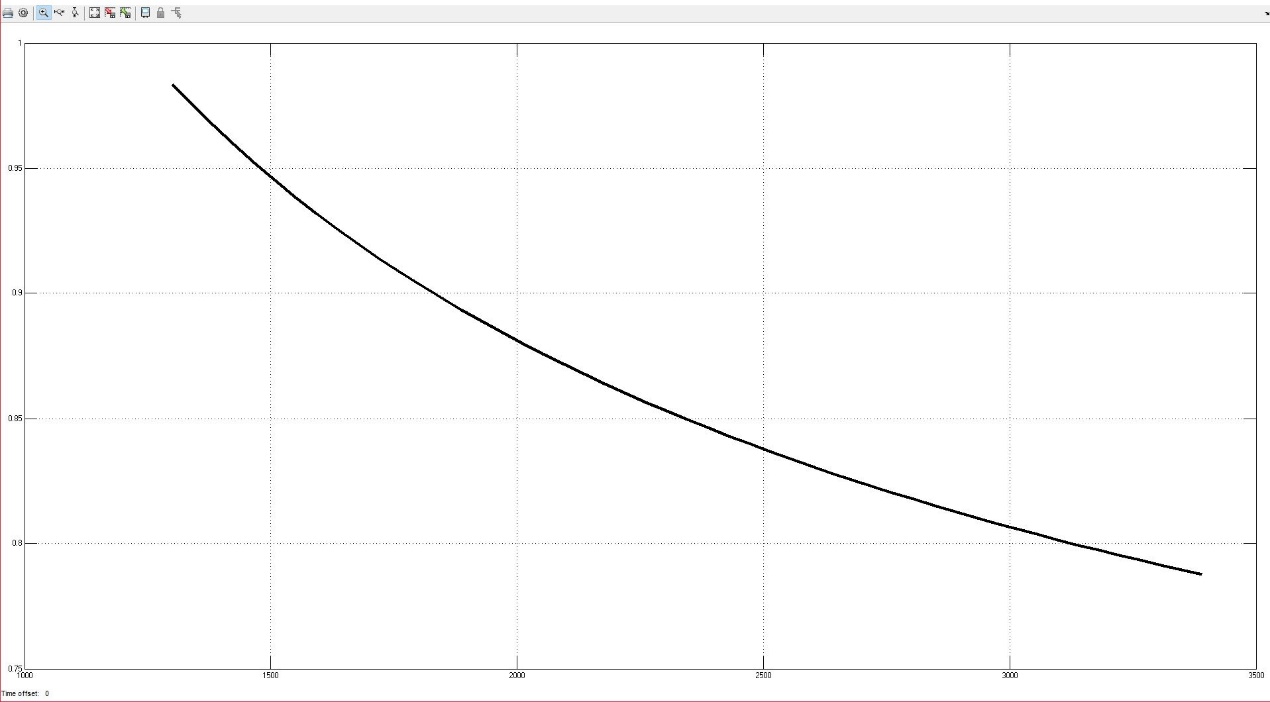
4.2.3长度（井深）影响 14

4.2.4钻头最大转速 16

4.3小结 18

第5章 建模和仿真的后续讨论 19

5.1解决方法 19

5.2误差分析 19

第6章 结论 20

参考文献 21

致谢 23

第1章 绪论

1.1背景介绍

随着石油石化工业百余年的兴盛，现在地下待勘探、待开采的石油储量的分布范围已经由以往的浅层底层转移到了深部地层。以我国西部地区开发时间较长的玉门油田、克拉玛依油田为例，有73%的石油资源深埋于深层地层^[1]。而海上油田的开发区也多为距海面较深的地下。而随着井眼深度的增加，岩层的硬度、密度和塑性也会增大，钻探时底部钻具组合的钻速降低，对岩层的可钻性下降。现场钻采资料显示，井眼深井段钻具的平均转速仅仅能达到靠近上部转盘部分的机械转速的15%~30%，部分情况复杂的钻探区域这个数值甚至只有8%^[2]。以上情况充分说明了现当代油田对石油勘探技术和钻采技术的要求已是与日俱增，而设计和制造出高质量的，能够适应复杂开采环境和具有良好物理学材料学性能的底部钻具系统则成为了面对这些棘手难题的当务之急。

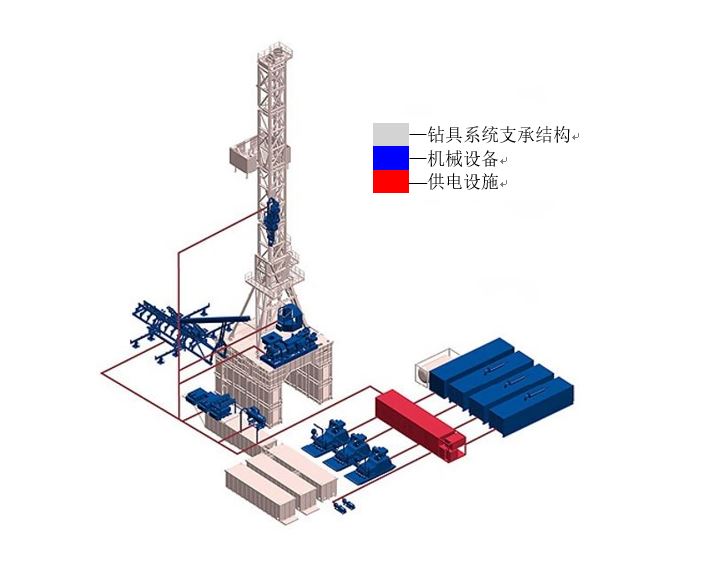
图1.1 钻井平台示意图

为开采深部地层的石油资源，井眼的深度必须随之加深，所需的钻杆长度也有以往的十数节增加到了数十节，开采深度往往超过了3km。对于钻采平台而言，顶部起到驱动作用的转盘的转速会变得很低，在底部钻具组合破除岩层时，会不可避免地产生低频振动。研究表明，低频振动正是造成钻头转速降低的重要原因之一。由于深入地下，这些振动在以往都是难以直接测量和定量分析的，通过研究人员和作业技术人员的模拟分析，我们知道了其中一种对钻具危害极大的振动——粘滑振动^[3]。

粘滑振动又称摩擦振动。在生活中，这是一种可以被人体感官直接感知的振动，在乘坐火车时我们常会有这样的体会：在进站减速时，火车钢轮与钢轨间会产生尖而刺耳的噪音，有时还会直接感受到急剧的冲击和振动，这些令人不愉悦的现象就是摩擦振动造成的效果。在工程上，粘滑振动常表现为低频段的振动，主要是由机械与机械间、机械与加工件的相互作用产生的。长期处于低频振动下工作的机械会有很大的损耗^[4]。在石油钻探方面，由于油气层大都深埋在地层下，开采石油的钻杆长度都超过了千米级，钻头在破岩时会产生强烈的粘滑振动。

1.2研究现状

由于粘滑振动难以直接测量，以往的研究多为依靠建立数学模型来模拟井下的情况。Sellami. H等人的研究结果表明^[5]，粘滑振动是钻头和岩层间的摩擦力造成的。Lin Yaoqun 等人利用简单的扭摆模型，推导出了钻柱能产生摩擦振动的长度规律，并分析了振动幅度和地下岩层摩擦阻尼间的关系^[6]。韩春杰等人研究了钻柱的粘滑振动，并提出钻头克服摩擦扭矩造成钻柱产生振动，随着井深的加深，粘滑振动越容易发生^[7]。Wu Xianping等人的研究表明^[8]，能够产生井下粘滑振动的主要因素是井底钻具组合的转速产生的波动。粘滑振动是钻井钻柱和岩层间一种复杂的摩擦关系，具有非线性和不确定性的特征。

1.3项目意义

在深入地下数千米的位置进行无法现场监控的作业，本身就是困难重重。当地质状况复杂，地下岩层与油气层交错分布时，粘滑振动很容易造成钻头极度损耗甚至钻杆扭转崩坏的情况，轻则数次起钻下钻更换钻具，重则需要重新设计井眼和直斜井段。本次设计的目的就是建立粘滑振动的仿真模型，确定出影响其强度大小的因素，最终应用到实际生产中，通过对某钻井平台已有的钻探资料和地质资料的分析，确定钻井钻具可能受到的粘滑振动的强度，并以此来确定选用强度足够的钻井钻具进行下一步钻探。

1.4论文的组织结构

本篇论文的主旨是通过建立粘滑振动的理论模型来分析这种特殊的振动现象与钻井钻具间的关系。为实现此研究目的，本文将从以下几个部分来作具体探讨。

（1）对石油钻探行业的背景、发展状况和井下作业的难度作了简要的介绍，引出了本文的分析对象粘滑振动，并对粘滑振动目前的研究现状作了简短概述。这一部分具体对应的是正文第1章。

（2）对研究粘滑振动时所涉及的机械名称和专有名词作了解释说明。具体对应的是正文的第2章。在后文中，为使阅读流畅，对于出现频率较高的专有名词，如无特殊说明，“粘滑振动”一词将由SSV代替，在具体特指时仍会使用原名称。“底部钻具组合”将由BHA代替，规则同上。

（3）在前两章的基础工作之后，着重进行对钻井钻具的物理学建模。建模用到的是“扭摆模型”，以方便列出含有模量、扭矩、转动速度、长度和时间等在研究粘滑振动方面重要物理量的方程式。在建立好数学模型后，还会引入实例来对抽象的物理量具体化，以反映出粘滑振动在生产中的特性。这一部分具体对应的是正文的第3章。

（4）第3章中的数学模型并不能直观地展现出各个因素间“变量”的影响，为完善这一数学模型，后文将提出使用Simulink建模软件来对粘滑振动进行分析。其中，钻头转速与时间的关系、钻头扭矩与时间的关系、钻头转速与钻杆长度的关系、粘滑振动频率与井眼深度的关系会是研究和分析的重点内容。这些变量关系各自独立却又相互联系，从不同的方面剖析了粘滑振动的成因和影响。这一部分具体对应的是正文的第4章。

（5）理论建模和虚拟仿真不失为研究难以定量测定的物理量的优势方法，第3、4章中对于钻井钻柱粘滑振动的虚拟仿真已经得出了积极的结论。之后就是回顾这一研究方法，总结其探究成果，同时给出相应的可实施的解决方法。与此同时，作为虚拟仿真，理论值与实际情况总会存在一定的差别，对误差的分析和对仿真可靠性的确认是本文的总结工作。这一部分具体对应的是正文的第5章和第6章。

第2章 内容概述

2.1粘滑振动（SSV）

粘滑振动（Stick-Slip Vibration）是一种非线性的复杂运动，其本质是摩擦振动，是一种会对机械产生损耗的低频率的振动。粘滑运动发生时，机械与机械间的接触面处于完全静止和滑动运动之间的状态，会引起很大的磨损，造成破坏性的振动。在钻井作业中，粘滑振动主要表现在钻柱在启动、破岩及低速掘进时与岩石间的摩擦。

2.2 钻柱

钻柱是油气勘探开发过程中的重要工具，是钻头以上、水龙头以下部分的总称，主要由方钻杆、钻杆、加重钻杆、钻铤和工具接头稳定器组成，钻柱与钻头组成的整体在工程上也称为底部钻具组合（BHA）。

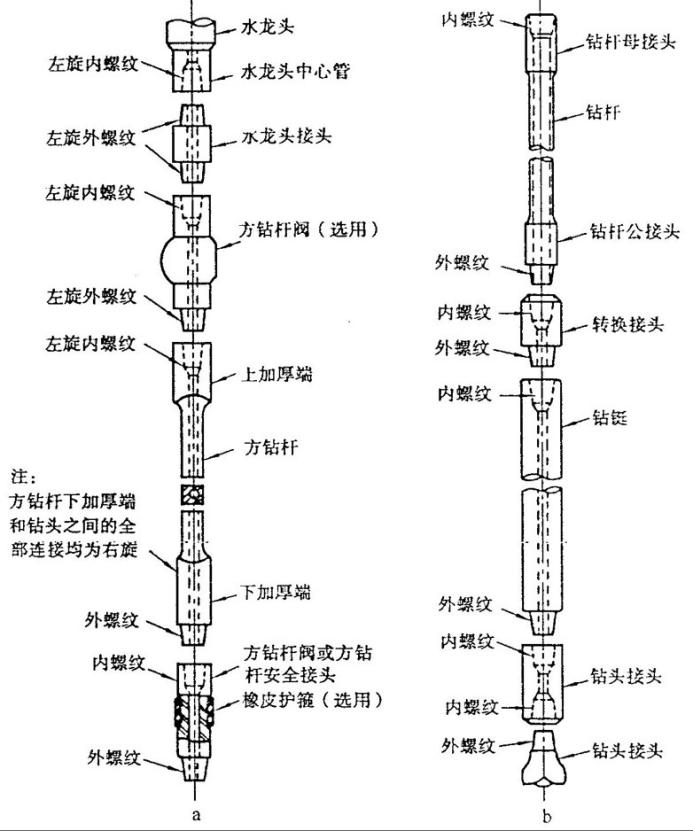在钻井过程中，由多种钻具通过螺纹连接的方式串接组成钻柱，它具有一定的初始曲率和挠度，通过不断地连接不同曲率和挠度的钻杆可以实现井眼的钻井的直井段与曲井段。钻柱的具体功能有以下两点：1.在最上部接连的转盘转动时，依靠钻柱来传递扭转的动能，实现对井底钻头施加压力，以此来破坏地下坚硬的岩层，还能通过联通钻头和转盘的管道间隙来循环钻井液等。2.在井下动力钻井时，井下动力钻具是用钻柱的累加拼接来输送到井底，同时也依靠钻柱来承受地下岩层产生的反扭矩，此外，钻头和动力钻具所需的冷却、清洗液体也是通过钻柱管道和间隙输送到井底的。

图2.1 BHA示意图

2.3 钻杆与配套结构

2.3.1 钻杆

钻杆主要由无缝钢管的管体与模锻成型的接头通过摩擦焊接的方式连接而成，主要承受拉应力。根据无缝钢管材料性能的强度，钻杆分为E75，X95，G105，S135和V150等，钢材牌号后的数字用来表示表示该种钻杆的最低屈服强度，如V150钢表示该钢材的最低屈服强度为150ksi（ksi为应力的英制单位，1ksi=6.895MPa）^[9]。

除无缝钢管钻杆，现在常用的还有铝合金轻质钻杆。这种密度小、耐腐蚀且无磁性的材料在某些特殊情况的油田中有着独到的优势。根据结构不同，铝合金轻质钻杆分为两种：一种是整体式铝合金钻杆；另一种是通过螺纹连接的钢制接头的铝合金管身钻杆，这也是应用最为广泛的轻合金钻杆^[10]。

2.3.2 加重钻杆、钻铤和方钻杆

加重钻杆结构与钻杆类似，但加重钻杆的管壁更厚。加重钻杆具有足够长度的外加厚接头，安装在钻柱下部并连接钻铤，以实现两者的刚度过渡。

钻铤位于整个钻柱的底部，是连接钻柱和钻头重要部件，用以向钻头施加压力，并减轻钻探过程中钻头的晃动。

方钻杆连接在转盘以下，整个钻具的最上部，以连接转盘和钻柱。方钻杆的主要功能是通过转盘的旋转带动整个BHA的旋转，以帮助钻头向下掘进。

第3章 动力学理论建模

3.1 方案设计

SSV是一种非线性振动，具有复杂的特性。为方便研究，可在将误差尽可能减小的情况下对其可做如下假设:

（1）钻柱系统只由钻杆、钻铤和钻头三部分组成，结构为简单柱体且密度均匀；

（2）BHA在作业时产生的扭曲忽略不计;

（3）BHA的质量集中于钻头，钻杆视为一根长直的长度可变的弹簧，钻铤视为一段固定长度的弹簧来处理; 转盘的转速均匀保持不变;

（4）忽略钻井时岩体之外的结构的阻力。

综上所述，本文通过建立扭摆模型来研究粘滑振动的产生方式并建立数学模型对具体事例进行分析。

3.2 钻柱模型

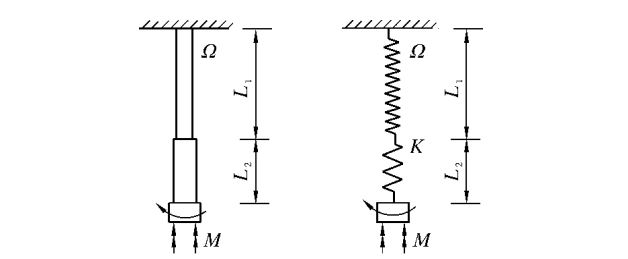通过方案设计中的论述，可建立钻井钻柱系统的简化模型：

a b

图3.1 BHA的力学模型

图3.1a 中J为有效转动惯量，为简化后的一根钻杆的长度，为具有固长的钻铤的长度，Ω为转盘旋转产生的固定转速，M为钻头部分受到摩擦力而产生的扭矩。将图3.1a 的模型进一步简化成图3.1b 所示的扭摆模型，并设K为钻柱部分的扭转刚度。

3.3 钻柱振动的力学分析

钻柱处于粘滑状态时，钻头可以视为质量均匀的轮盘，根据动力学（转动惯量J×角加速度β=合外力矩M，刚度K=力矩/旋转角度）可得以下公式：

（3.1）

其中，为旋转角。

钻杆、钻铤的截面惯性矩可表示为：

（3.2）

其中，、为钻杆的内外径；

、为钻铤的内外径。

钻杆钻铤的有效转动惯量J可以表示为：

（3.3）

其中，为钻柱的材料密度（）；

扭转刚度K可表示为：

（3.4）

其中，G为钻柱的剪切模量（Pa）。

钻头受到的摩擦扭矩可以表示为：

（3.5）

其中，是恒定摩擦扭矩，即钻头进行滑动运动所产生的摩擦力的扭矩。是在滑动摩擦扭矩之外产生的额外部分。为最大摩擦扭矩，即SSV发生的过程中最大静摩擦力产生的扭矩。

根据上述公式可对钻柱的运动作出如下分析。

当钻柱摆脱粘滞时，钻柱开始运动，此时的初始时刻为t=0，其转动力矩M等于最大摩擦扭矩。因此，钻柱运动的初始条件为：

（3.6）

此时由式（1）可得如下方程：

（3.7）

满足上述方程的解为:

（3.8）

其中，为角频率，为相位角:

（3.9）

（3.10）

当钻头发生粘滞时，钻头停止运动，其角速度为0。此时有：

（3.11）

由此可得，当BHA系统第1次停止运动时，滑动经过的时间为:

（3.12）

此时的角位移为：

（3.13）

到钻头再次运动的时刻，粘滑振动经历了一个周期T。T取决于转动扭矩再次达到最大摩擦扭矩的时间。当钻头再次运动时可得:

（3.14）

综上可解得粘滑振动的周期T为：

（3.15）

其中，为扭转的自然振动周期，

（3.16）

则粘滑振动的频率可表示为：

（3.17）

钻头转速可表示为：

（3.18）

最大转速即为：

（3.19）

作用在钻头上的扭矩变化可表示为：

（3.20）

3.4 数学模型在实例中的具体分析

以大港油田张东地区张海井为例，通过技术资料可知该钻井平台钻柱相关参数^[13]。

表3.1 钻柱参数

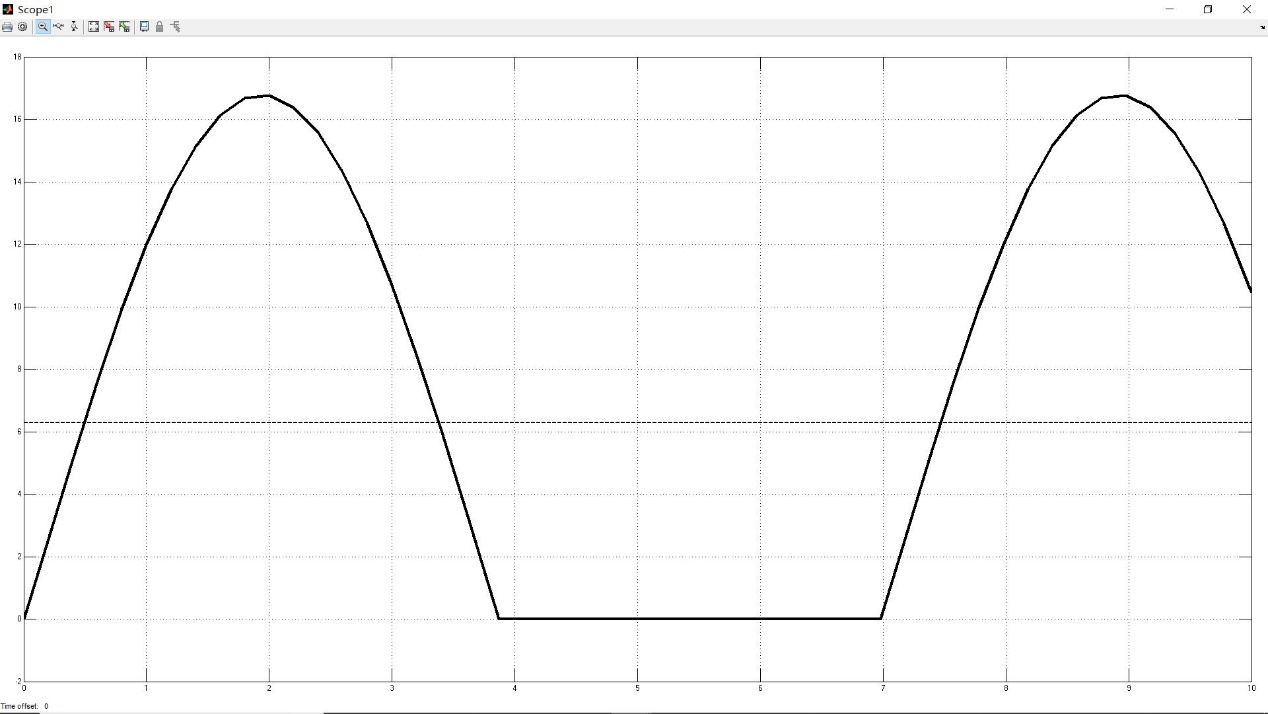
由数学模型可推导算出BHA振动的固有频率= 1.1430Hz，固有振动周期 = 5.4971s。计算得该钻井平台井下SSV的周期 T =6.9778s，SSV的频率 f =0.7878Hz，最大转速可达16.7785rad /s。

3.5 小结

由上述计算可以初步得知：

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：