英语原文共 55 页，剩余内容已隐藏，支付完成后下载完整资料

---

外文翻译

一、汽车悬架

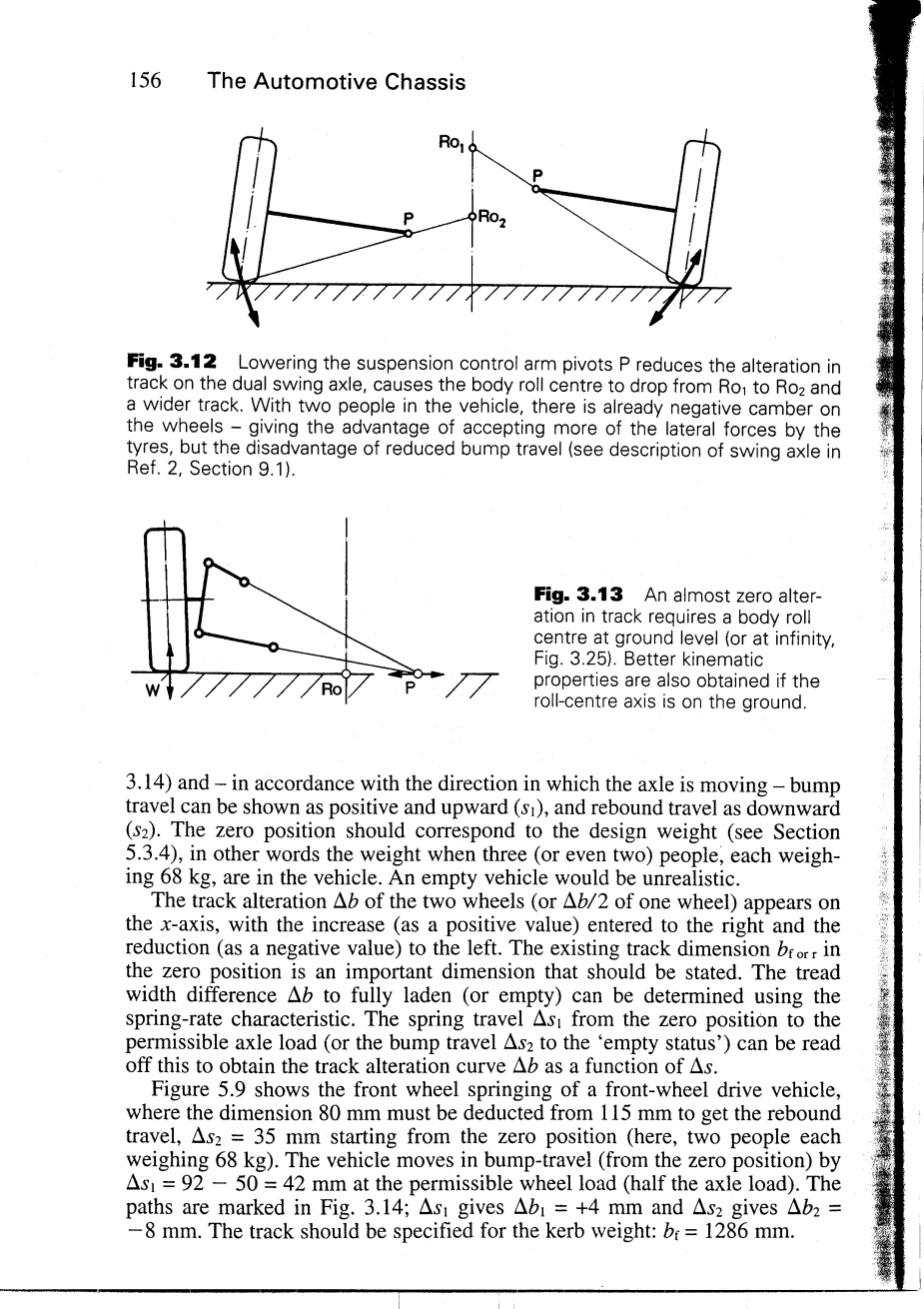
图3.12 降低悬架控制臂支点P，从而降低双摆动轴的跳动轨迹，使车身侧倾中心从RO1点降低到RO2点，并有了更宽的轮距。当有两个人坐在汽车中时，车轮会具有负外倾角-让轮胎能够承受更多的侧向力。但其缺点是减少了弹簧的行程（见9.1小节对摆动轴的描述） 图3.13 要想跳动几乎为零则要求侧倾中心在地面上（或在无穷远处）当车身侧倾中心轴线也在地面时，还能获得更好的运动特性。

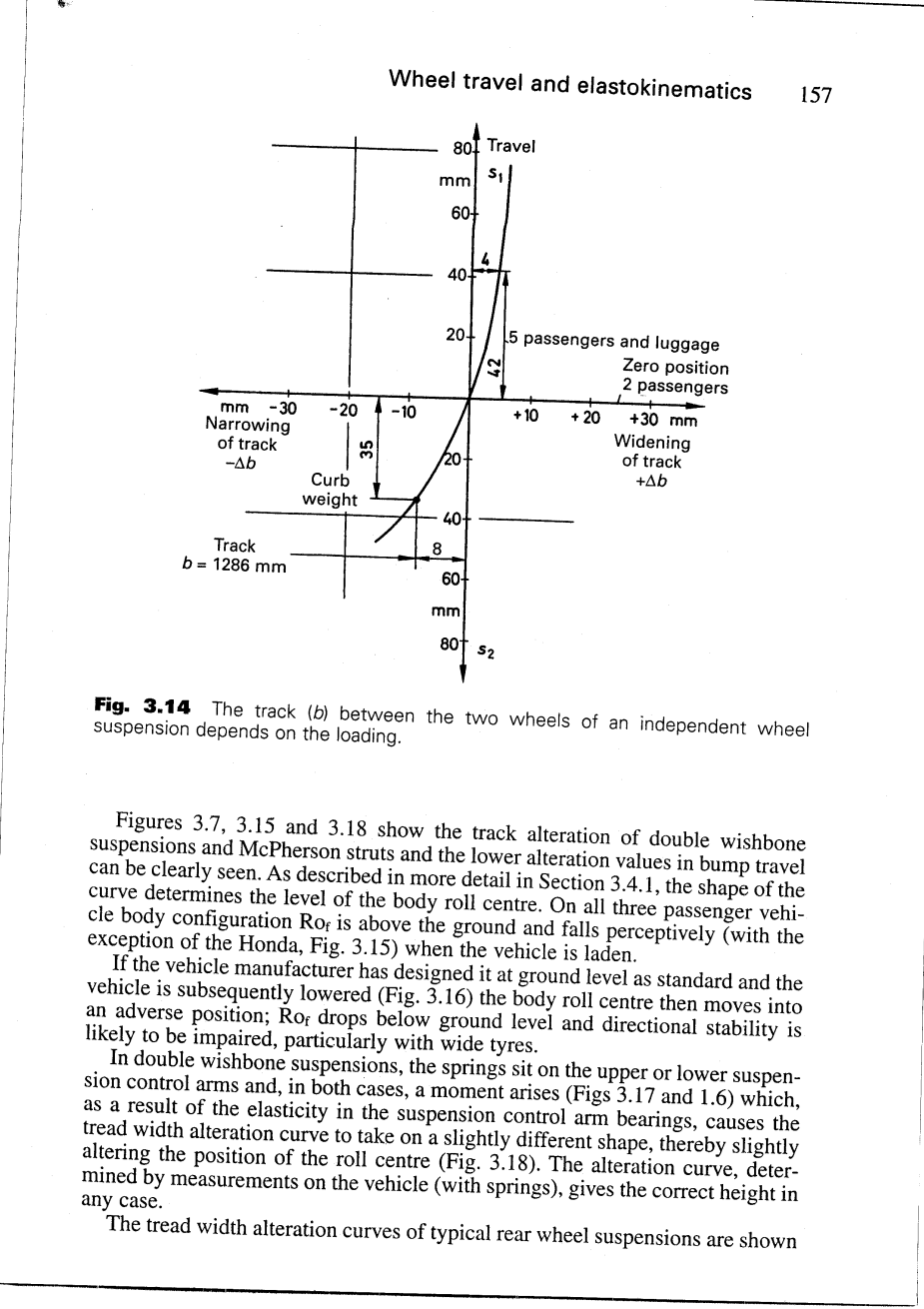
3.14 根据轴的运动方向，我们定义拉伸行程为正，而回复行程为负。那么弹簧原点应该与设计相同（见5.3.4小节），即其重量相当于三个（或者两个），重量为68Kg的人坐在汽车内，只考虑一个空车是不切实际的。

两个轮子的轨迹该变量（或者每个轮子的改变量为/2）在X轴上，并且有右轮增加而左轮减小的趋势。在原点的轨迹尺寸是一个重要参数，胎面宽度在满载（或空载）时的数值可以由弹簧的改变量来测定。利用弹簧从零点到满载的行程（或者零点到空载的行程）可以得到随着的改变曲线。

图5.9表现了前轮驱动汽车的前轮跳动状况，其中必须从115mm的行程中减去80mm来获得回复行程。=35mm 从零点开始计算（两个68kg的人在车内），当车辆在拉伸行程（从零点开始计算），则=92-50=42mm ，在允许的负荷下。其轨迹在图3-14中有标记，由知= 4mm，由知=-8mm。轨迹必须由整备质量求出：=1286mm。

图3.14 独立悬架的两轮之间的轨迹（b）取决于装载质量

图3.7,3.15和3.18表述了双横臂悬架和麦弗逊悬架的跳动轨迹，并可以明显的看到弹簧在拉伸时有更小的跳动。像在3.4.1小节详细讲到的一样，曲线的形状决定了车身侧倾中心位置。当三个乘客在车内时，车身参数在地面上方（根据本田的测试，图3.15），而当车满载时会快速的下降。

如果车身结构设计是以水平面为标准并且降低了侧倾中心，那么车辆容易在不利状况运行，低于地平面，方向稳定性有可能受到损害，对于宽面轮胎尤为明显。

在双横臂悬架中，弹簧坐落于上或者下控制臂，在这两种情况中，当有一个瞬态响应（图3.17和3.16），悬架控制臂轴承弹性影响会导致台面宽度产生轻微变形，从而导致侧倾中心的轻微变化（图3.18）。这个变化由车辆测量决定，在任意的情况都能得到正确的高度。

胎面宽度改变曲线对典型后轮悬架的改变

图.3.15 轮子轨迹是由前置前驱的奥迪A6（1996），欧宝雅特（1996）和本田雅阁（1996）（图1.57,5.52和1.55）测量得到的。本田是唯一一个采用双横臂悬架的乘用车，其运动特性的优点可以明显的观察到。

车身侧倾中心（单位：mm）：

图.3.16 前轴两轮轨迹的测量在大众高尔夫上测得，在通常情况下，其位置由制造商制定，车身侧倾中心在路面附近，降低了30mm意味着车身的侧倾中心往地下移动了115mm，导致车身侧倾中心面更长，在理论上增加了侧倾角度。 但是由于存在保险杠震动，而在视觉上又无法察觉到，其过弯倾角被大大减小了。（见图5.16和5.5.3节）

图3.17 在轮胎接地点的力和作用在下支撑球节的力行成了一个力矩，此力矩被悬架控制臂的横向力 和-抵消。作为简化，我们把上下悬架控制臂看成水平的。

图3.18 两个轮子的轨迹改变，分别用有弹簧和没有弹簧作为双横臂悬架的弹簧行程作用来测量。其曲率的不同，表示可驾驶车辆更高侧倾中心与理论值的区别（不考虑反向的弹簧行程），在画板上计算并绘制（见图3.7）

在图3.12,3.19,3.20和3.74中，非驱动刚性和扭转轴悬架的轨迹会随着弹性外倾角的改变而增加或减少。（图3.55）

3.4 侧倾中心和侧倾轴

在所有独立悬架中，车辆运动轨迹和侧倾中心高度都有直接的联系，所以两者应该被一起测量。见第2章和第9章的详解。

3.4.1 定义

根据德国标准DIN70000，侧倾中心Ro为垂直平面与车轮中心的交点（图3.21），并且其中横向力（沿y方向）可作用在簧载质量上。换句话说，车身在运动时没有侧倾角。

因此侧倾中心就是车辆的中心点（从前面），并且是轴的中心点（从侧面观察时），在该点作用一个横向力时，车身开始发生侧倾，而其中的力被车身和轴吸收。基于车轮的现有变量曲线，侧倾中心R0是车辆的中心点（图3.22），该点被垂直于AB的切线分割，位于车轮接地点的轮廓线上。前轴Ro点的高度（或者后轴）可以由这个方式求出。

图3.19 上图为梅赛德斯后驱汽车的单轮轨迹（见第2章的5.3.4小节），宝马3系（图1.1）和本田雅阁的非驱动桥（图1.55），曲线的形状说明，梅赛德斯的多连杆式悬架在存在载荷的情况下，侧倾中心会下降（图3.22）。质心高度如下：

图3.20 阿尔法·罗密欧的后桥运动学分析，这个测试的是一个轮子的变动。悬架垂直挠度曲线上轴荷和转向的改变说明车辆后轴的侧倾转向有增加不足转向的趋势，这一点通过调节两边车轮的载荷控制连杆可以实现。后轮上降低侧倾中心可以降低在额定载荷下驱动轮的弯曲载荷传递（同前轮的一致），这样就能够让车辆获得更多的不足转向。

刹车反应辅助角和抗点头（对角弹簧）角在图3.16中有显示，轴见图1.15。

图3.21 侧倾中心在车辆正中间（从前往后看），也在轴的正中间（从侧面看）。

图3.22 侧倾中心高度可以用理想载荷下的跟踪变化曲线的正切角来求。

和在正切角度中已经画出来了，由悬架控制臂轴承的弹性作用（图3.18），有如下公式：

= （3.2）

因此车身侧倾中心对一侧车轮有：

前和后

且

=1400mm，每个轮子=6mm，=40mm，= 3.3

在图3.15中，对于奥迪和欧宝，当轮胎受压时，曲线上的正切线永远和Y轴平行，这个和侧倾中心在有载荷的情况下会下降一样，是麦弗逊悬架的一个特点。但是，对于多连杆式悬架的正切角，侧倾中心点R0在受到压力时变化量更小（见本田和图3.18）。这个同样应用于这种后轴（图3.19和3.20）。一般当左右的变形量不同时，车身侧倾中心不在位于车辆的中心。

3.4.2 侧倾轴

前后桥的侧倾中心位置与车辆前进轨迹线一起形成了侧倾轴C（见图3.23），这对车辆的操作稳定性来说是一个重要数据。车辆侧倾中心的高度决定了车轴两边载荷的不同，还通过轮胎加强了车辆的自动转向调节能力，以及最大侧倾角度。这个性质对于车辆的舒适性同样有重要意义，较高的侧倾高度和横向稳定杆能阻止车辆发生侧偏。侧倾中心的位置同样取决于车轮的瞬时速度，通常侧倾中心位于车辆的中心平面上，但当侧偏发生时，侧倾中心位置会在水平和垂直两个平面内发生改变，导致车身承受不必要的外力。一个能均匀改变的侧倾中心能够防止这个力的出现。

侧倾中心的高度和车辆行进时侧倾中心位置的改变总是伴随着下列条件的影响：

·用转弯时车轮载荷的变化来实现车辆的自我调节；

·忽略车轮行进的轨迹变动对于汽车轨迹的影响；

图3.23 通过前后侧倾中心的直线C代表了理论侧倾轴（这里还有一个角度），表示质心到质心与地面垂线与线C交点D的距离。这个角度对该车的刚性后桥有益，对于前后轴都拥有独立悬架的车辆，其侧倾中心轴应该只有一个很小的角度。（见公式6.7和6.24）

·弹簧刚度太高影响舒适度

·理想或最大外倾角改变

·作用在车上的应力越小越好

·侧倾轴的位置

侧倾中心轴应该稍微向后偏，这样能够充分利用摩擦力来实现车辆偏航时的回正作用。独立悬架的侧倾中心高度标准为：

前轴h=30~100mm，后轴h=60~130mm

需要特别注意车轮载荷和牵引力的重叠，应减小过大的横向力作用。

根据运动轨迹曲线的曲率可以知道，侧倾中心在有载荷的情况下会有一个更小或者更大的角度。（图3.15,3.19,3.20和3.22）

底盘的设计首先要设计侧倾中心的高度（根据轨迹求得），然后才能设计一个合理的后轴，独立悬架的可以稍微高一点。

如果该车配有刚性车轴，那么车辆将会受到更小的抗侧倾力（图1.23），改结果由弹簧的有效距离以及轨迹变短导致，为了改善这一点，建议把后轴的侧倾中心设计的稍微高一点（像在图3.23中显示的一样）。这一点的可行性可以在第二章中找到。

图3.23中的直线AB是实际的侧倾轴，该轴基本上与地面平行。更加精确的定位取决于转向控制杆的角位置。车身在横向力的作用下向AB倾斜。

图3.24 由双横臂悬架计算并且画出来的轨迹和p，与一个铰链上的纵横切轴（图1.1和3.32）

3.4.3 独立悬架的车身侧倾中心

P（瞬心）点的高度决定了侧倾中心R0的高度（图4.24）。如果P点在地面以上，那么R0同样也会在地面以上。正如图3.22中看到的一样，轨迹曲线上零点的切线随着其与垂线夹角alpha;的变化而变化。但是该点曲线形状取决于实际瞬心和轮胎接地中心的距离。该距离越远，曲率的变化越不明显，外倾角的改变也越小（见第3.5.2小节）。下面的数据显示了如何决定侧倾中心高度，以及如何画出P的轨迹。瞬心到轮胎接地中心的距离q可以通过简单的测量计算求得。

（3.4）

正如在3.24和3.7中看到的一样，双横臂悬架的转向轴位置是十分重要的。这条连接内外转向臂中心点的直线需要延长来连接瞬心P，同时，P点与轮胎接地中心W的连线在车辆的中心面上通过侧倾中心R0.对于平行的控制臂，P点的距离是无穷远，并且一条平行于控制臂的线需要在W点被画出（图3.25）。

图3.25 双横臂悬架的侧倾中心，其质心在无穷远处。

图 3.26 如果悬架旋转控制臂与另外一个从侧面看有一定的角度，首先应该过E1与G1点做地面的垂线，该线与旋转轴C1C2和D1D2的交点为E2和G2，从后视图来看的话可以用于计算瞬心的位置。

当瞬心与轮胎接地中心的距离很远时，建议用图3.24的方法计算距离p和。转向控制臂从侧面来看是倾斜的（这样的设计是为了获得纵倾轴，图3.155），过E1和G1做垂线（图3.26），这样可以获得E2和G2的位置，从后视图来看与E1和G1相连。通过瞬心P点到轮胎接地中心的直线经过了侧倾中心（如图3.24）。如果该轴被横向的板弹簧控制，并且在中间位置，那么力臂L3对于计算侧倾中心极为重要，并且当弹簧与两点相连时，弹簧接触点到轴的距离L2也极为重要（图3.28）。更加详细的内容可以在4.7.3.1小节查阅。

图3.27

集中固定式钢板弹簧R0和P的位置确定

图3.28 两处支撑的低钢板弹簧R0和P的确定方法

图3.29 台面宽度越大，侧倾中心R0就越高，图中的例子是麦弗逊悬架

在麦弗逊式撑杆或者阻尼支柱上，过车身一侧的E点做减震活塞杆中心线的垂线，延长转向控制臂的中心线，该两条线相交于P点。（图3.29）图例还显示了把延长到后侧倾中心位置从RO1移动到了RO2。若地面上有负的主销偏移距则要求把铰链位置移动到更加接近轮胎的位置（图3.102），这样就把主销轴线和减振器中心线分割开了。图3.30显示了轨迹EP，这条线与减振器轴线垂直，并且并不是独立于转向控制臂的，这个对于汽车的运动性能是一个决定性的参数。建议在悬架控制臂处于水平状态时计算和p，因为瞬心会远远超出了画板的范围（图3.22），第4.7.3.2小节有更多详细的内容。

在纵向控制臂轴上（图3.32），E点的运动方向（崔志宇悬架旋转控制臂轴）十分重要。通过E点做CF的平行线可以得到P点和R0点。该计算见图3.24 。在麦弗逊支柱中，侧倾中心的高度会被低悬架控制臂的角度影响，并且当控制轴EG和麦弗逊支柱之间的角度变化时也会发生轻微的改变，这是此类型悬架的一大劣势。在纵向控制臂轴线上，增加旋转轴CF的角度，从而增加R0高度是可行的。同时，瞬心距离轮胎越近，轮胎在受压时会有一个更加大的负外倾角，这点优势非常明显。

图 3.30 麦弗逊支柱与阻尼器之间的垂直度越高，GD1也就越平行于水平面，侧倾中心R0也就越贴近地面。当轮胎在压缩行程时，这会对外倾角产生一个不利的影响。延长下控制臂（从D1到D2）提高了车辆运动性能。

为了让转向主销内倾角有一个偏量，G点必须画在轮胎外，这样有益于减小平面b上的垂直力，b的距离越短，活塞杆和导向杆之间的摩擦力也就越小，D,E,G之间的力也就越小（见图1.11）。Q表示胎面宽度需要被限制。图1.8表示了E和G的精确位置。

b的长度计算很容易：

（3.4a）

根据设计可知，无论是对于 还是-,都必须整体带入公式中（见第三章的7.2小节）。

根据图3.24和3.32求出的质心高度只有在高载荷时一致，该点可以被旋转，但同时也是不固定的，并且仅当侧倾角度达到2度时。利用橡胶元件的弹性可以在小范围内调节车辆的高度（图3.18）。计算和研究表明，车身侧倾角度很大时，左右轴线的角度不同，但是车身内的侧倾中心会发生一个的改变。当车辆上坐了行人时，该偏移量会达到20mm。

图3.31 在麦弗逊支柱和减震轴上轨迹和p的计算。

图3.32 对于纵横向悬架，应该过E点做平行于CF的直线，该线与GD的延长线的交

剩余内容已隐藏，支付完成后下载完整资料

---

资料编号：[148223]，资料为PDF文档或Word文档，PDF文档可免费转换为Word