牵制平衡算法案例研究毕业论文
2020-02-19 18:31:21
摘 要
仿生算法是仿生学在算法领域的应用。它是一种通过模拟自然界现有的行为机制而实现的优化算法。仿生算法具有很强的适应能力和处理大量数据与高复杂度问题的能力。本文通过对生态平衡机制的模拟,提出了一种新的仿生算法:牵制平衡算法。其灵感来源于对地球这个涉及数百万生物体的庞大的生态系统如何实现长期的稳定平衡的思考。地球生态系统具有惊人的复杂性,我们难以通过数学分析的方法去获得令人满意的方法从而实现生态平衡这一目的。然而自然界通过最简单、智能的生态平衡机制,实现了所有生物间的稳定动态平衡。在这里我们模拟并简化这一机制来构造牵制平衡算法,其中涉及变量被视为种群物种,种群的规模和或数量与涉及变量的值相对应。我们构造了牵制平衡算法的自增长函数,相互依赖函数,资源约束和算法的规则,并通过数学分析的方法证明了此算法的收敛性。接着将算法的思想应用于标杆问题——背包问题和TSP问题的解决,并与其他算法如遗传算法,模拟退火算法等进行比较试验来证明了算法的有效性与可靠性。该算法易于实现,特别适用于解决复杂系统优化中的大型问题,并将其思想与其他算法所结合来提高获得更优质解的概率。
关键词:仿生算法;生态平衡机制;优化问题;NP-hard问题;遗传算法;模拟退火算法;牵制平衡算法;复杂系统
Abstract
Bionic algorithm is the application of Bionics in the field of algorithm. It is an optimization algorithm realized by simulating the existing behavior mechanism of nature. Bionic algorithm has strong adaptability and ability to deal with large amounts of data and high complexity problems. In this paper, a new bionic algorithm is proposed by simulating the mechanism of ecological balance: the restraint balance algorithm. Its inspiration comes from thinking about how the earth, a huge ecosystem involving millions of organisms, can achieve long-term stability and balance. The earth's ecosystem has amazing complexity. It is difficult for us to obtain satisfactory methods through mathematical analysis to achieve the goal of ecological balance. However, through the simplest and intelligent ecological balance mechanism, nature achieves a stable and dynamic balance among all organisms. Here we simulate and simplify this mechanism to construct a constraint equilibrium algorithm, in which the variables involved are considered as species of the population, and the size and number of the population correspond to the values of the variables involved. We construct the self-growth function, interdependence function, resource constraints and rules of the algorithm, and prove the convergence of the algorithm by mathematical analysis. Then, the idea of the algorithm is applied to the benchmarking problem, knapsack problem and TSP problem. Compared with other algorithms such as genetic algorithm and simulated annealing algorithm, the effectiveness and reliability of the algorithm are proved. This algorithm is easy to implement, especially suitable for solving large-scale problems in complex system optimization, and combines its ideas with other algorithms to improve the probability of obtaining better solutions.
Key words: bionic algorithm; ecological balance mechanism; optimization problem; NP-hard problem; genetic algorithm; simulated annealing algorithm; constraint balance algorithm; complex system
第1章 绪论
在计算机科学、自动化、管理和工程技术等领域里人们经常会碰到组合优化问题,其中的很多问题如旅行商问题,指派问题,车间作业调度等都已经被证明是NP-hard问题。用传统的单纯形法非线性规划这些基于数学的优化方法是很难解决此类问题,随着问题规模和复杂度的增大,所耗费的计算时间和将呈指数增长,且要求目标函数有较为严格的数学特性,这极大地限制了其应用的范围。为了获得解决这类问题的优良方法,科学家们开始着眼于我们生活的自然界。
1.1 研究目的与现状
自古以来,自然界就是人们创造工具和工程方法的最大的灵感源泉,如飞机,雷达等,这些推进人类社会发展的东西无不来自于自然的启发。当科学家们花费数十年的时间去科学研究或者创造发明时,他们会惊奇地发现这些惊世骇俗的设计早已存在于自然界之间,而模仿自然也早已成为解决各种科学或社会困难问题的一个捷径,由此就催生出了仿生学。仿生学这个词语起源于上世纪60年代,某些生物有机体具有的功能比迄今而至任何人工制造的机械都要优越许多,仿生学就是一门要在工程上实现并且应用优秀的生物功能的学科。例如在信息的接受(感觉功能)、信息的传递(神经功能)、自动控制系统等方面,这种生物体的结构与功能给了人们许多关于机械设计的启发。仿生算法则是仿生学在算法领域的应用,即通过模仿自然界中生物的行为和机制来构造一个算法从而达到解决人类生产生活中实际问题的目的。由于这些算法在求解时不依赖于梯度信息,其应用范围很广,在一些大规模的复杂问题中都表现出相对传统方法极优的性能。因此,他们的出现为解决NP-hard的组合优化问题提供了一条全新的路径,近些年国内外的研究学者也开始越来越关注这种新兴的算法。
经过数十年的研究,如今较为成熟的仿生算法已经很多了,如遗传算法、人工神经网络技术、模拟退火算法、模拟退火技术和群集智能技术等。人工神经网络是在对人脑组织结构和运行机制的认识和理解的基础之上模仿其结构和性能行为的一种工程系统。遗传算法则是根据生物进化理论的原理发展起来的一种广为应用,高效的随机搜索与优化的方法。模拟退火算法则来源于固体退火原理。与传统的优化方法相比,这些仿生算法在解决NP-hard问题上有着明显的优越性。而每一种仿生算法在解决不同种类的问题时都有着它自己独特的优势。通过模拟生物世界中生态平衡的机制,我们提出了牵制平衡算法这一新的算法,它在解决一些特定问题方面有较强的适应性和优越性。本文主要通过解释其基本思想与原理,两种标杆问题的案例应用和与其他算法的对比来验证算法的有效性。
1.2 课题研究内容
第一章:主要介绍了仿生算法的研究背景及研究意义,目前已有的仿生算法和本文提出的牵制平衡算法的思想来源。
第二章:首先对牵制平衡算法的原理进行基本介绍;接着利用数学建模的知识简略证明算法的收敛性。
第三章:将牵制平衡的思想应用背包问题和旅行商问题这两个标杆问题的解决中,来验证算法的有效性。并与其他的仿生算法进行对比分析各自的优劣。
第四章:归纳全文,对整个课题研究和论文进行总结性的阐述,并针对研究过程中发现的问题提出需要进一步讨论的建议。
第2章 牵制平衡算法的原理与数学模型
2.1 算法的起源
从第一个生物诞生起到如今地球生物圈这个庞大的生态系统,自然界总是用它最基本的法则去解决那些极其复杂的问题。生物从单细胞体到拥有高等智慧的人类的进化是通过遗传的选择,交叉,变异和适者生存等来实现的,这也造就了现在多元化多样性的地球。而遗传算法就是受其启发,通过模仿生物的进化过程来解决工程中的一些实际问题。
与遗传算法等其他仿生算法一样,牵制平衡算法的灵感也来源于自然界的点滴中。我们知道所有的生物都有自己的生存方式,而如此多的生物种类和庞大的生物数量是如何和谐地生活在地球这个生物圈中,这可以当作是一个复杂度很高的数学问题,以人类目前的技术还不足以能够解决。而神奇的大自然只利用一个简单的机制——相互牵制,便达到了这一个巧妙的生态平衡。所谓牵制,即在事物皆有关联的情况下,两种或多种事物之间所产生的一种相互限制的关系,包括此消彼长,物极必反等。举个简单的例子,一片草地与一个羊群,在没有人为因素的干扰下,超过一定阈值后,草的数量会随着羊数量的增多而减少,而增多的羊群由于食物限制逐渐进入一个逆增长的模式,此时草的数量又会有一定回升,如此长此以往,循环往复,最终进入一个动态的平衡,即羊与草的数量都处在一个稳定的范围内波动,两者之间达到和谐。这就是所谓的牵制平衡。
牵制来源于物种间的关联与依赖,万物皆有联系,或远或近或紧密或疏远,任何现存的事物的状态都受与之关联最紧密的那些事物的影响。自然界既是生命的调节器,也是一台超级计算机,它所创造的所有的平衡都不是随机的,而是和物种的初始状态,规模和繁殖能力,外界因素等息息相关的。由于复杂度和能力原因,本文只研究关于两种生物间的平衡数学模型,并以此为基础建立牵制平衡算法。
2.2 算法的基本思想与数学模型
牵制平衡算法的基本思想是把生态平衡当作优化目标,将达到平衡时各种群的规模(数量)作为问题最终的优化解。各种群平衡后所能达到的可能规模就是需要优化的问题的解的空间。每个设计的变量都有一个自增长的特性,而各变量之间则存在着依赖性,变量间的牵制和自身增长的相互作用与限制使得整个系统达到最终的动态平衡,而变量最终的数值就是优化的输出解。
我们利用一个最简单的生态平衡关系来建立数学模型——羊吃草。真实的生态平衡机制在这里很难用数学模型完整地表现出来,我们只能通过建立较为简单的数学模型和符合实际的个体趋势来提炼出牵制平衡的思想。
首先,我们先分析各个种群在资源和环境是理想状态下的生长规律。例如羊群,当草的数量足够大时,因为食物充足的关系,羊群是会不断增长且增长量是随着羊群数目的增加而增加的,即可用如下式子表示:
其中为下一时间阶段羊群的数量,为目前阶段羊群的数量,表示一个恒定的增长率,表示时间间隔
同样,如果当草地的规模相对羊群规模足够大的时候,作为食物的草的被捕食数量可忽略不计,只需要考虑草地的自增长。在这里我们设定草地的密度一定,那么草的数量就只与草地的面积有关,草的数量可用如下式子表示:
其中为下一时间阶段草的数量,为目前阶段草的数量,为恒定的增长量,只与草地的初始状态有关,表示时间间隔
现在考虑两者之间的牵制关系,牵制表示的是两者之间的内在依赖性,在这个简单的生态系统中,由于羊与草是捕食者与被捕食者的关系,草是这个系统赖以维持的资源,而作为系统中另一个角色的羊则需要消耗草以保持自身种群的生存,两者间相互依赖的起点就是一定数量的羊吃掉一定数量的草,即草的数量的减少是与羊群数量的大小成正比的,数学关系如下:
,
其中表示单位时间内被消耗的草的数量,它是由该时间段内羊群的数量所决定的,我们可以利用积分公式来表示,表示单位数量的羊所消耗的草的数量。
在这个生态关系中,羊群实际的增长速率是与羊群规模和草的数量规模之间的比例关系息息相关的,当羊群数量和草的数量比例相对较小时,羊群拥有充足的食物资源,其增长速率将呈现一个较高的水准,随着时间的推移当比例逐渐增大时,因为资源限制的关系羊群的增长率会慢慢减少,若这个比例大到超出一个临界值,羊群也会出现负增长的情况。这一过程可以用如下数学式子模拟:
,
这就是两者间的牵制关系的函数。其中为自然底数,表示一个比例系数。
因为生态系统中的资源是稳定且有限的,在经过上述过程的循环往复后,生态系统最终会达到一个动态平衡的状态,即各个种群的数量都会在一个稳定的范围内波动,而这个动态的平衡是依据资源的性质所定的。在羊吃草的例子中,最终羊群和草的数量的规模是初始的时候草地的面积就决定了的,草地初始的面积越大,各种群最终所达到的平衡的规模就越大。
算法的原则是通过模拟设计变量的大小作为生态系统中不同生物的规模,建立设计变量的自增长函数和设计变量之间的依赖关系来表现的。输入设计变量的初始值,即各种生物体的初始大小,然后根据自生长函数和相关性进行迭代。设计变量的值将随着时间的推移而更新,这意味着种群规模将得到更新,当设计变量的值在一个给定范围内相当长的一段时间内保持稳定时,生态系统将被视为处于动态平衡状态。设计变量值作为最优解输出。
2.3算法收敛性证明
关于本算法的收敛性证明在此不赘述
第3章 牵制平衡算法的案例应用
算法的收敛性证明了之后,需要将它应用于实际问题中检验其有效性,在这里我们采用两种标杆问题即背包问题和旅行商问题的求解来验证牵制平衡算法的效果,并与其他算法如遗传算法,退火算法等进行对比,分析各自的优劣性。
3.1 旅行商问题
旅行商问题,也就是TSP(traveling salesman problem)是一个经典的组合优化问题。经典的旅行商问题可以描述为:一位销售人员要去若干个城市推销本公司的商品,他需要从一个城市出发,经过所有的城市后回到出发地点,应该如何选择行进的路线以使得总的行程最短?从图论的角度来看,该问题实质是在一个带权完全无向图中,找一个权值最小的Hamilton回路。由于TSP问题的可行解是地图上所有的点的全排列,随着点的个数的增加,解域就会成几何倍数扩大,产生的解的组合就会爆炸。旅行商问题是一个NP-hard问题,由于其在物流配送、工厂调度、电路板线路设计以及交通运输等领域内有着广泛的应用,国内外的学者对其进行了大量的研究。早期的研究者使用精确算法求解该问题,常用的方法包括:线性规划法、分枝定界法、动态规划法等。但是,随着问题规模的增大,精确算法将逐渐变得力不从心,因此,在后来的研究中,国内外学者重点使用近似算法或启发式算法,主要有遗传算法、蚁群算法、模拟退火法、禁忌搜索算法、贪婪算法和神经网络等。
3.1.1 遗传算法求解
我们首先用遗传算法求解这个问题,遗传算法是以达尔文的进化论和孟德尔的遗传学说为基础,模仿自然界生物进化的机制而发展起来的随机全局搜索和优化算法。其本质是一种高效、并行、全局搜索的方法,它能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应的控制搜索过程以求得最优解。遗传算法操作中以优胜劣汰为原则,在潜在的解决方案种群中逐次生成一个近似最优解的方案,在遗传算法的每一代中,根据个体在问题域中的适应度值来进性个体选择,并通过从自然遗传学中借鉴来的再造方法产生一个新的近似解。由于遗传算法是一种进化算法,根据其启发式算法的特点,并不能保证得到问题的最优解。其求解效果与初始种群的选择,基因编码方式,个体选择方法和交叉变异规则等因素都有关。遗传算法应用于TSP的基本思想是对求解问题进行编码从而模拟基因的性质以便后续交叉和变异的操作,通过交叉与变异可以得到新的个体,再计算新个体的适应度,从而判定是否保留或舍弃当前的个体。在经过多次的循环往复后就可以留下适应度值最优秀的个体,通过解码即可得到问题的近似最优解(不一定是全局最优解)。
遗传算法的基本步骤是:
- 初始化。随机选择一些个体组成最初的种群,地球最原始的生命也是随机产生的。在MATLAB软件中实现的时候我们通过产生随机数来实现这一过程。
- 评估。通过某种方法来评估个体的适应度,也就是个体的生存能力。一般我们设定一个量化的函数来进行此过程,使目标结果更优的个体适应度更高,存活下来的几率也就更大。
- 选择。类似于自然选择,优良的基因、生存能力强的被选择留下来的概率会更大,当然也存在着逆袭的情况。在代码中我们通过轮盘赌法来实现这一过程。所谓轮盘赌法,又称为比例选择方法,其基本思想是各个个体被选中的概率与其适应度值成正比。将所有个体适应度值总和起来作为分母M,即基数“1”,各个个体适应度值除以M即得到被选中的概率,再进行0-1之间随机数r的产生,判定r所落的积累概率区间内,由此来决定被选中的个体是哪一个。
- 交叉。产生后代,基因交叉,可以理解为有性繁殖,自带会从父母那分别得到部分基因,从而产生一个全新的个体。在MATLAB中通过cross函数来实现。
- 变异。后代的基因可能会产生变异,有可能是一个基因位的变异,也有可能是多个基因位的变异。变异在生物进化,特别是新物种的产生中起了很大的作用。在MATLAB中通过mutation函数来实现。
3-5步是产生新种群的步骤,新群体再进行评估,然后再选择、交叉、变异,一直循环2-5步最终找到一个近似最优解。遗传算法的流程图如下;
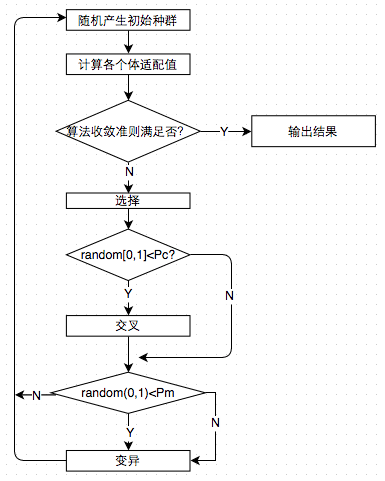
图3.1
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: