三维DEM模拟螺旋输送机散料运输

— Yoshiyuki Shimizu 和Peter A. Cundall

摘要：利用三维离散元数值分析法（DEM）是为了检查螺旋输送机的性能。特别是水平和垂直类的模拟研究，与以往的工作和经验公式的结果进行了比较。结果分析，这种方法可以很好的对螺旋输送机的性能进行分析。

简介

螺旋输送机用于运输散装物料已有一段时间，其组成为，螺旋叶片，驱动轴，驱动装置，壳体U型槽或管道等等。物料输送原理：依靠材料与螺旋叶片的摩擦。螺旋输送机的优点是结构紧凑，维护简单，运输能力强，持续运输，安全性高。另一方面，缺点是长度有限，不能运输粘性较大和块状材料。螺旋输送机不仅可以用作散装运输设备来运输材料，也可作为建筑和采矿机械，例如，用于隧道挖掘机，用来清理土壤或岩石。

对螺旋输送机进行了改善性能和开发新类型的许多研究（Own 1936;Uematsu等. 1960; Hokao 等. 1974）。这些研究大多数是自然实验。此外，他们的理论组成部分只是简单地处理一个部分的相互作用，或单一的物体和所接触机器部件之间的静力平衡。还有，在实际设计中，预测结果基于实际机器数据库(Colijn 1985; Woodcock 和 Mason 1987）里的一个经验公式，这一预测确定因素之一是材料特性。

三维离散元法的数值分析（DEM）可以出色的模拟螺旋输送机动态粒子的运动与相互作用。DEM（Cundall和Strack 1979）在模拟粒子组合方面成为一个有效的数值工具，特别是岩土材料如岩石、土壤和颗粒材料[ Cundallet 等 (1982) Kawaguchi et 等 (1992), Williams 和 Mustoe(1993), Anandarajah (1994), Chang 等. (1997), Iwashita和Oda (1988), 和 PFC (1999)]。应用DEM分析散装装卸设备，包括螺旋输送机，表示机器的组件部分必须表示出来，以及粒子之间的相互作用必须考虑。幸运的是，很容易分析这些物体几何形状。本文，螺旋部分是加在一起的两圆柱，对应于螺旋输送机的部件：螺旋叶片，套管，传动轴。这种方法比起那些具有多平面特征的且具有代表性的物体显得更精确，更有效率。如果螺旋和圆筒的连接由多平面构成，结构的边缘的连接点将导致颗粒不规则运动。此外，由于每块平面和颗粒接触摩擦大大增加了计算工作量。

这项研究的重点是横向和纵向的分析螺旋输送机。与以前的结果进行理论和实验的比较，定量考虑，如颗粒运动和运输材料的结构以及容量，扭矩和功率。此外，设计新的机构，重点对螺旋输送机的主要组成部分—螺旋，进行说明。

机器部件的描述—“spiral”DEM

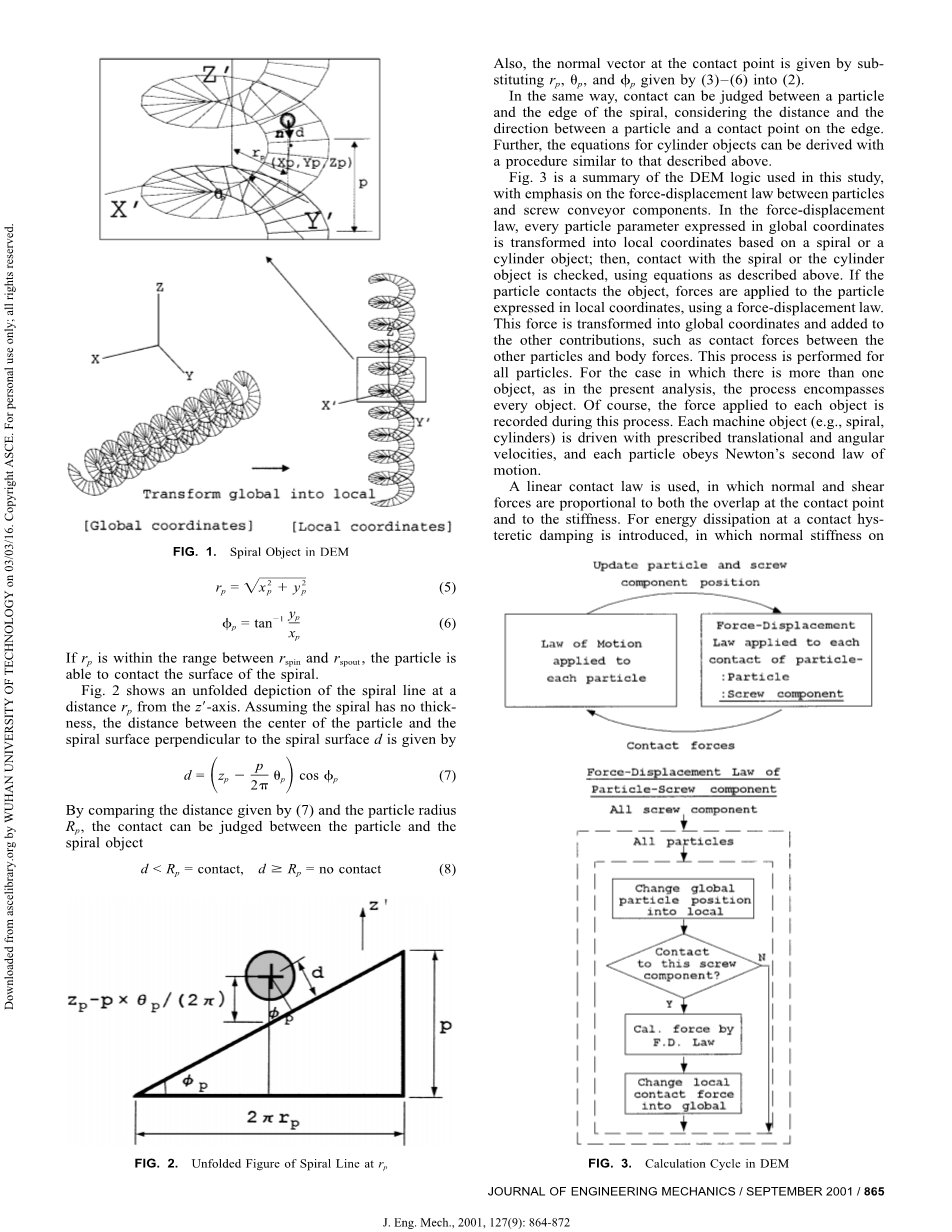
参照图1，定义局部坐标系通过X，Y，和Z轴，原点位于螺旋体中心轴线，本地坐标系与变换矩阵的全局坐标有关。在局部坐标系中，螺旋对象的参数由下式确定（1）

其中p =螺距；

r为半径（内径）[ rspin，rspout（外径）]；

theta;=X 轴在X-Y平面内角度（0，2pi;）。

给出了该螺旋对象的正向量

现在把一个粒子的位置表示为（XP，YP，ZP）局部坐标。Z轴rP的距离和X轴旋转角度分别表示为

如果rP是在rspin和rspout之间的范围内，颗粒能够接触螺旋面的表面。图2显示了螺旋线的展开， RP到Zrsquo;轴的距离。假设螺旋没有厚度，粒子中心与螺旋面的垂直距离为

通过比较（7）和粒子半径的距离可以判断，颗粒和螺旋形物体接触情况。

此外，在接触点的法线向量由Rp，theta;p，Phi;p取代。

以同样的方式，可以判断一个粒子和螺旋的边缘之间的接触，考虑边缘的粒子和接触点之间的距离和方向。此外，圆筒对象的方程可以推导出类似上面描述的过程。

图3是本研究中使用的DEM逻辑综述，重点研究了颗粒与螺旋输送机组件之间力的位移规律。在力-位移规律中，每一个在全局坐标系中表示的粒子参数被转化为局部坐标系基础上的螺旋或圆筒，然后使用上述描述的方程检查螺旋或圆筒接触对象。如果使用力-位移法，粒子接触物体，力被施加到粒子在局部坐标系中，这个力被转化为全局坐标并加入到其他的运算，如其他粒子和自身之间的接触力。这是所有粒子的演算过程。对于有更多的研究对象的情况下，如在本分析中，该过程包括每一个对象。当然，过程中会记录每一个物体施加的力。每个机器对象（例如，螺旋，圆筒）的有规律的运动，并且每个粒子遵循牛顿第二定律。

使用线性接触法，正交和剪切力在接触点的叠加对刚度是成正比的。接触滞后耗能引入了阻尼，在卸载时正刚度大于加载时正刚度。两粒子或粒子和螺杆元件之间接触前后相对速度的滞回阻尼是独立的。将恢复系数设置为0.9，用参数校准，并确定两个刚度之间的比率。为了保持数值稳定性应由最高刚度计算时间步长，库仑摩擦定律在剪切方向上消耗。在这项工作中使用的刚度（KN，KS）是材料EC（PFC 1999）中的杨氏模量。

模拟使用个人计算机（300兆赫英特尔奔腾处理器，英特尔公司，圣克拉拉，加利福尼亚州）和PFC3D 2.1版（Itasca咨询集团有限公司，明尼阿波利斯）上面所描述的一些附加功能。

水平螺旋输送机经验公式及前人理论

由输送设备制造商的以下公式（那不勒斯，佛罗里达州）介绍了材料运输净功率Pnet（colijn 1985；伍德科克和梅森1987）：

在这个公式中，物质因素Fm对应于颗粒与螺杆组分的摩擦系数，材料的性能取决于材料的性质；共四类，即1-4类，在其中Fm的变化0.5至1级为1级，3至 4级为4级。飞行要素Ff和搅拌因子Fp为各种螺旋形态提供校正因子。

Uematsu等人（1960）为粒子和螺旋或圆筒之间的平衡导出方程。图4显示卧式或小型螺旋输送机粒子与螺旋之间的自由体图。在粒子保持稳定状态的情况下角theta;0（称为临界角）只在z方向上移动，（11）（13）是由各方向的力平衡方程。

替代材料的性质和螺旋角为（11）-（13），对临界角theta;0求值。使用体积质量而不用粒子，它的中心重力代替螺杆的外半径。在轴方向的速度（定义为传输速度）Vt，所需转矩Tq，总功率计算为式（14）-（16）。式（14）的导出速度是螺旋速度Pv/（2p）

模型

图5显示了一个螺旋输送机且表1提供了主要尺寸。该模型由一个不同直径的螺旋和双套筒组成。螺旋由螺丝代替，套管和传动轴由气缸代替。这些组件都是4米长。四个参数研究螺旋间距和螺旋与壳体之间的间隙对研究的影响，参考案例有一个间距为直径比0.75为无关案例。

表2列出了材料属性。球形颗粒用以代替沙子作为运输材料，用密度2.65克/立方厘米和15–35毫米的尺寸分布。有效直径D10为21毫米，铜均匀系数是1.5。颗粒的数目设定2500至10000个来检查负载因子，定义的影响取决于块体质量的截面面积与在外壳的空间系数，一般在0.15和0.45之间。

正常和剪切刚度的颗粒接触都是5.0times;10⁶ N/M，这些值远小于式（9）中使用的完整的杨氏模量的10 - 50Gpa。减少接触刚度减少的原因是考虑岩石碎片的表面附近裂缝和一般的退化情况。这些表面因此比完整的材料脆弱从而更容易变形。用于螺旋输送机的部件，正常和剪切刚度2.0times;10⁹N / m，式（9）用杨氏弹性模量和5毫米厚度钢材。

图6显示了三轴试验模拟相同的材料性质的水平和垂直螺旋输送机仿真的结果。体积质量的内摩擦角很大程度上取决于颗粒间摩擦系数。即使是使用较大的摩擦系数，体积质量的内部摩擦角与实际材料相比如沙子，还是比较小的。此次螺旋输送机仿真，颗粒间的摩擦系数是0.7，用以弥补较低电阻。此外，颗粒之间和颗粒与螺旋输送机部件之间的摩擦系数是0.6，这相当于在Uematsu等人的实验研究。（1960）介绍了一种模拟的滞回回弹系数0.9。

参数的计算进行以下检查：（1）螺杆转速（15，30，45，60转）；（2）材料含量（2500，5000，7500，10000颗粒）；（3）螺杆螺距比（0.75），（1）和（4）在螺杆和套管之间的间隙（0、37.5和75毫米）。

仿真过程如下。指定数量的粒子放置在螺旋输送机的半段内的随机位置，受到重力作用下降，达到平衡后，套管不动，螺杆和驱动轴在指定的，恒定的角速度下旋转三周。

结论

图7显示了典型的初始和最终的配置阶段。使每个粒子的运动和混合条件可见，从底部开始在每个级别设置一个不同的颜色，粒子每10%横截面面积分一次类，很明显，颗粒正向前移动，而在自由表面以一定的角度在水平面与螺旋方向旋转。

图8，从侧面显示了从初始阶段到旋转3周后的计算结果。几乎所有粒子向前移动三个螺距的距离。随着粒子数的增加，粒子占据上部区域，然后，有些颗粒穿过驱动轴。如图9所示，在从0.75到1改变螺距直径比的时候运输配置有一些差别。

图9显示了三个旋转结束后的计算结果。对于7500多个粒子，粒子在传动轴上移动。这意味着一些粒子沿螺旋向后移动。随着粒子数增加，临界角也增加。这是因为块体质量由许多粒子组成，动态地阻止每个球形粒子与彼此旋转的粒子的运动。

图10显示了为了克服粒子运动的摩擦，螺旋和驱动轴的扭矩和功率。在启动时需要大的转矩和功率，以加速原先不动的粒子。启动后，虽然有轻微的波动引起的随机组件中的每个粒子的运动，但很快到达稳定状态。

图11显示了计算临界角。临界角是指横截面面积上的角度，从垂直线到散装质量主轴线之间的角度。实心线显示来自（11）-（13）静力平衡的临界角。计算结果是远小于静力平衡。在这个分析中，使用球形颗粒。这些颗粒在螺旋输送机组件中滑动随旋。这是类似于休止角的模拟，其中组件比球形的颗粒具有较小的休止角。也有证据表明，球形粒子与组装体的摩擦系数几乎与颗粒间的摩擦系数无关（Skinner 1969）。虽然静力平衡预测的角度是独立的旋转速度，但临界角随转速的增加而略有增加。

图12显示的是计算的传输速度和来自（14）的比较。随着转速的增加，传输速度呈线性增加。虽然计算结果显示与式（14）相比速度稍小，但具有相当高的一致性。实际上，颗粒不仅在轴向移动，在径向和旋转方向上也有移动。随着粒子数的增加，一些粒子向后移动

移动到驱动轴上，在这种情况下，计算速度变小。

图13显示了计算能力与式（16）的比较，计算出的临界角

和重心被替换，计算出的功率大于式（16），并显示几乎有15%的偏差。一个原因是，粒子动态移动，所以，需要电力来加速粒子。此外，当粒子数增加时，计算出的功率和式（16）之间的差异变大。这是因为（16）不考虑整个传动轴的粒子向后运动，以及驱动轴与颗粒的摩擦旋转的动力。比较了式（10）计算的功率（总功率）和净功率，F_m为1.0。净功率与总功率相比，与之相对应，效率接近85%。如前所述，螺旋输送机不仅在轴向方向运输散装物料，而且还可以在其他方向移动粒子。

图14显示了螺旋与套管之间的两种间隙的整体功率图。上图显示的是37.5毫米的间隙，相当于平均粒径的1.5倍的结果，较低的图显示的是75毫米的间隙，相当于平均粒径的三倍。这些结果和零间隙比较，如图10所示，结果为1.5倍平均粒径情况下呈现出较大的功率波动。这是因为在粒子直径的三倍间隙情况下，一些颗粒粘在该地区在螺旋与套管之间。

垂直螺旋输送机过去的理论

hokao等人（1974）提出粒子和螺旋或套筒之间的静态力平衡方程。图15显示垂直螺旋输送机中粒子和螺旋组件之间的自由体受力图在。（17）-（19）为各方向的力平衡方程。

替代材料性能和螺旋角为式（17）-（19），从在轴向方向的粒子速度分量的反正切函数的推导的角度，在旋转方向（定义为转移角度）求gamma;的值。另外，利用重心代替了螺旋的外半径，颗粒在轴向的速度方向（定义为向上的速度）是由下式推导出的。

模型

图16和表3显示了垂直螺旋输送机的模型和主要尺寸。该模型是由一个螺旋和两个套筒组成，轴向方向是垂直的。模型的主要尺寸与hokao等人的实验（1974）相同，除长度为1.33米，相当于20圈的螺旋（20倍的间距），以获得稳态条件下的垂直散装物料的运输。类似水平的情况，从底部开始在每个级别设置一个不同的颜色，粒子每10%横截面面积分一次类。

表4显示了材料属性。在水平螺旋输送机中用球形颗粒代替砂体分析。粒度分布是4–8毫米，均匀系数C_u为1.4，有效粒径d10为5毫米。粒子数为5000。颗粒正常和剪切刚度是1.2times;10⁶ N/M。这些值通过（9）中0.1Gpa的杨氏模量估算。而且，颗粒之间和颗粒和螺旋输送机组件之间的摩擦系数分别为0.7和0.6。进一步，调整滞回阻尼，使恢复系数等于0.9。

仿真过程类似于水平螺旋输送机。也就是说，5000个粒子最初创建在螺旋输送机的下部，受重力后下降。粒子运动后达到稳定状态，螺旋和驱动轴以规定的速度旋转20周，设置速度在100和500转之间的不同值。

结论

<p

剩余内容已隐藏，支付完成后下载完整资料</p

英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[152825]，资料为PDF文档或Word文档，PDF文档可免费转换为Word