摘 要

圆柱绕流在实际工程中的应用是十分广泛的，有重要的工程应用背景，如水流对桥墩、海洋钻井平台支柱、桩基码头等的作用，风对烟囱、圆柱型建筑物、高压输电线的作用。圆型双柱结构在圆柱绕流现象中是较为常见的一种结构，在工业工程中的应用也非常广泛。

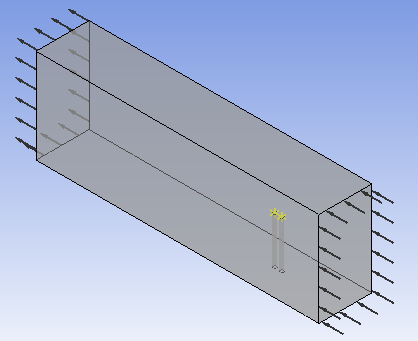
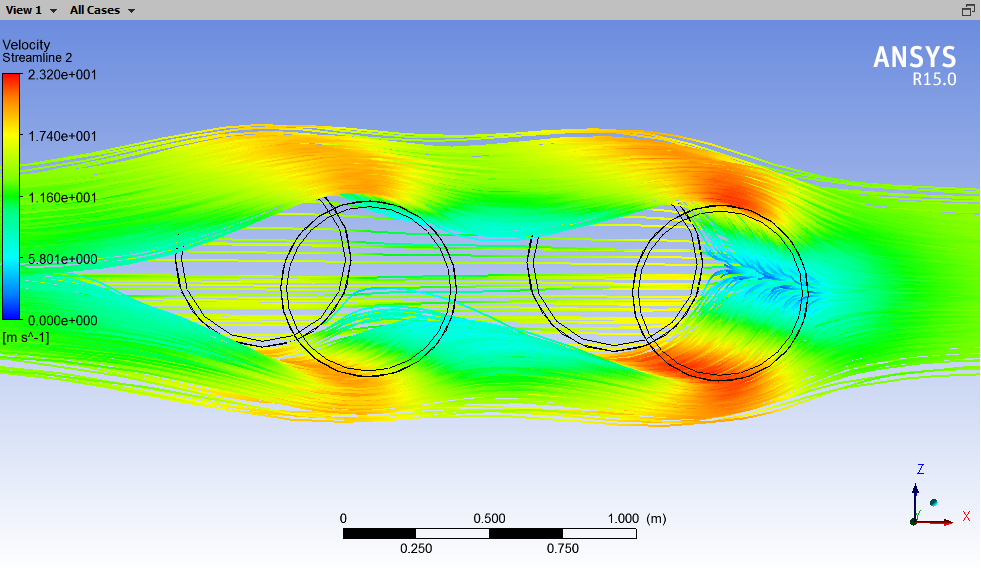
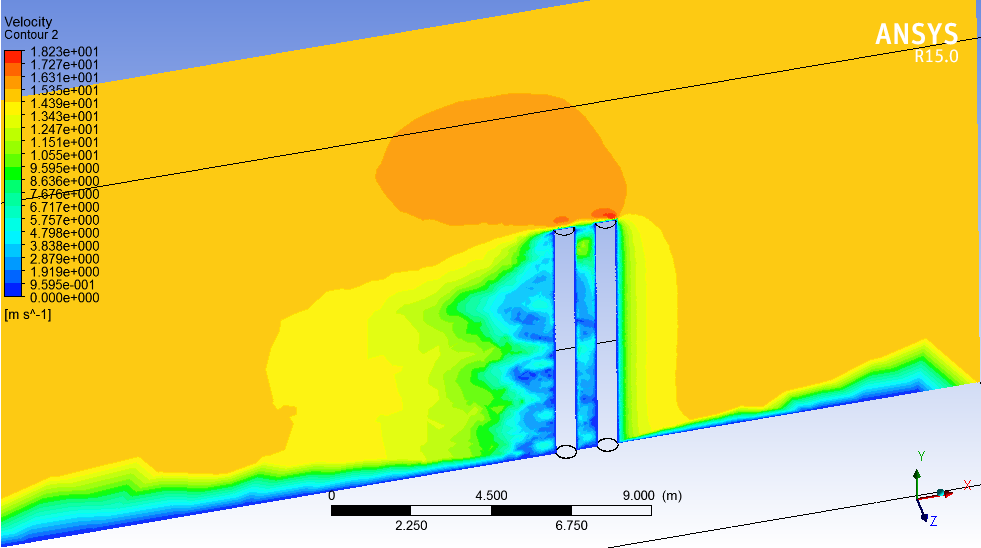
本论文应用ANSYS Workbench15.0中的Transient Structural模块和Fluid Flow（CFX）模块对L/D=2的串列双圆柱进行双向流固耦合数值模拟，得到了圆型双柱结构周围的速度流线图、不同截面的速度云图。通过理论计算风载荷的值与数值仿真值的对比，验证了模拟仿真的可靠性，并进一步得到上、下游圆柱顶点位移随风速变化的拟合函数。本文的研究成果对于研究工程实际中其他绕流问题有一定的参考价值。

关键词：圆柱绕流；流固耦合；圆型双柱结构；数值模拟

Abstract

The application of flow around cylinders is very extensive and has important engineering application background in practical engineering. Such as water flow effects on piers, offshore drilling platform pillars, pile foundation wharfs, and wind effects on chimneys, cylindrical buildings, and high voltage transmission lines. Circular double-column structure is a common structure in the phenomenon of flow around a cylinder, and its application in industrial engineering is also very extensive.

In this dissertation, the Transient Structural module and the Fluid Flow (CFX) module in ANSYS Workbench 15.0 are used to perform bi-directional fluid-solid coupling numerical simulation on two cylinders in tandem arrangement with L/D=2. And this numerical simulation obtained the velocity streamline diagram around the circular double-column structure and the velocity cloud diagrams of different cross-sections. Through the theoretical calculation of the wind load value and the numerical simulation value, the reliability of the simulation is verified. And further get the fitting function of upstream and downstream cylinders apex displacement with the change of wind speed. The research results of this paper have certain reference value for the study of other flow problems in engineering practice.

Key Words：Flow around cylinder；Fluid-structure interaction；Circular double-column structure；Numerical Simulation

目录

第1章 绪论 1

1.1 课题研究背景 1

1.2 国内外研究现状 3

1.2.1 固定支撑串列双柱 3

1.2.2 弹性支承串列双柱 4

1.2.3 涡激振动的主要特征 4

1.2.4 圆柱绕流的数值模拟方法 5

1.3 本文的主要研究内容 5

第2章 圆柱绕流 7

2.1 雷诺数和雷诺数效应 7

2.2 不同雷诺数下的单圆柱绕流特性 8

2.3 不同间距比下双圆柱绕流特性 9

第3章 串列双圆柱的数值模拟 10

3.1 模型建立及计算 10

3.1.1 模型参数 10

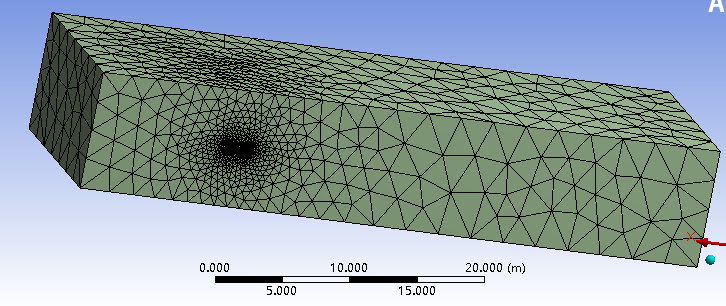
3.1.2 网格划分 11

3.1.3 Ansys仿真计算 12

3.2 模拟结果分析 13

3.2.1 流体的运动特性 13

3.2.2 圆柱的受力情况 15

3.2.3 风载荷计算 17

3.2.4 位移分析 20

3.3 本章小节 21

第4章 环境影响与经济分析 22

4.1 环境影响分析 22

4.2 经济性分析 22

第5章 总结与展望 23

5.1 总结 23

5.2 展望 23

参考文献 24

致谢 26

绪论

课题研究背景

大多数工程结构以阵列形式出现，如烟囱组，热交换器中的管道，架空电力线束，桥墩，化学反应塔和海上平台等，由流体流动引起的这些结构的振动减少了相应装置的使用寿命，因此在结构的设计中必须考虑到流致振动。在尾流附近涡流的交替脱落导致结构上的波动力，波动力与弹性结构之间的非线性耦合可能导致结构振动，声学噪声或共振。由于结构之间的相互作用，阵列中结构周围的流体动力学更为复杂。

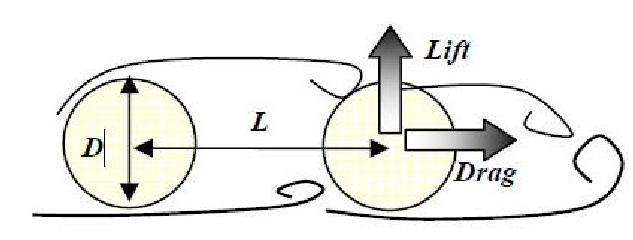串联双柱可以被选作最简单的情况，与上游圆柱分开的自由剪切层可以重新附着在下游圆柱上，并且两个圆柱间的流体具有不同的流动结构，如图1.1所示。剪切层的相互作用引起两个圆柱的振动，这可能会损坏结构，这些振动分为多种类型，对这些现象的详细检查和理解是重要的。其中一种是尾流诱发的振动，即尾流驰振，众所周知，它在圆柱响应振幅中涉及强烈的非线性。尾流驰振主要发生在具有特殊和非对称横截面的柔性、轻阻尼结构中。尽管圆柱体由于轴对称结构而产生振动，但当圆柱与另一个圆柱相互作用时可能会产生尾流驰振。尾流驰振的振动是发散的、低频的和大振幅的。除了理论工作，许多实验研究了不同横截面的圆柱体的振动特征。对于两个圆柱体，已经进行了许多实验来研究速度和振幅，升力，阻力和涡流引起的振动之间的关系，但是两个串联圆柱体的驰振产生机理尚未阐明。复杂的气动弹性现象存在不同种类的振动，这里将解释一些主要的气动弹性不稳定性。

图1-1 串列双柱

流体作用下结构的振动，按振动机理可分为抖振、驰振、颤振及涡激振动。

首先，涡激振动是一种经典的流激振动。它发生在斯特罗哈斯数St和来流速度U指定的流速范围内，来自上游圆柱的两个剪切层在下游圆柱上稳定地重新连接。间隙中的涡旋频率可以等于下游圆柱的固有频率，并且两个圆柱都会产生周期性的卡门涡旋，因此，两个圆柱都会振动。

其次，弛振是自激振动，在该自激振动中，结构的运动在相位上引起升力，并且依赖于横向于流动方向的结构的速度。弛振主要发生在具有特殊和非轴对称截面的柔性、轻阻尼结构中，如矩形截面或一些覆冰电力线电缆的有效截面。在卡门涡街中，弛振的振动频率往往比涡旋脱落频率低很多。

第三，从上游圆柱分离的两个剪切层重新附着在下游圆柱上；然而，其中一个分叉成两个，其中一部分在圆柱之间的间隙中滚动，导致不稳定的升力来激励上游圆柱。为了抑制尾流弛振，隔板、电缆横梁可以安装在电缆之间，如图1.2所示。尾流弛振的振幅是发散的，以致于许多装置由于尾流弛振而被强力破坏。两个上下游布置的柱体，只有在下游柱体的响应频率比它的涡脱频率及上游柱体的响应频率低时才有可能出现。在上游结构的尾流区存在一个不稳定驰振区，图1.3给出了这一不稳定区平均风速及下游结构上的阻力升力变化情况。尾流引起的弛振总是灾难性的，因此我们应该对其进行更深入的研究，以找到减弱弛振的方法。

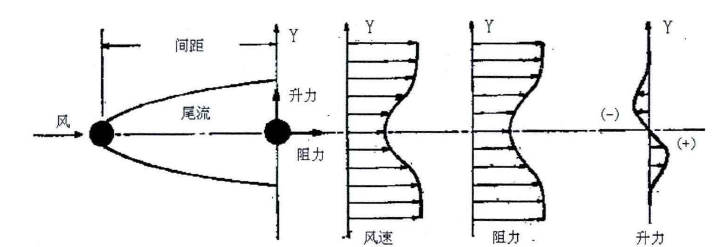图1.2 四束电力线图像中的间隔器

图1.3 上游柱体尾流中的下游柱体速度、升力及阻力分布示意图

国内外研究现状

固定支撑串列双柱

本文提到了串联布置的两个圆柱的数值研究，并在下面的讨论中介绍了其中的一些情况。流动特性取决于L/D和错位角，其中L是两个圆柱之间的中心到中心的距离，D是圆柱直径。对于串联布置的两个固定圆柱，有三个主要流型^[1]。接近状态，两个气缸表现为一个单体，L/D＝1～1.5，从上游圆柱分离的自由剪切层超过下游；重新附着状态，由上游圆柱发出的剪切层重新附着在下游圆柱上，在下游圆柱后面形成一个单一尾流，L / D = 1.5〜4，这由Alam.M.M ^[2,3]研究，在L/D＝3.5的串联布置的情况下，在Re＝10²时，上游圆柱没有形成涡流，而是在Re＝10³时观察到涡流。RioSHIKA^[4]认为雷诺数对流动结构与L/D之间的关系有影响。Alam等^[5,6]进一步将再附着体系分为两部分：交替附着剪切层（L / D lt;4）和稳定附着剪切层（3 lt;L / D lt;4）。交替重新附着的状态对应于较高的波动升力系数C_L，其中F_L是每单位的升力，ρ是流体的密度，并且U_∞是自由流的速度，而稳定重新附着的状态对应于两个圆柱上的较低的升力。在上游圆柱和下游圆柱后面分别观察到两个涡街的共脱落方式（L / Dgt; 4）。Zhou和Yi^[7]研究了每个区域内两个刚性串联圆柱体的尾迹，发现圆柱体的流体诱导振动与升力系数CL_f有关。图1.4显示了L / D = 1.1〜5.0的串联布置的两个刚性圆柱的CL_f分布，包括重新附着（L / D lt;4）和共同流出（L / Dgt; 4）方式。Bokaian ^[8]发现，当L / D = 4时，CL_f从较低的幅度跳到较高的幅度，L / D = 4被认为是临界值。

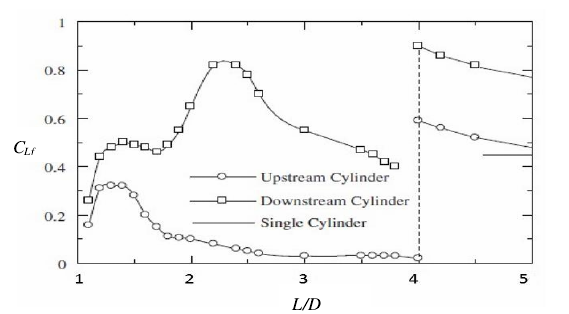
图1.4 随着L / D的变化，串列双柱升力系数CL_f的波动变化^[9]

弹性支承串列双柱

当一个圆柱在另一个固定圆柱后振动时，尾流和振荡圆柱之间的相互作用变得复杂，并且一些相关文献报道如下。Bokaian和Geoola ^[10]考虑了固定上游圆柱和弹性支撑下游圆柱的情况。在他们的实验中，根据圆柱距离和结构阻尼，圆柱呈现涡流共振，或弛振，或组合涡流共振和弛振，或分离的涡流共振和弛振，观察到弛振幅度对圆柱的纵横比敏感，当L / Dgt; 4时，单独发生涡旋共振。在其它试验中，在雷诺数较大的情况下，L/D＜8的弛振随着涡激振动的恢复而减小，这是由Brik＆LaNeViel^[11]研究的。Tokoro等^[12]研究了采用全气动弹性双柱模型的尾流弛振，这里使用的双柱布置的特征在于L/D比从5.3到9.7变化，即对应于“尾流弛振”的临界条件和由Gu和Sun^[13]命名的所谓“尾流引起的颤振”的值。当L/D＝5.3时，观察到典型的尾流弛振；在L/D＞7.5的情况下，该模型是稳定的。Strykowski ^[14]发现，摆动体后面的尾迹观察表明，在小振幅弛振运动期间，涡脱频率表现如同圆柱体静止一样。

涡激振动的主要特征

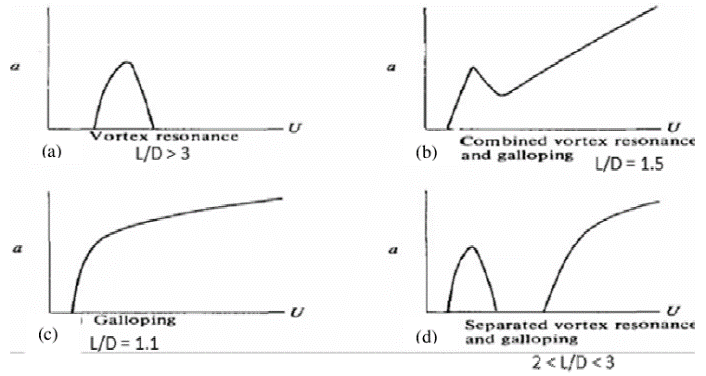所有相关文献得出的一个重要结论是在振幅和频率上，尾流引起的弛振完全不同于孤立的非圆形柱体的弛振。Kim，H ^[15]发现了孤立的非圆形圆柱体与尾流引起的弛振之间的两个重要区别。（1）弛振振幅和频率基本上不受自由流湍流强度有限增加的影响；（2）振动总是从平衡位置积聚（圆柱处于流体中）。振动开始，涡旋脱落频率略低于系统的固有频率fn，在增加流速时，漩涡脱落频率fv的值也增加并且等于fn的值，以降低的速度等于涡旋共振速度U_r。Hover，F.S.和Triantafyllou，M.S ^[16]认为在涡激共振的最后fv略高于系统的固有频率；Mahir，N^[17]认为在尾流弛振期间，随着流速的增加，脱落频率不断增加。最重要的是，在尾流中可能会诱发弛振的fv大于固有频率。图1.5显示了下游圆柱的不同响应：图1.5（a）表示指涡旋锁定，而（b），（c）和（d）分别表示尾流弛振，组合涡流共振和弛振以及分离的涡旋共振和弛振。

图1.5 下游圆柱响应的类型

从图中可以推断，圆柱的振动类型很大程度上取决于L / D，而且，在尾流引起的不稳定性中，在给定的L / D处对于不同的质量和结构阻尼，可以有多种模式。

圆柱绕流的数值模拟方法

随着计算流体力学理论的日趋完善与人工智能技术的迅速发展，目前可通过CFD数值模拟进行圆柱绕流的仿真分析。依据紊流模型选取的差异，圆柱绕流CFD数值模拟类型主要可分为四类：DNS直接数值模拟、LES大涡模拟、RANS雷诺时均法以及DVM离散涡方法。如表1-1所示，四种方法各有其优势和缺陷，在保证计算精度的前提下如何提高计算效率是在选择使用哪种方法进行数值模拟的重要问题。

确定了选择哪种紊流模型之后，CFD数值模拟的方法还需考虑另外一个不能忽视的问题—网格的生成。对于复杂的流体分离现象的流场计算，网格质量的优异在很大程度上决定了计算结果的可靠性和精确度，不合格的网格划分甚至还会在计算中导致不收敛的结果出现。此外，结构在流场作用下的振动一定会导致流场边界的不断变化，当流场边界的变化大到一定程度时就会使得网格畸形，进一步干扰数值模拟的正常运算。目前普遍选取的动边界的处理方法是ALE——任意拉格朗-欧拉方法。此方法同时具有欧拉方法以及拉格朗日方法两者的优点：首先在处理流固耦合边界的运动时它具有拉格朗日方法的优势，能够精确地捕捉流固耦合边界在流场作用下的变化；其次在处理内部网格时它具有欧拉方法的特点，即使内部的网格单元不随结构的振动而变化，独立于结构实体，但是此方法和欧拉方法又有些差异，通过在仿真计算过程中一定程度上调整此方法的网格位置，可以使网格单元不会出现影响计算正常运行的畸变。由此在计算大变形情况下的模型时选择任意拉格朗-欧拉方法是十分明智的选择。

本文的主要研究内容

根据研究内容，本文划分为五个章节，具体如下：

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：