英语原文共 4 页，剩余内容已隐藏，支付完成后下载完整资料

提高浮筏系统隔振特性的优化设计

张卫英，Mesbahi E

1. 大连海洋大学，海洋工程学院，中国大连116023
2. 纽卡斯尔大学，海洋科学与技术学院，英国NE1 7RU

zwy@dlou.edu.cn

摘要：浮筏系统越来越多的应用于船舶动力装置中以达到降低振动和噪声的目的；浮筏系统是多台设备安装在同一隔振系统，并且其隔振系统含有双层隔振器和中间筏架。浮筏系统的优化设计对提高设计水平和提高隔振性能有着重要的意义。本文主要是建立了浮筏系统的有限元模型，并对其系统模型进行了一些计算，再通过直接有限元法分析确定其振动特性。此外，本文为提高浮筏系统的隔振性能构思了一些优化模型，以中间筏架的局部厚度为设计变量，通过控制中间筏架的重量，观察浮筏系统的加速度，采用可行方向法求解其优化方法。本文实现了一个实例优化，通过优化结果表明，在不增加重量的同时，中间筏板厚度的重新分配对隔振性能有较大的提高。
关键词：浮筏；隔振；有限元法；优化设计

1. 介绍

船舶振动主要来源于机房的动力机械，特别是发电机组和辅助设备的振动。振动控制的目标是减少振动的幅度，并使振动源隔离。良好的措施能有效地减少其对周围环境的传播，减少振动和噪声的总等级。随着船舶性能要求的提高，越来越多的浮筏系统（FRS）被用来阻断从主机到船体的振动传播，以达到降低振动和噪声的目的^[1]。浮筏系统是多台设备安装在同一个隔离系统上的一个装置，它包括两层隔振器和一个中间浮筏。实际应用证明，浮筏系统可以有效减少传向船体的振动^[2]。浮筏系统的优化设计可以大大提高整个系统的隔振性能。许多研究人员都参与了这一领域的研究。王宇等人^[3]基于双层隔振系统建立了一个二次频率响应函数，基于可以降低振动水平的目标函数建立了一个数学优化模型，且以筏架的刚度系数、材料参数和厚度作为设计变量，用差分方法计算目标函数的灵敏度和频率响应，实现了隔振器的优化设计目标。X.CHEN等人^[4]基于总参数模型得出了双层隔振系统的振动传递和模态频率曲线，并以模态阻尼比、频率和系统的质量为设计变量，使用最大熵的方法处理设计变量的问题和实现了系统参数的优化。郑学贵^[5]分析和计算了浮筏系统对自然频率的敏感性、浮筏材料的密度和质量，并在上述研究结果的基础上更新了系统参数，提升了隔离系统的动态特性，改进了隔离系统的隔振效果。

本文对浮筏隔振系统进行了研究，通过建立浮筏系统的有限元模型，利用有限元（研究复杂浮筏系统的基本方法）来计算隔振特性和振动反馈。并建立了一个优化模型，其优化目标是最大限度地减少隔振系统中弹性基础的加速度响应，以筏架的局部厚度为设计变量，采用可行方向法来优化设计变量，实现宽频带筏帧厚度的优化分布。

1. 结构振动分析的有限元法

当附加模拟的动态负载时，浮筏结构的稳态有限元方程可表示如下：

（-w²[M] [K]){U}={F} （1）

如果[M]、[K]分别是结构的质量矩阵和刚度矩阵，w是激振角频率，{F}、{U}分别是激振载荷幅值向量和位移幅值向量。通过求解方程（1），可以得到振动的结果，包括位移、速度和加速度。如果载荷幅值向量{F}=0，那么可以从方程（1）中计算得出结构模态。

1. 模型和算法的优化

浮筏系统的优化设计是为了减少传向基座的振动，即减少发动机振动和由其产生的基座振动。如果可以使连接下层振动器与基座之间那个地方的垂直振动加速度最小化，那么传向基座的振动也可以降低，因此可以建立如下所示的数学模型：

设计变量

X=（x₁,x₂,hellip;,x_i,hellip;,x_n) （2）

目标函数：

（3）

约束条件：

G(X）le;G₀

x_d＜x_i＜x_u,i=1,2,L,n （4）

其中X={x₁,x₂,L,x_i,L,x_n}^T为设计变量向量，x_i为第i个变量，n为设计变量的数量；y为目标函数；m优化频率的数量；h为优化节点的数量，即为筏架和下层隔振器连接点的数目，也就是下层隔振器的数目。U_i,j为第i个节点频率为j时的响应加速度，G是中间筏架的质量，G₀是筏架的初始质量，G(X）le;G₀是约束条件，x_d和x_u分别是设计变量的上限和下限。

前面提到的模型是一个典型的约束优化问题。利用可行方向法优化设计变量，这是一个迭代过程，即根据一系列可行的方向，找到最佳的解决方案。所谓的可行方向S被定义为从一个可行点x^(k)指向另一个可行点x^{(k 1)}的矢量方向，迭代公式为x^{(k 1)}=alpha;S^（k) x^(k),其中alpha;为迭代空间，可行方向法可由以下两步实现：

首先是确定一个可行的方向，其次是找到迭代的空间alpha;，此时可沿着可行方向S和迭代空间alpha;确定一个新的点x¹。其中有两个条件会使迭代终止，一是连续两次迭代的目标函数的变化值小于一个给定的数值，称为规则收敛，另一个是连续两次迭代的设计变量的变化值小于一个给定的数值，称之为软收敛。当迭代满足以上两个条件之一时，迭代停止，这个现象可以称之为收敛的优化设计。

1. 有限元模型和频率响应
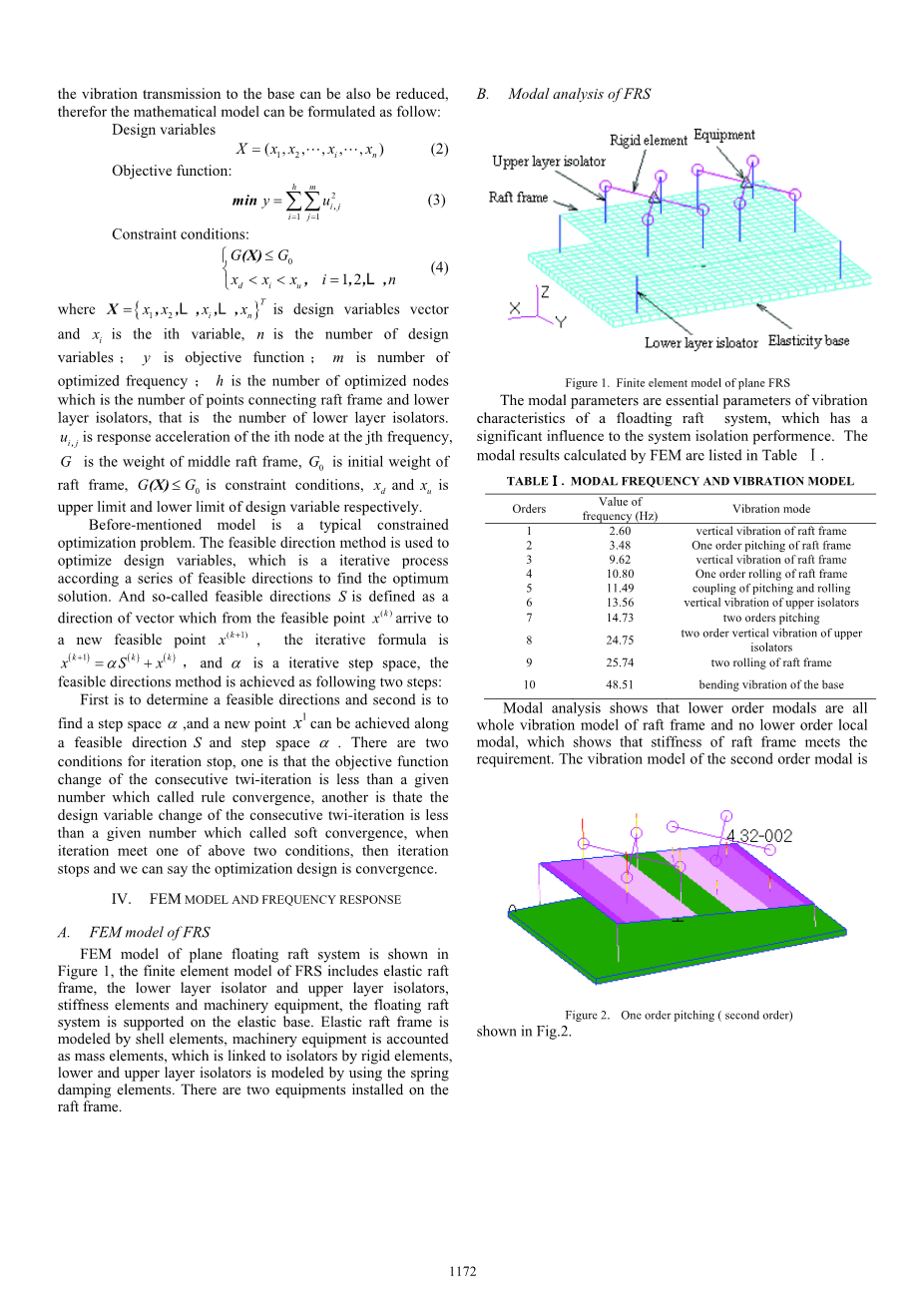
2. 浮筏系统的有限元模型

平面浮筏系统的有限元模型如图1所示，浮筏系统的有限元模型包括弹性筏架，下层和上层隔离器隔离器，刚度元素和机械设备，而浮筏系统是由弹性基座支撑的。弹性筏架是由一个壳单元模拟的，而机械设备作为质量元素放置在上面，它是通过弹性阻尼元件模拟的刚性元件、下层隔振器和上层隔振器与筏架连接的。筏架上安装了两台设备。

1. 浮筏系统的模型分析

图1 平面浮筏系统的有限元模型

模态参数是浮筏系统的振动特性的一个重要参数，它对隔振系统的性能有重要的影响。用有限元法计算的模拟结果如表Ⅰ所示。

表Ⅰ 模拟频率和振动模型

模态分析表明，低阶模态是筏架全振动模型和无低阶局部模态，这表明筏架刚度满足要求。振动模型 的二阶模型如图2所示。

图2 一阶上下振动（二阶）

1. 浮筏系统的频率响应分析

浮筏系统是在机械设备的动态载荷作用下工作。但一般而言，浮筏系统上安装的机械设备的激振频率较高，在激振频率较高时，隔振系统具有较好的隔振性能，而且激振频率越高，浮筏隔振系统的性能越好。因此，中间频段的有效隔振性将决定隔离系统的性能。为了在频带区域内分析和优化隔离系统写的效果，对每个机械设备施加垂直方向向下一个激振力，频率范围从1Hz到1000Hz，激振力为每10N一级，这是用来模拟机械运转的有效激振。分析结果表明，当频率低于300Hz时，基座的弹性振动较大，这说明了低频段的隔振性能较差。但实际的加工机械的激振频率一般在300Hz以上，且随着频率的升高，基座的弹性振动会降低。当频率在400Hz-800Hz时，下层隔振器与基座之间连接点的加速度响应曲线如下图3所示。可以发现有四个点的加速度是相同的，这是因为弹性基座上四个隔振器是对称分布的。从图3可以看出两个频带分别对应两个峰值，其中一个频带是从400Hz到450Hz,另一个是从700Hz到760Hz。当频率高于800Hz时，振动加速度低于10^-7m/s²。因此，在这两个频带重中通过优化来减轻基座的弹性振动，对提高浮筏隔振系统的性能有着重要的意义。

图3 基座的加速度响应曲线

1. 浮筏系统的优化
2. 设计变量

在不增加整个系统重量的前提下，为了提高隔振系统的隔振性能，可对中间筏架重量的重新分配进行优化处理。将中间筏架划分为15部分，将每个部分的厚度作为设计变量，如下图4所示。图4表示筏架的整个面积。a,b,c,d这四点代表下层隔振器与弹性基座之间的连接位置，e,f,g,h这四点代表上层隔振器与一台设备之间的连接位置，k,l,m,n这四点代表与其他设备连接的位置。每个部分的厚度作为设计变量分别用1,2,3，hellip;，14和15标注。

图4 筏架上设计变量的划分

1. 实际优化模型

根据图3所示的加速度响应曲线，有两个峰对应的两个窄频带的频率分别为450HZ到550Hz和 700Hz到760Hz，所以对目标函数优化主要是为了降低峰值。根据公式（2），（3）和（4）可知，在这两个频段减少基座振动的数学模型可建立如下所示：

设计变量：

X=(x₁,x₂,hellip;，x_i,hellip;,x₁₅) (5)

目标函数：

（6a）

（6b）

约束条件：

G(X）le;231.66kg

0.02＜x_i＜0.05,i=1,2,L,15 (7)

上述数学模型表明：设计变量的数目为15，分别用x₁到x₁₅表示。有两个目标函数，一个需优化的频率数目为50（从450Hz到550Hz，以2Hz为一个频率间隔），以公式（6a）命名；另一个需优化的频率数目为30（从700Hz到760Hz，以2Hz为一个频率间隔），以公式（6b）命名，因此，需要优化的频率数目分别为30和50。初始筏架的重量不超过231.66kg，设计变量的变化范围在0.02m到0.05m之间。

1. 优化结果的分析

   剩余内容已隐藏，支付完成后下载完整资料

   ---

   资料编号：[146891]，资料为PDF文档或Word文档，PDF文档可免费转换为Word