英语原文共 14 页，剩余内容已隐藏，支付完成后下载完整资料

用于数控车床3D曲面加工的CAM系统开发

（第一篇）

摘要

我们开发出一种新的加工方法，该方法实现了非对称旋转曲面轴的加工（下文称为NACS-车削）。 NACS-车削是由一个转动轴和两个平行轴，3轴同步的数控车削方法。该方法采用在X轴安装马达，并通过高速旋转X轴同步形成一个非对称旋转曲面的轮廓。我们使用该加工方法时，生产率得到显著提高。目前NACS-车削的一个应用是刀具路径设计，主要通过商用3D-CAD程序和几何计算相关的API获得。因此，在本文中我们讨论已经应用的NACS-车削的一个新的CAM应用。因为这种加工方法是三轴同步控制，虽然轴的组合与一般的两轴车床相同，但刀具路径在三维空间中产生。因此，采用加工中心的刀具生成方法是必需的。具体来说，通过计算作为计算机加工的自由表面，以及使用逆偏移法计算工件中心点坐标相交线上产生加工点。在本文中，首先介绍NACS-车削的轮廓表示方法。接着，最后以旋转刀具为例具体分析CAM系统的细节。最后，我们通过切割实验验证论文内容的有效性。

关键字： CAM，三维加工，车削，非轴对称面，旋转刀具

1.绪论

目前，非圆截面形状的零件，如凸轮轴轮廓或活塞内燃机一般是通过切割或使用专用的加工工具磨削加工（Yoneda等人，1990）（Mi-Ching和Yaw-Hwei，1999）。由于出现了需要旋转轴加工机器的各种机械部件，不仅有常见的是使用专用加工工具，而且还普遍使用多用途机床构成的非轴对称三维表面。然而，在这种情况下，非圆形状通过铣削加工。这意味着，一个车削主轴用于索引轴。因此，如果我们需要获得特定的表面粗糙度，加工时间肯定会相应的增加。

为了解决这个问题，非回转轴曲面车削加工（下文称为“NACS-车削”）在我们的研究中得到应用（Morimoto等人，2012a，2012b）。在NACS-车削中，X轴驱动用的高速线性电动机在Z轴方向不断地供给。这使得非圆形加工与转动主轴的旋转同步。我们已经证实，在X轴可通过4.5G的最大加速度进行驱动并可以按照750 rpm的主轴转速旋转一周。

因此，NACS-车削说明了硬件系统具有足够的加工能力来创建曲面。然而并没有支持此专门加工方法的CAM应用。在这一方面，市场上销售的三维CAD程序刀具路径设计多使用几何计算得到，缺乏相关的通用性API来支持。因此，本文提出了NACS-车削，它是一个新的多功能刀具轨迹生成方法。这种加工方法需要在三维空间中给定这两个平行轴和旋转主轴从而同步它们的运动，这不同于一般车削控制生成的刀具路径。

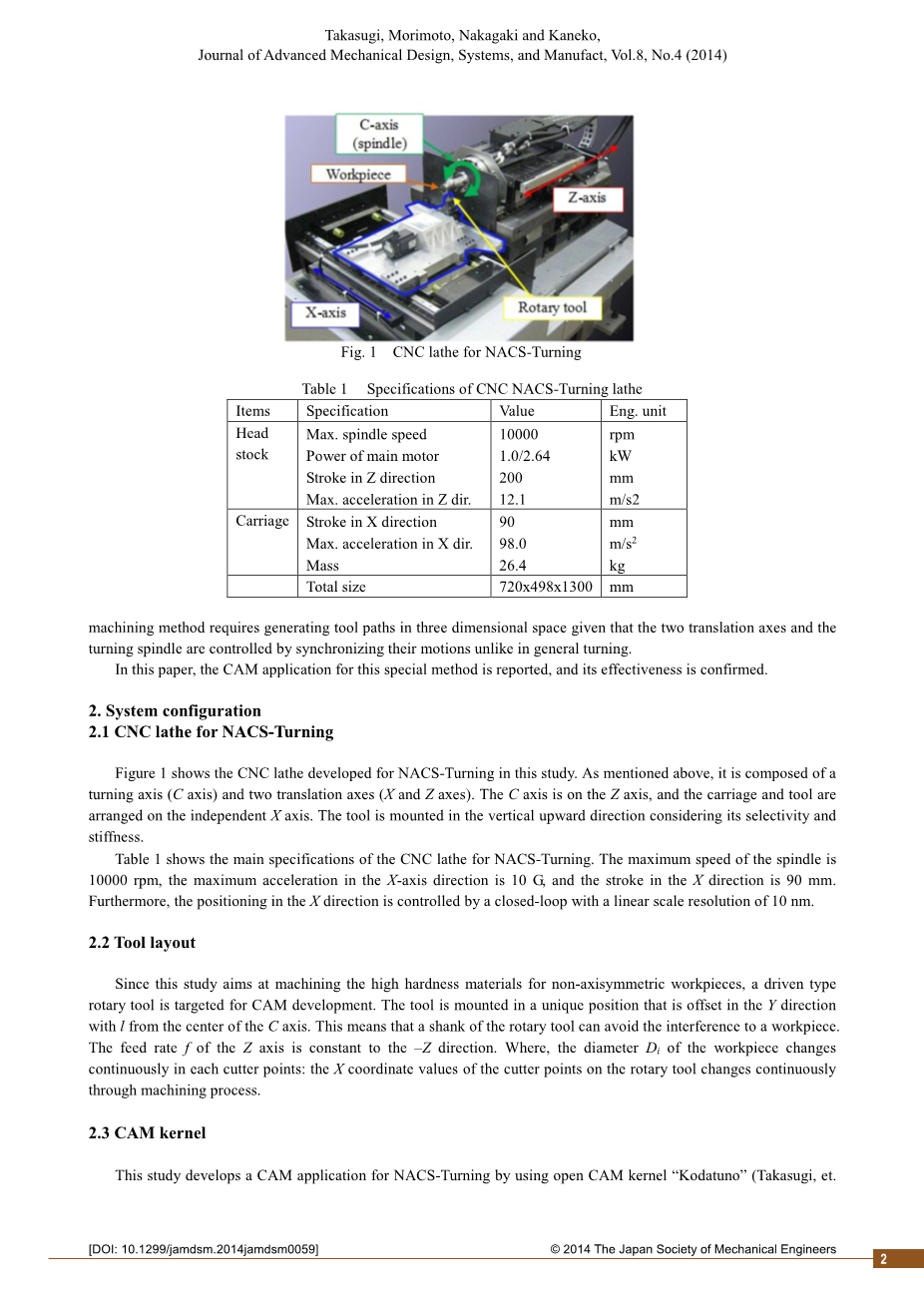
图一：数控车床NACS-车削

表一 CNC NACS-旋转设备的规格

在本文中，对于这种特殊方法的CAM应用，其有效性得到了确认。

2.系统配置

2.1数控车床NACS-车削

图1表示出了用于NACS-车削及研究开发的数控车床。与上文提到相同，它是由一个旋转轴（C轴）和两个平移轴（X轴和Z轴）组成的。 C轴是在Z轴上，并且托架和工具被独立的布置在X轴上。该工具被安装在垂直向上的方向，需要考虑其选择性和刚度。

表1列出了数控车床NACS-车削的主要规格。主轴的最大速度是10000rpm，在X轴方向上的最大加速度为10g，并且在X方向上的行程为90毫米。此外，在X方向上的定位是通过一个闭环10nm分辨率的线性标尺进行控制的。

2.2工具布局

由于本研究的目的是用于加工非轴对称工件，其材料硬度高，从动型旋转工具是针对CAM的发展而设计的。该工具安装在一个独特的位置，即Y方向上与L-从动C轴由一定的中心偏移。这意味着，在旋转工具的柄部可避免工件的干扰。控制进给速率f的Z轴是恒定的-Z方向。在这个方向，每把刀具点工件变化的直径Di是连续的，X坐标上的旋转工具切割点的值在机械加工过程中不断变化。

2.3内核CAM

图2工具布局

图3刀位轨迹生成方法图 图4刀具中心轨迹与逆偏移方法

本研究通过使用开放CAM内核“Kodatuno”发展为NACS-转动CAM应用（Takasugi等，2011），而不是为一般3D CAD的API。 Kodatuno是一种表面开源的内核，这已经由金泽大学第一作者提出。所有输入的3D模型转换为NURBS（不均匀有理数B样条），从而进行表达和保留。通过这样的结构，它推导出均匀几何计算的整个CAM应用。另外，由于我们可以直接使用NURBS进行表示，与一般CAM应用开发和商业三维CAD应用开发进行比较，冗余和误差可降低到最小。

3.刀具路径生成方法

通常，刀具轨迹生成曲线要在刀具半径方向补偿一个球头立铣刀半径大小的尺寸，球头铣刀中心点的位置就是加工过程中采用的工具路径。在这种情况下，刀具轨迹生成方法分为以下两种类型。

（1）生成与刀具半径预先偏移的表面，并产生参照表面上的工具路径。

（2）原表面上生成点，以及刀具半径法线方向抵消的这些点。该方法与（1）比较，有一个缺点，法线方向抵消了这些点，即它难以保持足够的精度，因为包络面内插有近似的操作表面。然而，它可以很容易按规则的间距生成各数据点的路径。另一方面，而方法（2）不需要为工具中心点代入近似计算，这样也会有一个缺点，即抵消点将产生不规则间距。

在该加工方法中，由于C轴和进给运动的旋转必须同步，这是初始条件，这时对于刀具路径上的点在Z方向上间距一定。此外，如图3所示，如果每转控制点的数目是固定的，由于每个控制点之间的角度间距Delta;theta;是恒定（2pi;/ n）时，连接到所述的Z方向，需要产生在每个旋转角点内插的曲线：它不需要考虑插值表面。因此，本研究采用方法（1）。

以下章节描述在NACS-车削刀具轨迹生成的三个过程。

3.1工具中心点的层次

如图4所示，用于生成工具中心点轨迹的逆偏移法（Kondo等人，1988）。具体流程被分为下列五个方面。

（1）旋转角度theta;，其对应于上平面的旋转刀具和工件表面S上的平面P，以及两者之间的交叉点Q（Higashi，等人，1990）。其中，Q影响的计算间距delta;会产生一个近似误差，它将影响下一步中NURBS插补曲线的生成。

（2）在表面S上，计算法向量Q中的一般矢量N。

（3）向平面P上投影N向量

（4）刀具中心点的轨迹Q在旋转角theta;中的位置，由标准化刀具半径D / 2投影矢量投影得到的。

（5）在0到2pi;之间角度间距为Delta;theta;的旋转轴线上,计算每一个刀具中心点的轨迹。

3.2 NURBS插补曲线的产生

在每偏移theta;角度过程中，NURBS插补曲线从计算刀具中心轨迹点中产生。因为这种加工方法不涉及插值后的表面，近似误差的旋转方向取决于角间距Delta;theta;。另一方面，上面的部分作为所述的近似误差，它在Z方向的数值取决于内插点。封闭圆弧曲线的边缘增加，这时弧曲线就由NURBS方法表示出来了。

3.3刀具位置数据

利用每个偏移NURBS插补曲线以及平面R上具有z坐标刀位置和法线矢量的值，在Z方向进行计算每个加工点坐标的精确坐标。其中 z值定义如下：

其中 （1）

其中f是主轴每转进给速率，n是每转的分割数（偏移NURBS插补曲线的数量），以及L是切削进给方向的长度。C和R之间的交叉点的计算方法如下：

（2）

其中，Rn为R的标准矢量，p是在R上的点。如果式（2）的NURBS度数比小于4度，该公式可以用代数方法求解。但在本报告中，由牛顿法收敛法计算整体工作状况。

4.CAM系统的验证

为了验证开发的CAM系统在用于NACS-车削时的有效性，采集在加工过程中生成的CL数据和刀具路径精度数据。

4.1验证CL数据生成方法

表2 切削条件

图5 工件验证

图6刀具中心点的结果

图7 NURBS插补曲线的结果

图8刀具位置生成的结果

图5是用于验证的工件示意图。切削长度为21毫米。工件的直径从边缘面沿-Z方向逐渐扩大。圆的中心视轴的转动到 Y方向改变其方向。用于产生CL数据的必要切削条件如表2所示，每转的分割数为720，切割点的旋转角度间距Delta;theta;为0.50。从式（1）中，在Z方向切削点之间的距离被设定为2.78x10-4毫米。三种类型的交叉点计算参数delta;，并检查delta;改变后的影响。在此验证中，工作平台（采用的操作系统：Windows 7 64位CPU： 最高3.60 GH 8核，内存：16GB）

图9 X轴位置的变化（delta;1.0）

表3 各交叉点计算处理时间的比较

（a）delta;1.0的情况 （b）delta;0.5的情况 (c) delta;0.2的情况

（d）误差分布（delta;1.0 - delta; 0.2） （e）误差分布delta; 0.5 - delta; 0.2

图10计算间距delta;条件之间的误差分布差异

表4每个delta;之差的最大

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[148369]，资料为PDF文档或Word文档，PDF文档可免费转换为Word