超声振动加工用变幅杆的参数化设计系统开发毕业论文
2020-02-17 19:47:46
摘 要
超声变幅杆是超声振动系统中至关重要的一环。超声变幅杆的参数化将会极大程度上提高模型的设计和制造效率。其中变幅杆的主要参数有半波谐振长度、谐振频率、放大系数和位移节点长度等。本文主要包括以下研究内容:
1:对于指数型、圆锥形、悬链线形和阶梯形四种圆截面半波长谐振变幅杆进行参数设计计算和分析;
2:在ug12.0中分别构建指数型、圆锥形、悬链线形和阶梯形四种半波谐振变幅杆的基础模型;
3.在visual studio2010中进行参数化界面设计并且构建代码,建立与UG12.0之间的联系;
4.在之前建立的四个模型中进行测试,并且成功实现超声变幅杆的参数化。
通过超声变幅杆的参数化实现,方便了相关设计人员的模型建立,同时也能提高工厂的生产效率。
关键词:超声加工;变幅杆;参数化。
Abstract
Ultrasonic horn plays an indispensable role in ultrasonic vibration system. Parameterization of ultrasonic horn will greatly improve the design and manufacturing efficiency of the model. The main parameters of the horn are resonance frequency, half-wave resonance length, amplification factor and displacement node length. This paper mainly includes the following research contents:
1. Design, calculate and analyze the parameters of exponential type, conical type, catenary type and stepped type semi-wavelength resonant amplitude transformer with four circular sections;
2. In ug12.0, the basic models of exponential type, conical type, catenary linear type and stepped type half-wave resonant amplitude transformer are respectively constructed;
3. Parametric interface design and code construction in visual studio2010 to establish the connection with UG12.0;
4. Tested in the four models established previously, and successfully realized the parameterization of ultrasonic amplitude transformer.
The parameterization of ultrasonic horn facilitates the model building of relevant designers and improves the production efficiency of the factory.
Key Words:Ultrasonic machining; The amplitude; The parameterized.
目录
摘要 I
第1章 绪论 1
1.1引言 1
1.2国内外研究现状 1
第2章 超声加工概述 2
2.1超声加工的概念 2
2.2超声加工的原理 2
第3章 超声变幅杆的介绍与设计 3
3.1超声变幅杆的概述 3
3.2变截面杆总振动的波动方程 3
3.3指数型变幅杆 4
3.3.1频率方程和谐振长度 5
3.3.2位移节点 5
3.3.3放大系数 5
3.3.4形状因数 5
3.4悬链线形变幅杆 6
3.4.1.频率方程和谐振长度 7
3.4.2.位移节点 7
3.4.3放大系数 7
3.4.4形状因数 7
3.5.圆锥形变幅杆 8
3.5.1频率方程和谐振长度 8
3.5.2位移节点 9
3.5.3放大系数 9
3.5.4形状因数 9
3.6阶梯形变幅杆 10
3.6.1频率方程和谐振长度 10
3.6.2位移节点 10
3.6.3放大系数 11
3.6.4形状因数 11
第4章 超声变幅杆的参数化计算 12
4.1指数型变幅杆 12
4.2悬链线形变幅杆 12
4.3圆锥形变幅杆 13
4.4阶梯形变幅杆 13
第5章 超声变幅杆的建模及其参数化 15
5.1建模软件UG的概述 15
5.2UG的二次开发 15
5.3变幅杆建模 16
5.3.1指数形变幅杆 16
5.3.2悬链线形变幅杆 17
5.3.3圆锥形变幅杆 17
5.3.4阶梯形变幅杆 19
第6章 超声变幅杆的参数化 20
6.1软件visual studio介绍 20
6.2 VS2010和UG之间的环境配置 20
6.3变幅杆参数化界面构建 21
6.3.1.指数型变幅杆参数化界面 21
6.3.2悬链线形变幅杆参数化界面 30
6.3.3圆锥形变幅杆参数化界面 34
6.3.4阶梯形变幅杆参数化界面 38
总结与展望 44
参考文献 45
致谢 46
第1章 绪论
1.1引言
超声变幅杆,它的截面外形从左到右一般情况下都是处于连续变化当中。其作用是在超声振动系统里,不单能放大机械振动质点的位移量和速率,并且能将超声能量聚在一个很小的范围里,即为聚能作用[1]。此外,它还可以起到阻抗匹配的作用,即连接换能器和负载,让能量传输更加的高效。
参数化指的是将一个工程或者模型编写为函数的形式,操作者只需要在参数化界面中输入几个简单的数据,就能得到工程的结果或者所需要的模型。这就是设计的自动化过程,极大提高了设计的效率并降低了上手的门槛,使更多人能够胜任这份工作。这也是在设计行业所趋向的一个新的形式。
而本文所做的就是将超声变幅杆和参数化结合起来,针对于这方面,对变幅杆的四种类,即指数型、悬链线形、圆锥形和阶梯形型进行新的研究和尝试,争取建立一套完整的超声变幅杆的参数化系统。
1.2国内外研究现状
对于超声加工,人们认识已久。从1927年美国物理学家伍德和卢米斯开始做的超声加工实验至今,超声加工已经广泛运用到工业领域当中。超声振动切削技术能帮助研制新的刀具材料,从而进一步提高被加工材料的精度;超声复合技术给人们带来有关绿色制造崭新的方向,能有效避免因使用工作液体导致的各种环境污染问题;应用于精密加工车床上的超精密加工技术中也涉及到了超声加工,并且还大量用于航空航天和国防当中。
随着科技的进步,超声加工凭着加工范围广、加工精度高、操作方便快捷、对车床结构要求简单等特点已经与工业和制造业紧密结合起来。而在超声加工系统中扮演关键先生的超声变幅杆,也吸引了许多人的关注和探索。
罗澜,凤飞龙等人基于圆柱中的导波模式解提出了精确求解大尺寸阶梯变幅杆振动频率与振动模态的解析计算方法,但是并没有继续深入应用到参数化中[2];马继召,祝锡晶等人以圆锥形变幅杆为例对变幅杆进行参数化设计,但仍有一定的局限性[3];李彬,李亚等人在圆锥过渡阶梯型复合变幅杆的优化设计中,用ANSYS进行优化,并通过APDL语言对变幅杆进行参数化建模和模态分析,通过编写的程序代码,VB可视化调用ANSYS生成的优化文件,实现了变幅杆的参数化优化设计,但是过程有一定的复杂性[4];王忠进,缪兴华等人采用解析法设计了阶梯形超声变幅杆,并采用有限元分析法制作变幅杆并对其修正和仿真,但是不方便进行参数化建模[5];吕升锋,龙建军等人运用ANSYS Workbench软件,设计带有加工工具的超声变幅杆并进行模态分析,并在此基础上优化设计,设计带加工工具的阶梯形超声变幅杆提供了新思路,但仍存在不能统一参数化建模的不足之处[6]。
本文只是在众多前者的成果基础上,进行对于超声变幅杆的参数化研究。
第2章 超声加工概述
2.1超声加工的概念
通常,声波的频率只要在20KHz以上的就被称为超声波。值得注意的是,超声波的上限是1014Hz。虽然人们感觉不出它的存在,但是我们却可以巧妙的利用它。
超声波具有空化效应。在液体中因为涡流或超声波等物理作用,致使有的部分形成局部的临时负压区,从而引发液体或液-固体界面的断裂,构成细小的空泡或气泡。这些空泡或者气泡并不是稳定的状态,有初生、发育和迅速闭合的几个过程。当它们迅速闭合时,会引发一微激波,从而导致局部产生很大的压强。这种气泡在液体中形成和随后迅速闭合破灭的现象被叫做空化。而伴随着超声波的空化效应,所形成的非线性振动能够产生一个爆破压力,进而导致破坏工件,当然,只要使用得当,便能够利用这点进行加工。
超声波是机械波,可以在三态中传播。只是在不同的环境中传播的波形和速度不同。比如,纵波、横波、表面波、板波等等,而对于不同的波形,都有相对应的速度公式和加速度公式。这些性质在超声技术中起到关键性的作用。
超声波遵守叠加的规律,但是叠加其实不影响各自的原有特性。可是如果是两个具备相同频率、固定相位差的声波叠加时,会出现干涉现象,从而引发部分声场空间加强或者减弱,这被称作干涉现象。超声波的衍射指的是媒质中的波动传到的每个点,都可以当作是发射声波的新波源。实际上,当测量过程中被测材料有两个相互平行且与波的传播方向垂直的表面,波会在这中间发生多次反射,导致在某些特定点上振幅可以达到非常大或者非常小接近于零。这时候称作共振状态。
另外,超声波还具有吸收的特性,这能帮助探索介质的特性和结构;其所具有的多普勒效应能帮助测量速度等。作为一种超声振动的工具,也作为一项新兴加工的特种加工技术,引起了国内外学术界人士的关注,也渐渐成为机械行业一个加工的新版图。
2.2超声加工的原理
超声加工的原理主要是先将超声波所产生的振动放大,产生的能量推动工具头做纵向的振动。这时候工具头就会将冲击力传递给磨料,而磨料又会进一步冲击给我们所加工的工件表面,这样就能使工件表面变形成我们想要的形成。这就是加工的原理。
另外,除了上述的通过分散的磨料来碎除材料的加工方式,还存在其他超声加工方法,比如和车刀的车削加工结合实现深小孔加工,亦或者帮助实现同种或者异种固体材料的焊接加工。
第3章 超声变幅杆的介绍与设计
3.1超声变幅杆的概述
超声变幅杆主要功能是放大振动时的每个质点的位移量和运动速度从而使输出的振动幅度能达到实际应用的需求。变幅杆可以分为纵向振动变幅杆、弯曲振动变幅杆、扭转变幅杆。纵向振动变幅杆又可以分为简单形和复合性。本文主要针对简单形的纵向振动变幅杆进行研究,其可以分为指数型、圆锥形、阶梯形和悬链形。而至于复合型,主要是各种简单形的变幅杆根据实际进行叠加而成。
超声变幅杆的性能主要可以由一下几个参数衡量:共振频率,共振长度,放大系数,形状因数,输入力阻抗等等。放大系数Mp是指变幅杆工作在共振频率时输出端与输入端的质点位移或速度振幅的比值;形状因数φ是衡量变幅杆所能达到最大振动速度的指标之一,它仅与变幅杆的几何形状有关, φ值越大,所能达到的最大振动速度也越大;输入力阻抗Zi定义为输入端策动力与质点振动速度的复数比值。
3.2变截面杆总振动的波动方程
介质中的每个点之间都存在着弹性的联系,所以只要有任意一点振动,就会带动相邻的点依次振动,这样就能让振动在介质中传播出去。这种现象被称为波动。
我们先假定一个前提,假设变截面杆所构成的材料都是均匀,而且是同性的,当杆的横截面尺寸远小于波长时,就默认为平面纵波沿杆轴向传播,那么这时候在横截面上应力分布均匀。
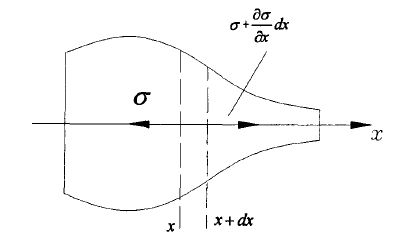
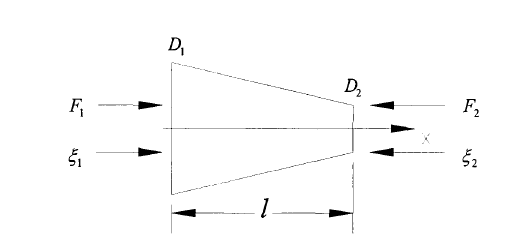
图1 变截面杆的纵振动
如图1所示,任意选一个变截面杆,假设其对称轴为X轴,这中间我们任选一个小的体积元。对于在X和X dx中的作用张力,再结合牛顿定律可以得出动力学方程:
其中,S为杆的横截面积系数;ξ为质点位移系数;σ为应力系数;ρ为杆材料的密度;
其中E为杨氏模量。
从而在谐振条件下,能够得出变截面杆的纵振动波动方程:
其中,k是圆波数,k=ѡ/c;w是圆频率;c是纵波在细棒中的传播速度,c。
下面本文的讨论均在这个公式上进行,包括讨论单一变幅杆中四种类型的计算,如谐振长度,形状因数,放大系数等。
3.3指数型变幅杆
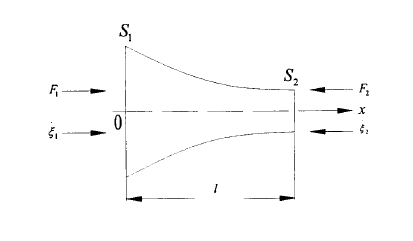
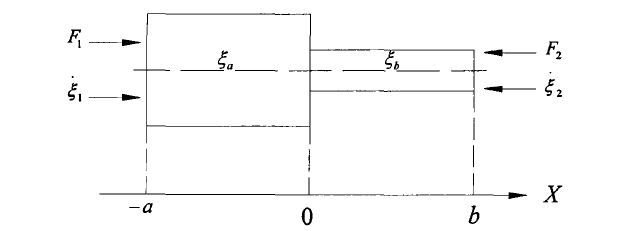
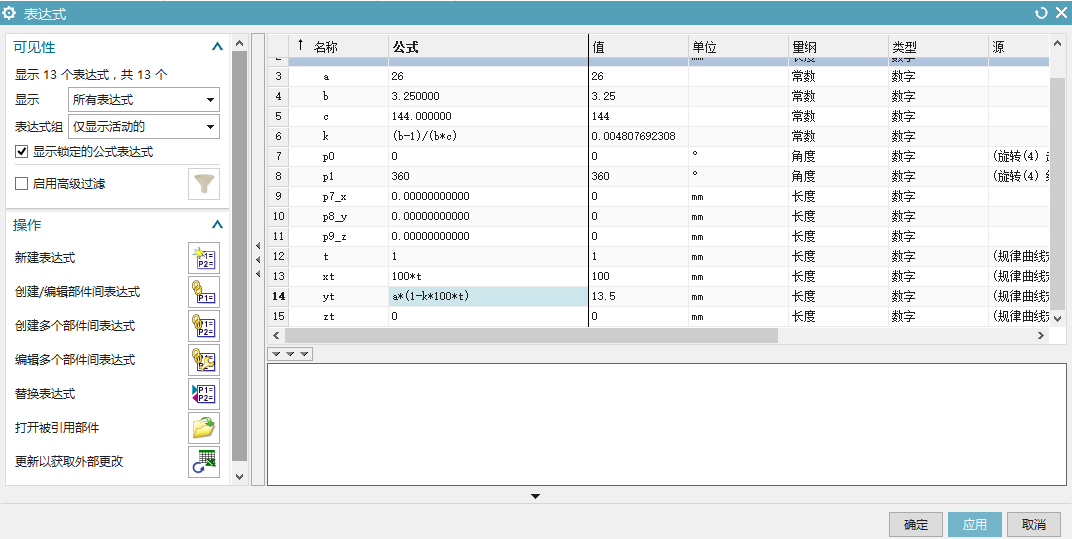
图2.指数型变幅杆
如图所示为指数型变幅杆,假设其左边中心所处于远点的位子,此处截面面积为S1,而X为L处的截面面积为S2,假设直径从D1到D2.那么形状参数及其截面积和X坐标的关系就是D=D1;S=S1。
其中β=;
面积系数N=(S1/S2)1/2=R1/R2;
代入到前面纵振动的波动方程,计算得出解为
ξ=
其中K’=(k2—β2)1/2。
当没有负载的时候,对其共振频率、放大系数、形状因数和位移节点等进行讨论。
3.3.1频率方程和谐振长度
由上文可得出关系式[1 (β/k’)2];
从而推出sin k’l=0;
即指数型的变幅杆频率方程为k’1 =π。
又因为纵波传播的速度是:
C1= ;
观察可得在变幅杆中声波传播的速度和圆频率有关,且只当<1时才能传播。这就是需要工作频率f>。
结合关系式从而推出半波谐振长度:
L= 。
3.3.2位移节点
由边界条件以及上述公式可以推出质点位移ξ沿轴向的分布:
ξ=ξ1 ;
把x=x0,ξ=0代入,得位移节点x0:X0=。
3.3.3放大系数
根据质点位移分布,当x=l时候,ξ=-ξ1,从而得出放大系数:
M1=.
再将共振条件k’l=π代入,就可以得到最终的放大系数M1:
M1==N。
3.3.4形状因数
从公式中可以看出,pc,即为变幅杆的材料特性力阻抗值越小,要使末端的振动速度或者振幅尽可能大,还应选择形状因数大的材料,所以φ值也是一个重要的参数之一。
应变沿着杆的轴向分布表达式为
;
再由极值条件可以得到应变极大值为
=;
代入ξ值
Φ1=N 。
3.4悬链线形变幅杆
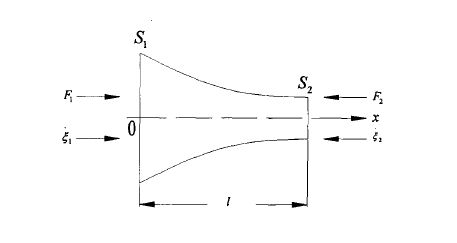
图3.悬链线形变幅杆
如图所示,此为悬链线形,再假定左边一面在坐标原点处,当X=0时面积为S1.直径为D1;另一端处于X=L处,横截面积为S2。直径为D2。
所以可得其中的直径为D=D2;;
根据总振动的波动方程,可以得出其的位移解是
ξ=
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: