矿井围岩的动力响应外文翻译资料
2021-12-11 21:52:01

英语原文共 6 页
矿井围岩的动力响应
摘要
矿场的任何墙控项目都应自然地包括了解坑壁对爆炸荷载的动态响应。如果爆破靠近坑壁底部并且在适当的频率范围内具有足够的能量,则它们可以引起壁的重要部分的动态运动。在这方面,确定坑壁的自然(共振)行为很重要。不幸的是,这种共振行为不能使用全尺寸爆炸来确定,仅仅因为自然响应受到爆炸延迟序列影响的光谱污染。因此,通过模拟为短持续时间宽带位移脉冲的单个爆炸事件来加载(在其基部)感兴趣的坑壁。在本研究中,使用动态有限元法(DFEM)确定对这种载荷的壁响应。二维和三维模型的DFEM结果表明,即使对于弹性情况,也不可能在任何强共振模式下激发壁。这种弱(有损)共振是由于显着的辐射阻尼引起的,其中振动能量分布在周围区域内,并且不会在墙壁区域内进行修复。对于弹性和粘弹性材料的壁,获得了详细的响应,并且具有受损的顶部区域;在所有情况下,最明显的运动总是在墙顶区域发现。然而,由于共振较弱,在任何实际意义上不可能明确地识别墙壁共振行为,这表明与单个(种子)炮眼的现场测量结果一致。根据这些结果,无论多么大规模的爆炸的延迟精度如何, 通过改变爆炸延迟序列来控制壁响应的可能性很小。
关键词: 动态响应;坑壁共振;爆炸加载;数值模型
导言
任何矿场墙体控制程序的一个重要组成部分在爆炸载荷下都需要了解动态响应。如果坑内爆炸在适当的频率范围内具有足够的能量,那么它们可以引起一部分坑壁的动态运动,特别是如果爆炸物靠近墙壁的底部。在这方面,Blair1提出了足够大的爆炸可能引起整个墙壁部分的全身共振的可能性。他还描绘了一个动态扭曲的墙壁轮廓,这个轮廓看起来与特定护堤的脚趾和顶部的测量振动一致。检测任何可能的共振的标准方法是使用传递函数方法,其涉及选择参考测量点(例如底端),具有测量的幅度响应A1(f),作为频率f的函数,和目标测量点(如底端峰)的函数,具有相位幅度响应A2(f)。估计目标点相对于参考点的相对响应的传递函数由谱比A2(f)/ A1(f)给出。基于这种方法,Blair1的结果表明,对于感兴趣的部位,波峰相对于墙基的最大相对响应是2.7并且发生频率在24.9Hz最近,Osterman2还使用传递函数方法来研究坑壁共振。
任何结构(例如隔离球体,地下洞室或露天矿坑)的动态响应不仅取决于材料特性,还取决于结构的尺寸和形状以及施加载荷的位置和源特征 。例如,均匀弹性材料的隔离球将在径向冲击下表现出强烈的共振响应。这是因为冲击能量基本上仍然被困在球体内。实际上,对于完美真空中的完全弹性和非接触球体,经典物理学指示响应将在有限时间内持续存在。如果这样的球体是粘弹性的,那么响应仍将是共振的,但会随着时间而减小。另一方面,均匀且无界的弹性材料中的地下开口将仅对周围材料中的冲击表现出弱的共振响应,并且该响应将随时间减小。在这种情况下,冲击能量不会保留在开口附近并且辐射到周围材料的有限范围内。在结构动力学领域,这种损失机制被分类为辐射阻尼;它的特点是有损谐振响应,即使在完全弹性的材料中也是如此。这些有损模式的一个例子在Blair3的图3中给出,其分析了圆柱形空腔在受入射平面P波影响的均匀弹性材料中的响应。这些模式是可观察到的非常弱的共振,因为传递函数中的小振荡表示圆柱形腔的响应。 Siggins和Stokes4给出了有损模式的另一个例子,他们分析了大弹性地下开口对施加到开口顶部的垂直力的响应。这种载荷是在开口边界上的弹性表面波的有效发生器。 Siggins和Stokes4在其传递函数中表现出适度的振荡,表示地下开口的响应。 3中的弱共振和4中较强的共振是由于开口边界上的循环瑞利波引起的;有损模式的产生是因为这些表面波的振幅随着时间逐渐减小,即使对于完全弹性的材料也是如此。
井壁在底部受到单一爆炸事件的冲击时,也不能有效地捕获输入能量。在这种情况下,产生的振动波与垂直和水平表面相互作用,垂直和水平表面反射入射能量,同时产生表面波;所有这些波随后将离开基坑壁区域。换句话说,壁面反应只持续与爆炸事件类似的时间。因此,在这种情况下,预计基坑壁面将遭受显著的辐射阻尼,因此即使对于弹性材料,也只表现出微弱的共振响应。这一理论基础并不支持Osterman2的观点,他从生产爆破数据的分析中得出结论,高壁表现出强烈而清晰的共振(见图12)。然而,任何生产爆破都只是单个炮眼事件的延迟序列,Osterman2将壁面共振与该延迟序列的影响混为一谈。第8节将更详细地考虑这方面。
与3和4中介绍的案例不同, 与坑壁相关的辐射阻尼没有解析解。因此, 利用数值模型寻求解决这一难题的办法。因此, 本工作的主要目的是利用动态有限元模型 (DFEM) 来研究坑壁 (特别是其顶部区域) 由于墙底部的单一爆炸事件而产生的反应。
坑壁的二维模型
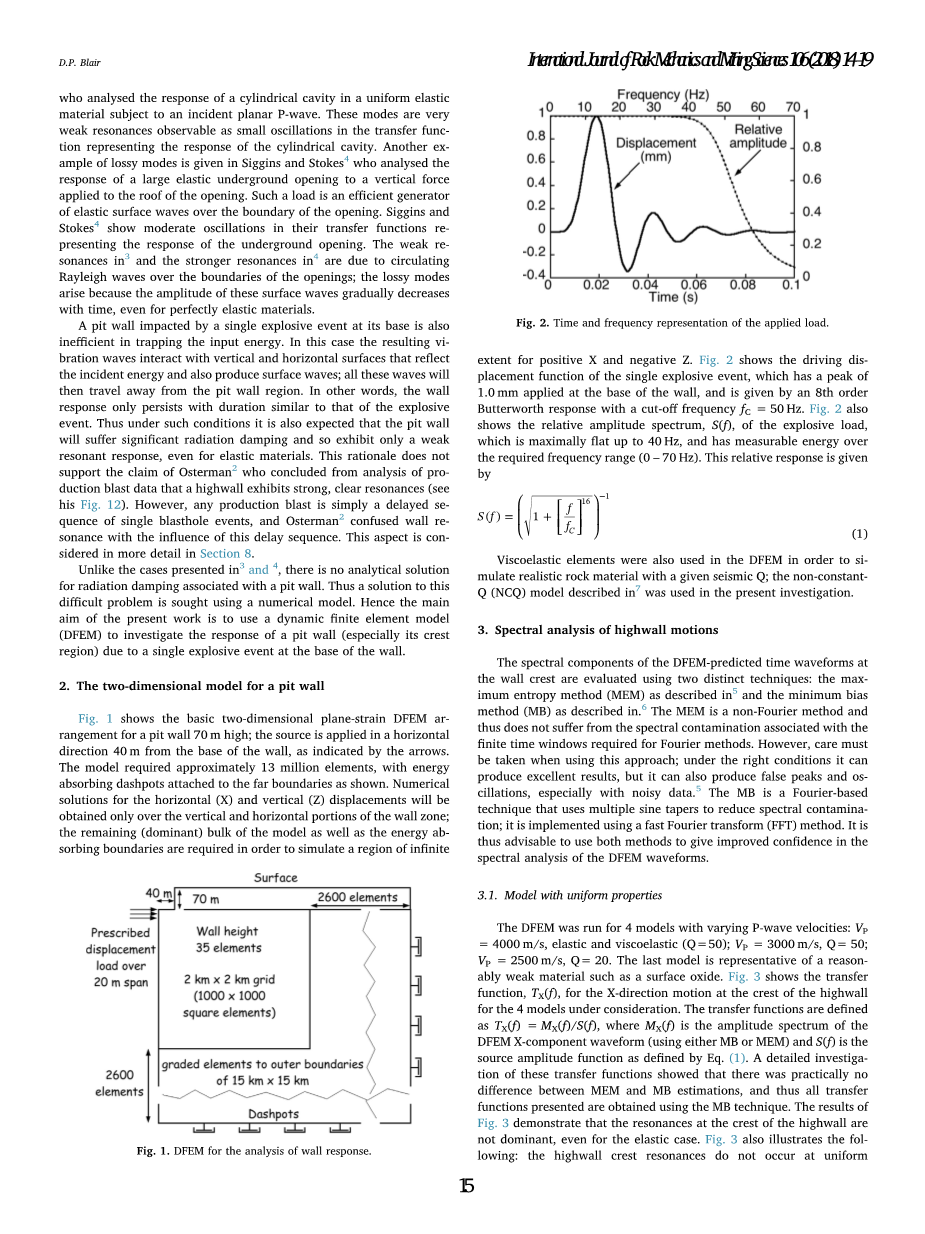
图1示出了用于70m高的坑壁的基本二维平面应变DFEM布置;源于箭头所示的水平方向40m从壁的底部施加。该模型需要大约1300万个元素,如图所示,附着在远边界上的能量吸收缓冲器。水平(x)和垂直(z)位移的数值解将只在墙区的垂直和水平部分获得;模型的剩余的(占主导的)体积和能量吸收边界是为了模拟一个区域中的一个区域。 图2示出了单个爆炸事件的驱动位移函数,其在壁的底部施加1.0mm的峰值,并且由第八阶巴特沃斯响应给出,其具有截止频率fc= 50Hz。图2还示出了爆炸载荷的相对振幅谱S(f),其最大值在40Hz以下,在相应的频率范围(0~70Hz)上具有可测量的能量。这个相对响应是由
图一.用于分析墙体响应的DFEM
图二.时间和频率表示施加的荷载。
在DFEM中也使用了粘弹性元素,以模拟具有给定地震Q的真实岩石材料; 在本研究中使用了7中描述的非constantQ(NCQ)模型。
1高墙运动谱分析
使用两种不同的技术评估墙顶处DFEM预测时间波形的光谱成分:如5所述的最大熵法(MEM)和如6所述的最小偏差法(MB)。MEM是一种非傅立叶方法,因此不会影响与有限时间窗相关的光谱污染。要求傅立叶方法。但是,使用这种方法时必须小心;在正确的条件下,它可以产生良好的结果,但也可以产生假峰值和振荡,尤其是在有噪声的数据中。5 MB是一种基于傅立叶的技术,它使用多个正弦锥度来减少光谱污染;它是使用快速傅立叶变换(FFT)方法实现的。因此,建议使用这两种方法来提高dfem波形光谱分析的可信度。
-
- 具有均匀特性的模型
DFEM运行4个模型,具有不同的P波速度:VP = 4000m / s,弹性和粘弹性(Q = 50); VP = 3000m / s,Q = 50; VP = 2500m / s,Q = 20。最后一个模型代表了一种相当弱的材料,如表面氧化物。图3显示了转换函数TX(f),用于考虑高墙的4个模型顶部的X方向运动。传输函数定义为TX(f)= MX(f)/ S(f),其中MX(f)是DFEM X分量波形(使用MB或MEM)的幅度谱,S(f)是源幅度函数,由下式定义:式。 (1)。对这些传递函数的详细研究表明,MEM和MB估计之间几乎没有差异,因此所有传递函数都是使用MB技术获得的。图3的结果表明,即使对于弹性情况,高墙顶部的共振也不占优势。图3还说明了以下情况:高墙波峰共振不是以均匀的频率间隔发生的;随着频率的增加,粘弹性材料的振幅逐渐减小(VP = 4km / s的结果);随着材料速度的降低,频率降低,降低Q值对降低传递函数有显着影响,而降低材料速度的影响较小。
图三.传递函数波峰运动;只有X-成分
-
- 非均匀性模型
本节考虑的第一个模型是,对于具有三个水平层的高墙,所有具有Q = 50描述的衰减。 上(弱)层(50-70m)的速度VP = 2.4km / s; 中间层(20-50m)的VP = 3.2km / s,下层(0-20m)的VP = 4.0km / s。 图4显示了顶部水平(X)和垂直(Z)运动的传递函数。 在所有频率(45Hz附近的窄带除外)中,对于VP = 4km / s和Q = 50,图4中的X分量传递函数明显大于图3中所示的X分量传递函数。 这与低强度顶层在固定动态位移载荷下表现出相对大的位移的预期一致。
图四.传递函数三层墙模型的峰顶运动。
考虑的下一个模型是针对波峰损坏的情况。 在该模型中,由峰值限定的尺寸为10mtimes;10m的区域被假定为由VP = 2.4km / s描述的弱(损坏)材料,其中地震衰减由Q = 20给出。 剩余的材料具有VP = 4km / s和Q = 50的特性。 图5显示了该波峰损伤模型中波峰处水平和垂直运动的传递函数。
图五.传递函数拱顶损伤模型的峰值运动。
图3,4和5展示了爆炸事件下高墙顶部区域运动的三个非常重要的特征。首先,该运动仅表现出宽的光谱特征。 换句话说,波峰没有任何强烈或良好定义的共振行为。 其次,光谱峰之间通常没有均匀的间隔。 第三,这些光谱特征的确切性质取决于物质性质和它们的分布。这三个特征意味着很难(如果不是不可能的话)使用任何测量的光谱响应来推断特定的高墙的共振行为。
2高墙的颗粒运动
高墙的基部,墙壁和表面上的粒子运动可以在每个感兴趣的测量点处以声像图(X-位移与Z-位移的图)的形式表示。因此,声像图显示了墙壁粒子运动的轨迹。然而,粒子运动(通常为毫米)比测量站的坐标值(通常为毫米)小几个数量级,因此出于显示目的,必须放大粒子运动。图6显示了沿着高墙基部,墙壁和表面的选定点的这些声像图;所有粒子运动都被放大了20,000倍。因此,在图6的刻度上的20m的位移表示1mm的实际壁位移。结果以三种模型的设定图给出:均匀的弹性材料,VP = 4000m / s;三层模型;和如前所述的波峰损坏模型。均匀和3层模型的基础声像图存在轻微差异,原因很简单,因为前者是在一个弹性材料中,其中是弹性材料(Q = 50)。损伤模型的基础声像图实际上与3层模型的基础声像图相同(因此未示出),基区在两种情况下都是相同的。图6显示了所有型号的墙顶处的大位移。每个声像图(零X和Z动态位移)的起源被视为每个墙站的小点状暗区。因此,关于波峰点,可以看出大波峰运动是向外或向下或向后和向上。为了进一步了解墙体运动,图7显示了墙体形状随时间变化的变化;在这个例子中,粒子运动已经放大了12,000倍。两个单独的模型以o ff设置形式显示;统一的弹性模型和3层模型,以及这些模型,在三个指定的时间表示墙壁的形状。例如,在0.059s的时间,均匀模型显示从墙壁向下和向外的最大第一运动,之后,在0.072s处,显示在相反方向上的最大运动。隔离墙没有其他主要的位移;换句话说,墙壁运动受到严重阻尼。 3层模型显示类似的特征分别在0.067s和0.083s的较长时间发生。这些较长的时间是由于3层模型的上层中较低的波速。图7的粗线之间的浅灰色阴影在所考虑的时间间隔内仅是所有壁形状的高密度。同样明显的是,3层模型中的失真比均匀弹性模型中的失真更多,特别是在后期,这很可能是由于分层模型中的混响。
图六。三种模型的DFEM热图,均显示出较大的峰值移位。
图七。在特定的时间内形成顶点;第一次大的运动是向外和向下的。
图8显示了3层模型的整个感兴趣的壁区域中的矢量峰值粒子位移(VPPD)。 该图突出了高墙位移的复杂性质,其中顶部运动占主导地位,并且发现3层模型的表面运动大于均匀模型的表面运动(结果未显示)。 如前面关于图4的传递函数结果所述,这与期望低强度顶层在固定动态位移载荷下表现出相对大的位移是一致的。 在图8中也可清楚地看到该层受Z = 50m和表面限制的影响,并导致在图7中所示的0.067s时的大的“向外和向下弯曲”。
图八。VPPD贯穿整个壁区;3层模型。
- 多台阶坑的二维模型
到目前为止,只考虑了一个高墙,并且发现在动态载荷下在顶部有最大振动。现在值得研究一个露天矿中许多山峰和护堤的墙壁的运动。这里考虑的特定模型与图1所示的模型相同,只是70米的垂直墙被7个小的垂直墙所取代,每个墙高10米,每个护堤宽度都有8米。为了同时显示几何和某些DFEM结果,在一幅图中,图9显示了坑壁表面上的矢量峰值粒子位移(VPPD); 这是(X,Z,VPPD)的三维轮廓。 在大多数工作台上,顶部有动态运动的放大,这也与之前单个高墙的结果一致。 然而,有一些波峰的放大是小的,这是由于复杂性质的波在多个台阶上传输。
图九.峰值位移,7级壁面-显示峰值放大。
图10显示了墙壁形状随时间的变化;在这个例子中,粒子运动已经被8000的因子所限制。较低的一组壁形状对应于0.025-0.050s的时间范围,而较高的一组对应于0.065-0.09s的时间范围。因此,对于lt;0.05s的时间,主振动没有达到上护堤,其仍保持相对不受干扰; 对于gt; 0.065s的时间,主要振动已经到达上台阶,下台阶的振动减弱了。很多年前,布莱尔推测,在任何特定的时间,整个板凳都会呈现出独特的“共振”形状(见图11)。目前的分析表明,这种推测是错误的,原因有两个。首先,它假设壁运动是持久的(即共振),其次,它忽略了振动的有限传播时间。然而,实际上,图10显示,在任何时候,只有部分工作台在动态负载下会表现出显着(但非持久性)的变形。图11显示了顶点和脚趾点以及X和Z运动方向的传递函数; 这些图中的每一个都是7点的响应平均值。 结果表明,在足够低的频率下,X分量占主导地位,并且对于足够高的频率,最大运动大于脚趾运动。此外,对于频率范围的重要部分,波峰运动支配这些传递函数; 这与图9中所示的VPPD值一致。
图十。两种特定时间范围内的板壁形状。
图11.平均传递函数7台模型。
-
<li
资料编号:[5759]
</li




