采用严格的极限平衡法对三维斜坡进行稳定性分析外文翻译资料
2022-09-06 11:42:58

英语原文共 13 页,剩余内容已隐藏,支付完成后下载完整资料
采用严格的极限平衡法对三维斜坡进行稳定性分析
X.P. Zhou, H. Cheng
a土木工程学院,重庆大学,重庆400045中国
b山区城市建设国家新技术重点实验室,重庆大学,教育部,重庆400045中国
C煤矿灾害动力学及控制国家重点实验室,重庆大学,重庆400045中国,
关键词:三维坡 稳定性 极限平衡法 安全系数 最小二乘拟合
摘要:
以前只有满足三个方向的力的平衡,和一个或两个方向力矩平衡的三维斜坡或者滑坡的稳定性可以用准严格限制平衡的方法来分析。在本文,严格极限平衡柱法,其中柱间力的考虑,是基于六个平衡条件,其中包括围绕三维坐标轴建立的在三向力平衡条件下沿坐标轴和三个方向的力矩平衡条件。使用信任域反射迭代算法来确定滑动体和安全系数的宽度之间的关系。安全系数的值是使用非线性最小二乘法得到的。此外,此方法还可以应用于自动搜索三维滑坡滑动面和确定三维滑坡与已知任意滑动面安全系数。对三个实例进行了讨论,详细地说明和验证本方法的可行性和精度。与准严格极限平衡方法只考虑四个或五个平衡条件相比,本方法更为准确和严谨。
- 简介
山体滑坡被定义为岩体,岩屑或泥土沿斜坡向下的运动(克鲁登,1991)。它们可以通过各种外部刺激来触发,如地震,强降雨,
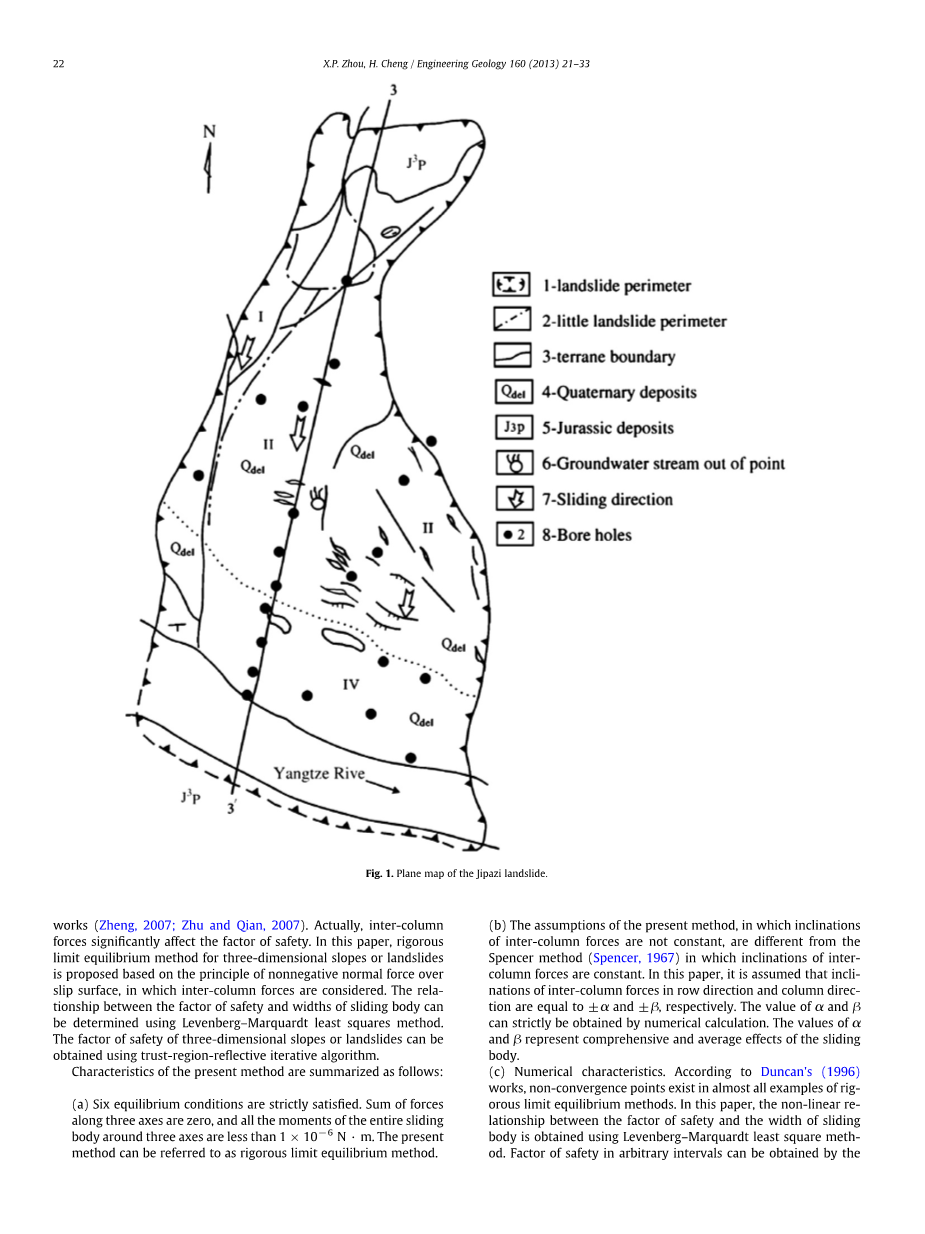
水位变化,人为干扰或急流侵蚀等等。滑坡是一种主要的自然灾害。如图1所示,鸡扒子滑坡的主要原因是激烈的降雨发生在七月的四川省的1982。鸡扒子滑坡的体积约为1500万立方米,约有1700栋房屋被摧毁。鸡扒子滑坡造成了巨大直接和间接两方面的损失。
图1 鸡扒子滑坡的平面图
目前,常规的极限平衡方法在实际的斜坡或滑坡工程仍然发挥了重要作用。特别是,极限平衡方法被广泛和成熟应用于分析二维斜坡和山体滑坡的稳定性。对于二维边坡或滑坡,使用满足所有平衡条件的极限平衡方得到的安全系数是足够精确的(邓肯,1996)。然而,对于实际的边坡或滑坡工程,斜坡或滑坡是三维问题,不适合被简化为二维的。以前,应用极限平衡法对三维边坡或滑坡稳定性进行了研究,仅对部分平衡条件进行了满足,而不是在严格极限平衡法的框架下进行的。例如,只有三种平衡条件都满足,这仅适用于对称斜坡和滑坡(Hungr,1987;Zhang,1988;Hungr等人,1989;Lam和Fredlund,1993),只有四五个平衡条件得到满足(Chenetal,2001a,2001b;Huangetal,2002;Zhangetal,2005)。此外,从准严格限制平衡法获得的安全系数,是不能完全满足工程要求的(Baligh和Azzouz,1975,Hovland,1979; Hungr,1987;zhang,1988; Hungr等人,1989; Lam和Fredlund,1993; Feng等,1999; Huang 和Tsai,2000;cheng等人,2001a,2001b。 Cheng等人,2002; Huang等人,2002)。
当用严格极限平衡法分析三维斜坡和山体滑坡的稳定性,六个平衡条件都应该得到满足,即三维数轴上三个方向的力平衡条件和力矩平衡条件都满足。到现在为止,满足所有的六个平衡条件的丰硕的成果却很少。例如,基于非柱法研究三维边坡或滑坡的极限平衡法。(郑2007)。三维斜坡或滑坡的严格与准严格极限平衡稳定性分析的区别在于使用方法,其中在滑动面正应力由五个参数的函数修正。(Zhu 和 Qian, 2007)。然而,在他们的工程中没有考虑到柱间的作用(Zheng, 2007; Zhu 和 Qian, 2007)。实际上,柱间的作用明显影响着安全系数。本文基于非负法向力原理,提出了三维边坡或滑坡的严格极限平衡法,并在此基础上考虑了桩间的相互作用。滑动体的安全系数与宽度的关系采用最小二乘法确定,滑坡三维边坡安全系数也可以使用信任域反射迭代算法得到。本方法的特点总结如下:
(a)六平衡条件均严格满足。沿三个轴的力的总和为零,且对整个滑动体的周围的三个轴的总是小于1times;N·m的。本方法可以称为严格极限平衡法。
(b)本方法的假设,在基于柱间作用力倾向不是恒定的,不同于斯宾塞方法(Spencer,1967),柱间力量的倾向是不变的。在本文中,假定柱间力行方向和列方向的倾角分别等于plusmn;alpha;和plusmn;beta;。通过数值的计算,可以得到很严格的alpha;和beta;的数值。alpha;和beta;的值代表的是滑动体的综合性和平均效应。
(c)数值特征。根据Duncan的的工程,在几乎所有的例子中存在着非收敛点的严格极限平衡法。在本文中,安全系数和滑动体的宽度之间的非线性关系是采用Levenberg Marquardt最小二乘法得到的。通过拟合曲线得到任意区间的安全系数。即使在一些很短的时间间隔中,数值结果也不收敛,安全系数可以由拟合方程准确地确定。因此,在本方法中,存在着良好的数值特征。
(d)在本方法中,任意滑动面都可以被考虑不仅限于椭圆滑动。
- 严格极限平衡法原理
2.1作用于柱上的力
滑动体被划分为若干与接口垂直的列,如图2所示。每一列都是以字母为标记的,这代表了行和列的数目。有在x方向和y方向上分别有n列和m列。所有的力作用于柱的示意图如图3所示。柱的权重被表示为。作用在滑动表面上的法向力和剪切力分别表示为和。孔隙水压力作用在光滑表面上表示为。柱(i,j)和柱(i,j-1)之间的柱间力被表示为,柱(i,j)和柱(i-1,j)的柱间力的被表示为。
2.2基本假设
柱的方法是不确定的,其中的未知数的数目远远大于公式数目。因此,有必要作出关于柱间力的各种假设,使问题确定。
(a)假设柱的底部是平面,并且法向力,剪切力和孔隙水压力作用在平面的中心的点(I)。另外,重力作用在柱的质心(H),是指向(Ⅰ),如图3所示。
(b)假设各柱力和分别平行于yz平面和XZ平面,根据滑面的几何特征,柱间力的倾角是plusmn;alpha;,如图3所示(的倾角为alpha;时,和z轴方向之间的角度大于90°; 的倾角为-alpha;时,和z轴方向之间的角度小于90°)。同样,柱间力的倾角是plusmn;beta;,如图3所示(的倾角为beta;时,和z轴方向之间的角度大于90°; 的倾角是-beta;时,和z轴方向之间的角度小于90°)。
(c)假设滑动体运动方向或可能变化的方向与X轴方向相反。
(d)假定在三维边坡中没有支撑结构,如挡土墙。
(e)假设土壤的抗拉强度是零。
2.3几何模型
如图2所示,坐标系O-XYZ成立,其中,x轴是滑动体的运动的反方向,y轴是平行于滑动体宽度的方向和z轴的方向是平行于滑动体的高度的方向。整个滑动体被放置到第一象限。地面和滑动体表面分别由方程=g(x,y)和 = f(x,y)描述。法向力在滑动面的余弦方向表示为(,,),剪切力在滑动面的余弦方向表示为(,,)。由于正常的力与轴之间的夹角小于90°,所以的值必须为正。因此,在余弦方向超过滑动面正常的力被描述为
(,,)=(,,) (1)
其中△=, (2)
由于X轴平行于该滑体运动的方向,可以得到
(,,)=(1,,) (3)
其中△=。 (4)
柱的权重为=gamma;[g(x,y)- f(x,y)] (5)
其中,gamma;表示滑动体的平均单位重量,表示柱的横截面面积。
图2 三维滑动面示意图
- 限制平衡方程
3.1柱的力平衡方程
平衡力沿x轴的方程
( ) cosbeta;- cosbeta;=0。 (6)
平衡力沿y轴的方程
( ) cosalpha;- cosalpha;=0。 (7)
平衡力沿z轴的方程
( ) sinbeta;-sinbeta; sinalpha; sinalpha;-=0。 (8)
3.2整个滑动体的力矩平衡方程
根据假设(d)中,有滑动体没有支撑结构。因此,柱间的边界条件
可以被描述为=0,=0,=0,和=0。
因为其他柱之间力的作用力与反作用力的关系,柱间的力的轴线周围的力矩等于0,力矩平衡等式可以如下表示。
绕X轴的力矩
{-[( ) ] [( ) ]-}=0 (9)
绕Y轴的力矩
{[( ) ]-[( ) ] }=0 (10)
绕Z轴的力矩
{-[( ) ] [( ) ]}=0 (11)
其中
是力点或的X轴上的坐标(的柱间力在图3中平面ABBA与平面CDDC的不同的值。是在图3在平面BCCB与平面ADDA中不同的柱间力的值),这等于在H点的X轴坐标。
图3 柱上的力示意图
是力作用点或的Y坐标,这等于H点的Y轴坐标。
是力作用点或的Z坐标,这等于H点的Z轴坐标。
等于H点的X轴坐标。
等于H点的Y轴坐标。
安全系数被定义为因子通过该剪切强度部件必须降低以使土体成沿一选定的滑动面限制平衡状态。另外,假设的剪切强度和剪切强度的摩擦部件的粘合成分的安全系数是相等的,和在滑动面的剪切力由莫尔 - 库仑准则来确定。可以得到
= (12)
其中表示的是有效的内摩擦角和土壤的凝聚力,安全系数被表示为Fs。
在图3中平面ABB′A和CDD′C′的柱间力的不同的值表示为,那么可以写成下面的表达式
=-。 (13)
同样,在图3中柱间力在平面BCCB与平面ADDA上△表示不同的值,那么,可以写成如下表达式
=-。 (14)
把方程(13)和(14)代到方程(6),(7)和(8)中。
( ) cosbeta;=0
( ) cosalpha;=0
( ) sinbeta; sinalpha;-=0
把方程(12)代入方程(15),(16)和(17)中,消除数和,可以作为得到以下表达式
方程(18)和(19)可以被改写为
(20)
(21)
其中
=cosalpha;sinbeta;(Fs tan) (22)
=cosbeta;sinalpha;(Fs tan) (23)
=cosalpha;cosbeta;(Fs tan) (24)
=cosalpha;sinbeta;(c Fs-tan) (25)
=cosbeta;sinalpha;(c Fs-tan) (26)
=cosalpha;cosbeta;(-c-Fs tan) (27)
= cosalpha;sinbeta;(c-2tan) (28)
= sinalpha;cosbeta;(c-2tan) (29)
=- cosalpha;cosbeta;(c-2tan) (30)
= cosalpha;cosbeta;Fs (31)
= -cosalpha;cosbeta; tan (32)
方程(22) - (32)的物理意义如下
(a),和分别是柱间力在x,y和z方向的方向和滑动面的正常力量的几何特征和剪切力的影响参数。
(b),和分别是剪切力的方向的影响参数和孔上在x,y和z方向上的法向力的水压。
(c),和分别是在x,y和z方向上影响参数和孔上的剪切力的水压。
(d)和分别为柱对正常力和剪切力的权重影响力的参数。
在滑动体的边界上,有可能存在负的法向力。因此,负的法向力应修改以满足假设(e)所示。它是从研究例示出其上的法向力是负的列数少。数值结果,如果这些列被忽略(yang 和Chen,2002),在实际的公差范围内只受到轻微的影响。
把方程(20)和(21)代到方程(9),(10)和(11)中
(33)
(34)
(35)
有三个未知参数alpha;,beta;和Fs的上述三个方程。因此,方程(33),(34)和(35)可以改写为一组非线性方程组:
)=0
)=0
)=0
其中
)=
)=
)=
该组非线性方程(36)可以用信赖域反射迭代算法来解决。初始值被设定为alpha;= 0,beta;= 0,和FS =1。然后局部最优解,可以通过迭代约10-20次获得。该解决方案可以使组非线性方程(36)满足
)le;N·m
)le;N·m
)le;N·m
因此,该解决方案可以视为满足围绕三个坐标轴的整体力矩平衡条件。这个三维斜坡安全的因素是Fs的值。
-
计算已知椭球滑面三维边坡或滑坡的安全因素 剩余内容已隐藏,支付完成后下载完整资料
资料编号:[146866],资料为PDF文档或Word文档,PDF文档可免费转换为Word




