论文总字数：22936字

摘 要

无轴承异步电机是一种结合了磁轴承长处和传统异步电机优良性能的电机。和其余电机相比较，其具备构造简单、转矩脉动小、可靠性高等诸多长处，在控制领域具有较高的运用价值。为了更加快速、可靠地对无轴承异步电机的多变量相互耦合的转子悬浮控制系统进行控制，需要研究多种无轴承异步电机悬浮系统控制策略，优化基于传统PID控制的无轴承异步电机运行性能。

近年来，分数阶微积分理论在控制领域尤其是电机控制领域有了越来越多的应用。本文设计出适用于无轴承异步电机悬浮控制系统的分数阶PID控制器，以抑制无轴承异步电机运行过程中转子质心偏离既定位置，达到较好的电机转子悬浮控制效果。

本文首先推导出无轴承异步电机悬浮控制系统的数学模型，并针对悬浮控制系统中两个方向上的运动控制设计出对应的分数阶PID控制器，以提高对因转子质量不平衡等因素引起的振动的高效快速抑制，达到提高无轴承异步电机悬浮控制系统性能的目的。本文还进一步研究了分别使用整数阶PID控制器和分数阶PID控制器时系统的鲁棒性。

关键词：无轴承异步电机；分数阶PID控制器；悬浮控制系统；鲁棒性;Simulink仿真

Abstract

A bearingless asynchronous motor is a kind of motor that combines the advantages of magnetic bearings with the excellent performance of conventional asynchronous motors. By comparing with the remaining motors, bearingless asynchronous motor has a lot of good qualities and high application value in control field. In order to improve the rotor suspension accuracy of bearing-less asynchronous motors, it is necessary to study various control strategies of bearing-less asynchronous motor suspension system to optimize the performance of bearing-less asynchronous motor operation based on traditional PID control.

In recent years, fractional order calculus theory has been developing rapidly in the field of control, and more and more scholars have started to apply fractional order calculus theory to motor control systems. In this thesis, a Fractional Order PID controller is designed, which is suitable for the suspension control system of bearingless induction motor, in order to restrain the rotor's center of mass from the fixed position during the operation of bearingless induction motor, and achieve a better suspension control effect.

In this thesis, a mathematical model of the suspension control system for bearing-less asynchronous motors is firstly derived, and an analogous fractional order PID controller is designed for the control in both two directions of the suspension control system to improve the efficient and rapid suppression of vibration caused by rotor mass imbalance and other factors, in order to improve the performance of the suspension control system for bearing-less asynchronous motors. In addition, the robustness of the system with integer order PID controller and Fractional Order PID controller is studied.

Key Words：bearingless induction motors；fractional order PID controller；suspension control system；robust；simulink

目 录

第1章 绪论 1

1.1 无轴承异步电机 1

1.1.1 研究现状 1

1.1.2 发展方向 2

1.1.3 应用领域 3

1.2 分数阶控制 3

1.3 研究意义和内容 4

1.3.1 内容 4

1.3.2 意义 4

第2章 无轴承异步电机模型 6

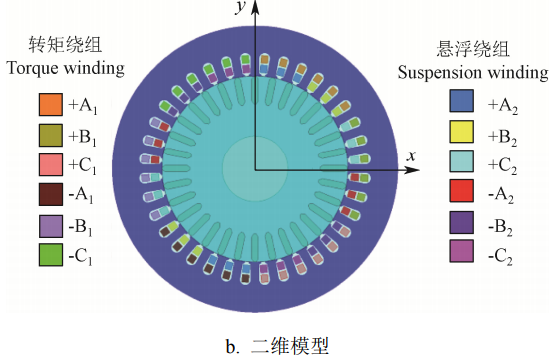
2.1 基本结构 6

2.2 运行机理 6

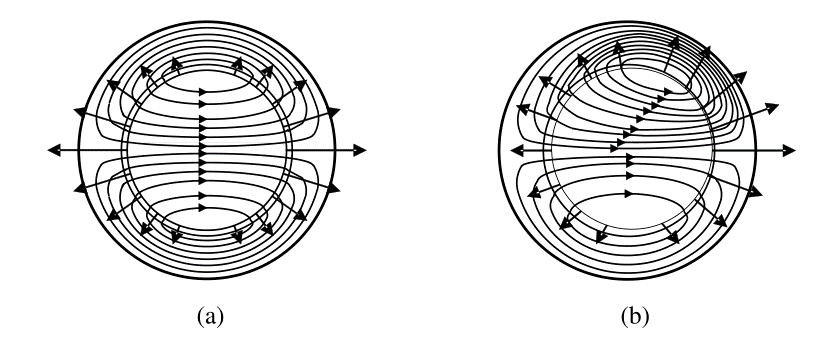
2.2.1 洛伦兹力 8

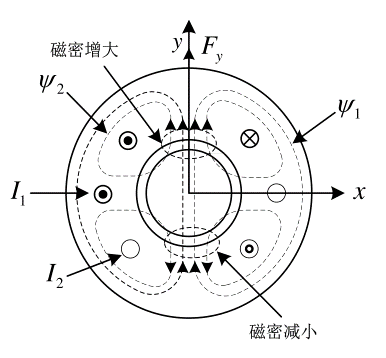
2.2.2 麦克斯韦力 8

2.3 数学模型 11

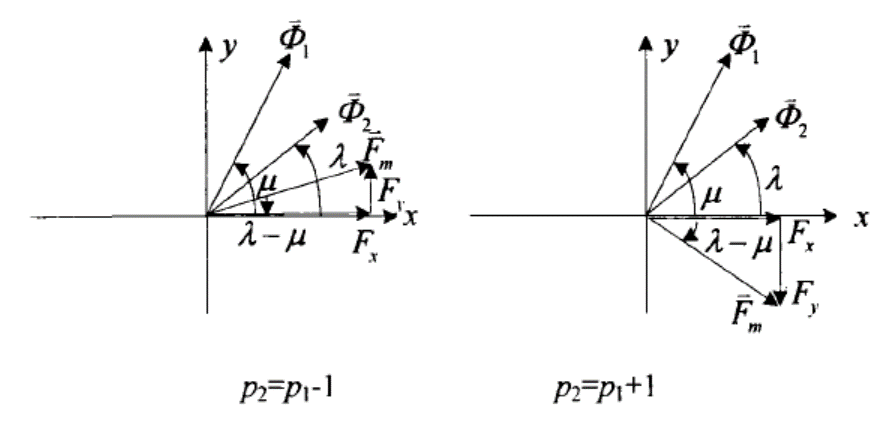
2.3.1 径向悬浮力 11

2.3.2 旋转部分 12

2.3.3 悬浮系统转子运动方程 12

2.4 磁场定向控制 13

2.4.1 气隙磁场定向控制 13

2.4.2 转子磁场定向控制 15

2.4.3 技术比较 16

2.5 基于气隙磁场定向的悬浮控制系统 16

2.6 本章小结 17

第3章 分数阶PID控制 18

3.1 分数阶微积分理论 18

3.2 分数阶控制系统 18

3.3 分数阶PID控制器 19

3.3.1 数学模型 19

3.3.2 稳定性分析 20

3.3.3 实现方法 21

3.4 本章小结 22

第4章 悬浮系统分数阶PID控制器仿真 23

4.1仿真模型 23

4.1.1 转矩绕组控制器 24

4.1.2 悬浮绕组电流计算模块 25

4.1.3 悬浮力计算模块 26

4.1.4 悬浮系统运动模型 26

4.2 仿真实验 27

4.2.1 旋转部分仿真结果 27

4.2.2 悬浮控制系统仿真结果 30

4.3 控制效果对比 31

4.3.1启动过程 31

4.3.2 更改给定值 33

4.3.3 鲁棒性 35

4.4 结果分析 36

4.5 本章小结 36

第5章 总结与展望 37

参考文献 38

致谢 40

第1章 绪论

1.1 无轴承异步电机

无轴承异步电机（Bearingless Induction Motor, 简称BIM）具备构造简单、性能稳定和转速较高等优势，在各个工业领域都有着广阔的运用情景。近些年来，无轴承异步电机成为一个较为受关注的电机种类。然而，在无轴承异步电机的使用过程中，如何高效可靠地对电机的悬浮系统进行控制一直是制约无轴承异步电机性能的主要问题。因此，研究无轴承异步电机尤其是其悬浮控制系统具有重要意义。

1.1.1 研究现状

为了获得无轴承异步电动机的良好运行性能，近年来针对无轴承异步电动机的控制方法进行了大量的分析和讨论，无轴承异步电机的控制主要有3类方法。

（一）磁场定向控制

通过对电机的磁链矢量进行人为干预，磁场定向控制技术将电机定子电流进行分解。磁场定向控制技术最常用的方法是气隙磁场定向控制^[1]。

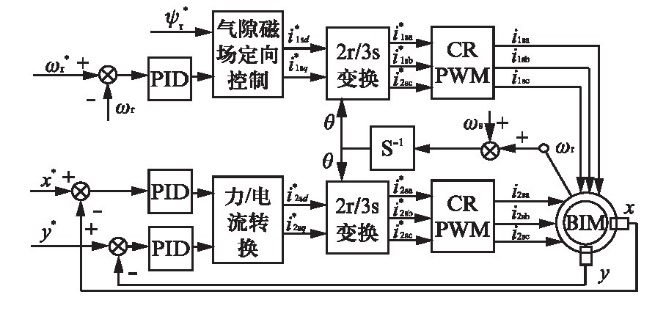
图1.1 一种基于气隙磁场定向的BIM控制框图^[1]

（二）直接转矩控制

直接转矩控制技术能够根据电机电流直接对电机转矩进行控制^[2]。在无轴承异步电机控制领域，将直接转矩控制和电压矢量调制等技术相结合，可以获得较好的运行性能,但是容易产生速度超调及转矩和磁链波动^[3][4]。

（三）非线性解耦控制

文献[5]建立了如1.2图所示的控制系统，实现了转子磁链、转速，以及x方向和y方向上位移之间的非线性动态解耦。

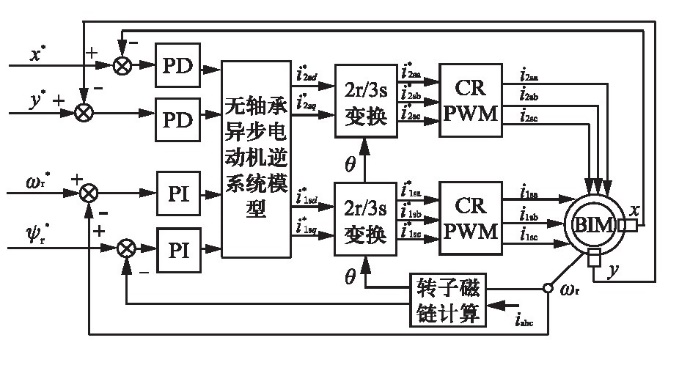
图1.2 非线性动态解耦的BIM控制框图^[5]

除了上述的三种主要控制技术，为保证无轴承异步电动机稳定运行，驱动系统需具有快速响应和抗扰动能力。无轴承异步电机中转子位置控制通常采用传统整数阶PID控制理论。传统整数阶PID控制器难以快速、准确地对外部条件变化做出反应，使得无轴承异步电机在高速运行过程中,容易出现过高超调、振荡以及鲁棒性较差等状况。因此，对无轴承异步电机悬浮控制系统中转子位置控制进行优化设计具有重要意义。

为解决传统PID控制器难以得到最佳调节参数的情况，近年来已提出诸多自适应控制器，如平滑模型控制、模型参考自适应等，但都依赖于系统精确模型。近年来，一些结合人工智能的综合控制策略逐渐增多：为了有效地抑制无轴承异步电动机速度检测对系统稳定性和精度的影响，文献[6]提出了一种使用人工神经网络逆方法的速度观测方案；为了解决无轴承异步电动机在各种干扰和不确定性下的速度响应和系统抖振问题；为了解决无轴承异步电动机在参数变化、外部干扰和负载突变情况下控制性能不理想的问题，文献[7]设计了自适应指数型滑模控制器和扩展型滑模干扰观测器；文献[8]提出了一种使用反向传播神经网络的PID控制策略；文献[9]提出一种新型串联卡尔曼滤波器，能够有效减小电机参数变化和外部环境干扰对系统控制效果的影响。

1.1.2 发展方向

(一)更加准确的数学模型

建立无轴承异步电机的数学模型是开展其他研究的基石。由于无轴承异步电机的旋转部分和普通异步电机具有相似性，因此可以借用异步电动机的数学模型来进行旋转部分的建模。但是由于无轴承异步电机的高度非线性特征，有必要建立能够更加准确反映无轴承异步电机内部物理过程的数学模型，为后续研究提供更为准确的基础^[10]。

(二)悬浮转子质心偏移补偿控制

由于生产制造工艺的不稳定误差，无轴承异步电动机的转子极易出现质量空间分布不均匀的状况，和理想电机模型存在一定误差，进而导致转子受力与理想状况不一致^[11]。无轴承异步电动机的励磁力在启动阶段迅速上升，当达到一定的转速时，系统的稳定性可能会受到破坏^[12]。

1.1.3 应用领域

由于无轴承异步电机具有转速较高且稳定、寿命长等诸多长处，在越来越多的生活场景中得到运用。图1.3为电机在几个领域的典型应用^[13]。

请支付后下载全文，论文总字数：22936字

相关图片展示：