英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

---

调制-滞环电流控制的DC-DC升压转换器的分岔点的估算：稳定性分析和实验验证

摘要：电子电子电路比如DC-DC变换器在非线性现象下的应用很普遍。经常需要判断系统什么时候会不稳定。本文研究了一个时间连续的调制-滞环电流控制器的普遍模型。此模型用于工作在连续导通模式的升压变换器，从而可以估算出分歧点并研究控制系统的稳定性。此控制器确保了固定开关频率，无静差以及高抗干扰能力等系统参数变化。仿真和实验结果验证了该方法的可行性。

1 引言

典型的静止变流器设计用于稳定的一周期操作。电力电子工程师解决了各种电力电子电路中的许多复杂性能。分歧以及混沌现象在世界范围内许多研究中都有所研究。电力电子器件的非线性现象最新研究参考文献[1-7]。

验证非线性系统的动态性能最常用的工具是分岔图。如果允许参数变化，系统也许会放弃均衡解转而寻求其他平衡解。分岔图代表了一个量的采样值，该值作为一个及一个以上分岔参数。在静止变流器中研究的分岔参数有很多其中包括：输入电压，负载电阻，基准电流源电容，开关频率，电感，电感的寄生电阻，电容的串联电阻，反馈增益，斜坡补偿以及功率。

非线性系统的稳定性分析可通过研究基本类型DC-DC变换器来进行，比如buck变换器，boost变换器中的连续与不连续导通模式，buck-boost变换器，可逆boost变化器，单相H-桥逆变器，Cuk变换器以及Luo变换器。

当由于非线性特性而导致分岔参数变化时，可能会出现不同类型的不稳定情况。分岔的类型在文献[1,8,11]中有所讨论。一般情况下，在电力电子系统中常见的两类分岔类型为慢速失稳与快速失稳。假设周期1的稳定轨道存在的话，这两种分岔类型将会导致其丢失。通常在电力电子系统中发现的分岔的类型是Hopf或Neimark-Sacker，鞍节点和周期性倍增或翻转。翻转分岔或周期倍增分岔是失稳快速的分岔的特征，其中周期-1动态被周期2的解所取代。Neimark–Sacker or Hopf分岔是一类慢速分岔，引入了一个周期性极限周期或拟周期解。这些被称作平滑分岔的分岔类型与系统结构性改变无关。但其他被称作边界碰撞分岔或非光滑分岔的失稳情况会随着结构性改变而出现。

许多向逆变器提供控制电流或电压控制器类型已经在文献[27-30]中提出。在[27]中研究了一个具有纹波常数的准时控制buck变换器。在[5]中，离散图被应用于一个在峰值电流模式控制下带有交-直电容整流器的降压-升压变换器，来显示快速失稳性以及使用基于特征值的标准的雅可比矩阵的间歇分岔。使用在峰值电流和滞环电流控制的连续导通模式（CCM）下运行的单端初级电感逆变器（SEPIC）进行分岔分析[8]。二次降压变换器的比例-积分（PI）控制器设计标准在[28]中给出，此标准能在不同的运行点下提供稳定性与鲁棒性。[29]研究了一类压控串级升压变化器的稳定性。三相Vienna整流器中直流环节的理想双层滑移稳定性分析于文献[30]中提出。[31]研究的系统是非线性负载控制下的Cuk变换器功率因数校正，该作者表明此系统会当负载改变时，使用离散时间映射时会出现周期倍增分岔。此外，电脑仿真显示慢速稳定性在系统中有间歇性特性。在峰值电流模式控制下的变换器在[32]中通过计算机仿真进行研究。快速失稳发生于新电感，参考电压，负载电阻以及电容改变时。PI控制器增益与负载转矩变化对包含一个不控二极管整流器、直流环节以及脉冲宽度调制电压源逆变器的工业传动稳定性的影响在[33]中得到研究。[34]研究了一个在自由振荡电流模式控制下的二级级联逆变器。几个电流控制器的对比研究在[35-38]得到体现。

滞环控制器用于产生开关变化器要求的转换信号。他的原理基于自激振荡。这种控制器的优点有高交换带宽、稳定性好且独立于系统参数。

除了高带宽，有趣的是在三相系统中对称倍增视在周波频率脉动的能力。然而，电流控制器的开关频率不是常数，因此很难确定滞环带宽。这种控制器在开关频率附近产生大的边带谐波。这会导致在滤波器中很难去确定像电感电抗无功元件的参数。为了解决这些问题，提出了恒频置换调制。在[24]中，Huerta等人提出数字跟踪开关频率参数改变滞环带宽并将最大波动范围设置为plusmn;0.5%以内。在[44]中，Nejad等人提出了用滑动面调制三角波，包括一个维持恒开关频率并减少稳态静差d积分环节。本文也使用了这种混合电流控制器。对于给定开关频率，滞环调制电流控制器的参数是三角波信号幅值以及滞环带宽。本文将三角波信号幅值看做分岔参数。

现已知使用这些控制器，会出现分岔现象而导致混沌现象。了解分岔什么时候以及怎么产生很重要。这需要合适的建模[1]。在不同的DC-DC变换器建模方法中，在文献中有两种常用的模型：平均模型，时间离散模型[1,46-50]。使用者两种模型，通过估计系统在均衡点雅可比矩阵的特征值能研究稳定性以及鲁棒性。

本文提出了一个平均的方法来模拟一个电流控制器下的CCM升压变换器。慢速分岔可以通过标准平均模型预测。在改进的峰值电流模式控制下[6]，此模型可以用来估算翻转分岔的第一个分岔点。在该模型中会失去渐近稳定性产生了相当于两个周期的周期循环。

此论文的贡献在于相比于文献[6]调整了其他电流控制器模型。该控制器基于调制的滞环[44]。由于控制器要求完全与[6]中的不同，调整模型很重要。在[44]中，Nejad等人用平均模型研究了滞环调制电流控制器平均动态性能。本文相比[44]改进了模型从而能估计平均模型的有效限，通过对比平均模型与开关模型的稳定性丢失可显著发现这一特点。这是个加强版的模型，相比开关模型有很好的近似稳定临界点。

本文提出的模型将被用于其他基于滞环调制控制的非线性电流控制器。我们的的目标是通过估计特征值来研究系统的稳定性。

本文包含5个部分。第二部分中，描述了正在研究中的系统。使用分岔图研究了全局性能，并用几个实例说明。提出的平均模型可用于估计分岔点并验证系统的稳定性。理论结果的综述在第三部分展现。该方法的验证在第四部分以实验结果进行。结论见第五部分。

2 系统说明

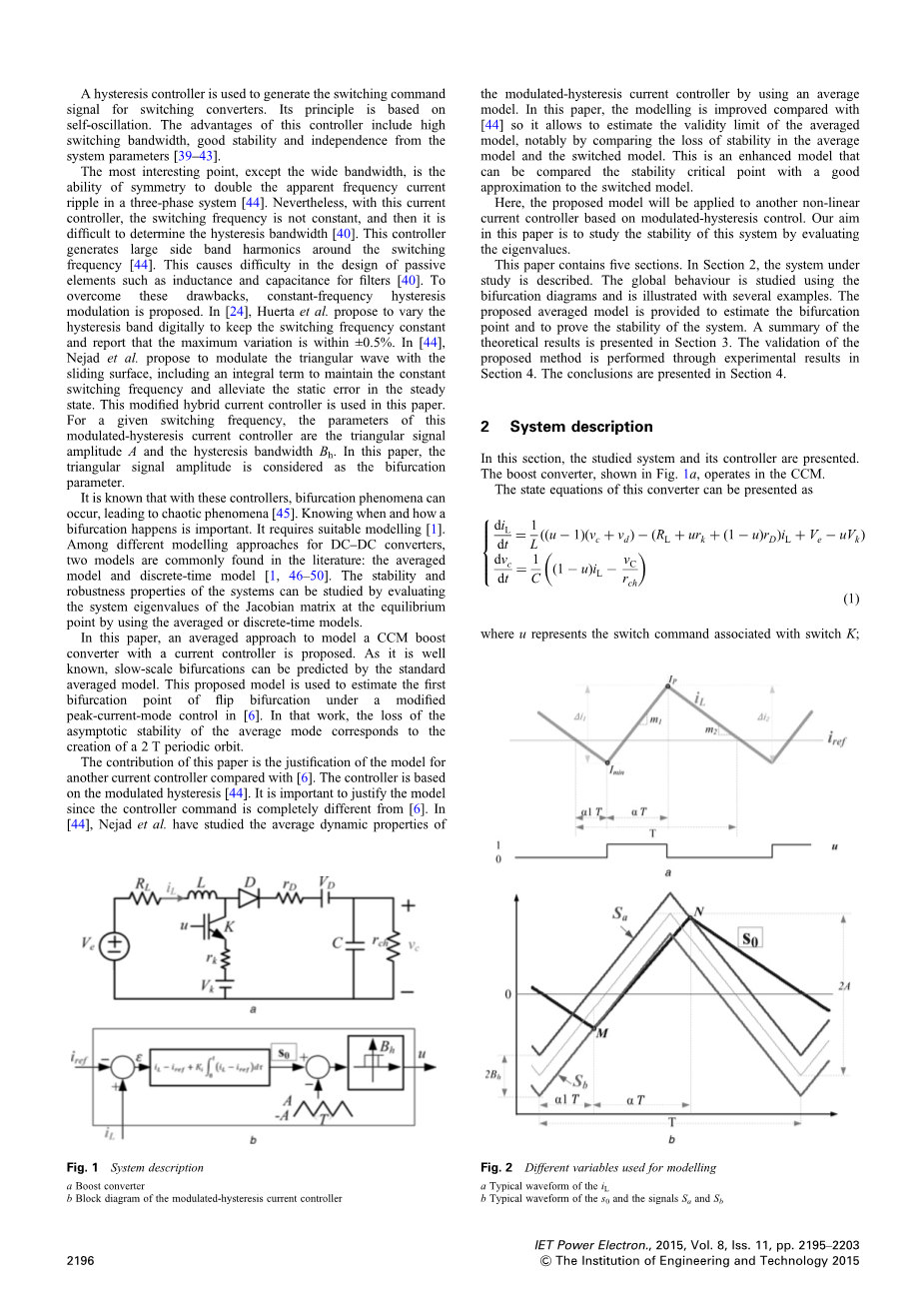
在本节中，介绍了研究的系统及其控制器。升压变化器工作于连续导通模式，如图1。

图 1 系统描述

升压变化器； 调至置换电流控制器框图

状态方程如下：

(1)

表示与开关管K有关的转换指令。

当，开关管导通；，开关管截止。，与分别为开关管，二极管与电感的寄生电阻。 为输入电压。与为与无关的，上的压降。负载电阻并联电容，为输出电压。为了简单起见，电感电流将在没有输出电压回路的情况下进行控制。对于电流回路，我们注意到 为两项之和：电流与参考电流之差以及其积分。

(2)

电流误差的积分项用于保证在稳定条件下无静差。为积分项的系数。确定了电流控制器的带宽。

混合调制-滞环控制器的运行模式在[44]中体现，优缺点也详细描述了。电流控制器框图见图1b。上述控制器输出信号，且此信号中混有三角载波，幅度周期对应于理想开关频率。得到的信号输入一个滞环调制器，用滞环带来产生控制信号，如图1与图2所示。

因此，为了模拟电流控制器，依靠占空比加上开关信号，项与电感电流得出了隐式方程

(3)

与对应的上下带如图2所示。这些信号会在3.2节详细说明。

图2 不同变量的模拟

的典型波形

信号，，的典型波形

3 稳定性分析

为了分析系统的动态性能提出了两种方法。

开关模型：通过使用电路仿真，分叉图可以获得。分岔点可以通过使用分叉图。它是一种方便的方式来表示进化作为参数的函数。这种方法证明了该系统的给定值的循环的稳定性控制参数。但是，要确保循环保持稳定在大范围的系统参数变化中，需要模型。

平均模型：可以通过估计系统特征值来获得分叉点。为了确保稳定的单周期循环，一个可能的解决方案是研究在稳定状态下评估的特征值的值

3.1 采用开关模型的稳定性分析

进行了两项实验，参数在表1中给出。

控制器的参数为三角波信号幅值（）与滞环环宽（）。幅值看做分岔参数。电感电流为每个开关周期初始稳态下对不同幅值的采样值。如果系统工作在周期-1，所有点将落在相同位置，并且每个参数值只能观测到一个点。分叉图如图3所示，实验1（顶部）和实验2（底部）。第一个实验中，分岔点发生在。当大于此值，可得到单周期循环。第二项实验中，在获得第一个分岔点。理想工作区标记于区域1。

图3 变化下的电感电流分岔图（上：实验1）（下：实验2）

如分岔图所示，随着三角信号幅值的减小，边界碰撞分岔从周期1态变化到多周期态。

为了更深入了解非线性特性，的临界值附近的时域仿真波形如图4与图5所示。

图4 两个值仿真下的电流波形（实验1）

图5 不同值的电流仿真波形（实验2）

电流在两个值的仿真波形在实验1中的图4显示。将的值(负载三角波幅值)设置为略大于系统稳定时的分岔点，另一个值则设置在略小于系统稳定时的分岔点。单周期性能可在区域Ⅰ中选取的获得。

在实验2中，用同样的方法进行仿真，图5显示了电流在的波形。该图能阐明当系统略高于以及略低于系统稳定时的分岔点状态下的特性。对于，出现多周期轨道的状态轨迹。如这些图所示，边界碰撞分岔点出现在分别从实验1中到周期1轨迹到周期7轨迹以及实验2中的周期1轨迹到周期3轨迹。

3.2 采用平均模型的稳定性分析

由于雅可比矩阵的特征值，能进行周期性质的研究。在这个部分中，详细说明了用于推导系统的雅可比矩阵所提出的方法。建模需要的变量在图2中列出，例如占空比（），在开关周期（ ）开始时的关断序列的持续时间，载波三角波振幅（），滞环带宽（）以及稳态模式下最大最小电流（）。假设系统时间常数远大于开关周期时间。

3.2.1 系统定义：DC/DC工作在连续导通模式。根据图1，状态矢量定义如下

(4)

表示状态变量在一个开关周期的平均值。状态矢量验证以下微分方程

(5)

此处为与开关管有关的占空比。

3.2.2 电流控制器模型：由图2可知，最大最小电流（）可以从几何学上计算出来。电流脉动

(6)

为了模拟电流控制器，与之前在（3）中提到的方法一样，一个与状态矢量，占空比以及项有关的隐式方程可如下定义

(7)

(8)

根据图6，积分项可以表示为两部分，也表明了如下的暂态和稳态性能

图6 暂态下的变化

和对于稳态没有影响。总之，这两个参数是补充量，但对于通过连续模型研究系统稳定性来说是必不可少的两项。

本文之前计算过补充项，指出了另一个控制器（峰值电流模式控制）的暂态。我们推导出

(9)

由式（6）与式（9）可知，能计算出如下与的值

信号与可用傅里叶形式表示

(10)

由式（5），（8），（9）与（11）可得函数。与在平衡点的值为式（8）当与时的解。

3.2.3 雅可比矩阵的计算

为了得到雅可比矩阵，考虑在该点周围具有小的扰动的工作点。式（5）的一阶化可得

（11）

然后

(12)

且。

式（5）中的并不取决于；因此.从而有

(13)

由式（7）中的关系可得出

(14)

(15)

最后两个方程消去并计算

(16)

将（16）代入（13）可得，

最终，可得出使用参数的雅可比矩阵

雅可比矩阵的特征值的计算可研究连续模型的稳定性。

知道雅可比矩阵的特征值可用于随着三角信号幅度变化时，识别分叉点从而研究系统在工作点附近的稳定性。平衡点处的特征值可从下式得出

(17)

在平衡点附近应用的特征值演变如图7所示，当随着之前实验1与实验2中的参数而改变。我们对特征值的轨迹的观察表明当变化时有不连续性。在实验1中，对于时的特征值实部为负。这与使用图3分岔图得到的分岔点相吻合。在实验2中，的临界值为2.21。通过图3所示的分叉图预测的结果对应于使用连续模型获得的结果。两个模型中存在小误差。所提出的平均模型对分叉值的有很好的估计。对于的值，特征值之一有正实部。它对应于系统的周期性特性的产生。因此，所提出的平均模型研究了由状态轨迹描述的极限循环的稳定性，并能对分叉值进行估计。

图 7 变量的特征值估计

3.2.4 鲁棒性分析

在这节中研究了电流控制器的鲁棒性。的值设置在4.5。详细参数见表1（实验1）。考虑电感与串联电阻的值在其标准值附近可能变化，如下

(18)

图8表明了电感和串联

剩余内容已隐藏，支付完成后下载完整资料

---

资料编号：[141804]，资料为PDF文档或Word文档，PDF文档可免费转换为Word