基于多目标模糊决策的分布式电源配电网重构

摘要 本文基于多目标迷糊决策提出含有分布式电源（DG）的配电网重构方法，实现放射状配电网的有功功率最小、电压幅值最大。考虑到馈线之间的负载平衡、有功功率损失最小、节点电压偏移和分支电流的限制等建立多目标方程，并且满足放射状网络中能给所有负载供电。这些目标方程是不精确评估每一个目标的模糊数学的集合。本文的创新之处在于采用多目标模糊优化方法对含有DG的配电网进行重构。算例为含DG的70节点配电网，基于多目标模糊优化法进构。仿真结果表明，通过此方法，有效降低了37.92%的有功损耗。

关键词：配电网重构，分布式电源，多目标优化，模糊逻辑

Ⅰ.引言

分布式电源（DG）多被定义为接入输电网或配电网的、容量小于10MW的小型发电机，多是可再生能源发电。随着人们对能源保护和环境问题的关注，可再生能源的需求日益增大，使得诸如燃料电池、太阳能发电、风力发电和其他形式的能源发电技术越来越受欢迎。印度尼西亚政府计划在2025年利用可再生能源发电的分布式电源上占到电网总容量的5%。大量研究证明，配电网中DG的接入对电网产生各种影响，其中电压升高是对农村配电网的主要影响。缓和其带来的不利影响的传统方法对开发者和配电网运营者来说都代价昂贵。随着配电网容纳DG水平的提高，规划和设计配电网将需要利用信息和通信技术手段，从而有效管理网络（例如，网络重构）。

电力配电系统通过开关来配置网络。系统中主要由两种开关的状态来决定配电网的配置，分别是联络开关和分段开关。网络重构是通过切换配电网节点的开关状态建立的。在现代电力配电系统中，多目标馈线重构问题意义重大。多目标是指在满足放射状结构网络中所有负载都有供电时，馈线之间的负载平衡和有功功率损失最小。人工或者自动开关操作时，其操作可能有所不同，因此配电网是在可能的最小线路损失下对负载供电的，从而提高系统可靠性和改善电能质量。重构也是在降低或者缓和馈线的过载问题。网络结构的改变是通过断开或闭合网络中的分段开关和联络开关。这些开关操作是在所有负载都有供电的情况下保持网络的放射状结构。

很多文献中研究者都聚焦于通过网络重构来降低网损。配电网重构旨在降低网损这一观点最早是由Merlin和Back提出来的。他们使用学科分支和限制类型的优化方法来确定最小损耗的重构。在这种方法中，所有的网络开关最初都是闭合的，来形成最多网孔的网络。随后相继断开开关保持辐射状网络结构。在这之后，出现了很多降低配电系统网损的算法。

Zhou 等人为配电网重构提出了两种算法，解决故障设备恢复和负载平衡问题。他们的优化方法中，为提高效率和强大的执行力而综合使用启发式规则和模糊逻辑。Taleski和Rajakovic提出了一种优化方法是对于给定的部分网络，在电能损耗最小的前提下进行确定网络配置。Borozan和Rajakovic考虑到了优化配电网重构中的应用方面。Lin和Chin基于电压指标、欧姆指数和决策指数提出了配电网重构的一种算法来确定开关操作。Joe和Augugliaro等人提出了人工智能方法在在最小损耗的配网重构方面的应用。Nara等人基于遗传算法（GA）提出了实现最小网损的配电网重构方法。

Das在优化配电网结构中基于模糊多目标方法提出了一种算法。建立这四个目标的模型：馈线之间的负载平衡、有功功率损耗、节点电压划分和分支电流限制。获得的结果是令人兴奋的，然而为每一个目标选择成员方程的标准没有确定。Rao等人提出了在大规模配电网中用于网络重构优化的和声搜索算法（HSA）。这一算法是由声乐中为达到最佳和谐状态而不断搜索的过程这样的观念演变而来。

在本文的研究中，配电网重构问题的规划是一个满足运行和电力条件情况下的多目标问题。在此讨论的规划方法主要考虑有关系统有功损失最小、节点电压偏移最小、分支电流过限最小和不同馈线之间负载平衡等四个不同的目标。重构之后要保持网络的辐射状结构，网络中所有的负载都能得到持续供电。这四个目标根据模糊集合建模。为使联络开关操作次数最小，启发式规则也结合使用到这个算法中。这个研究的目的是在说明模糊多目标算法在含DG的配电网重构问题中能够有效利用，使得系统有功损耗最小并且实现馈线之间的负载平衡。

Ⅱ.模糊多目标方法

本文中的模糊多目标方法是由Das发展而来的。在模糊系统领域内，每一个都和相应的成员方程相联系。这些方程反映对目标的满意程度。在精准的领域，满足或违背了目标，分别用函数值1或者0来表示。相反，模糊集合领域能够从0到1反映不同程度的成员方程函数值。因此，模糊集理论是标准集理论的扩展。当需要同时满足多个目标时，就需要在多个目标之间作出妥协以得到最好的解决方法。

本研究中的四个目标首先进行模糊化，然后将模糊化后的结果配以合适的权重整合成一个总的目标方程。在配电网重构问题中提出的这个方法，mLi、mVi、mAi和mBi分别表示有功损耗、最大节点电压偏移、最大分支电流负载指数和负载平衡的方程。成员值越大，则说明解决方法越优。下面描述的是模糊系统中的边界值高或者低的成员方程。

1. 有功损耗成员方程

这个方程的构造目的是为了降低有功损耗。我们有如下定义：

，for （1）

在这里，表示当第i个联络开关闭合时，包含联络开关的回路中的分支总数；是当回路中的第i个分支断开时辐射状结构系统中总的有功损失；是网络重构之前总的有功损耗。

从（1）式可以看出，当的值较大时，说明有功损耗降低得较少，因此成员值较小；反之，当的值较小时，有功损耗降低得比较多，相应的成员值就较大。

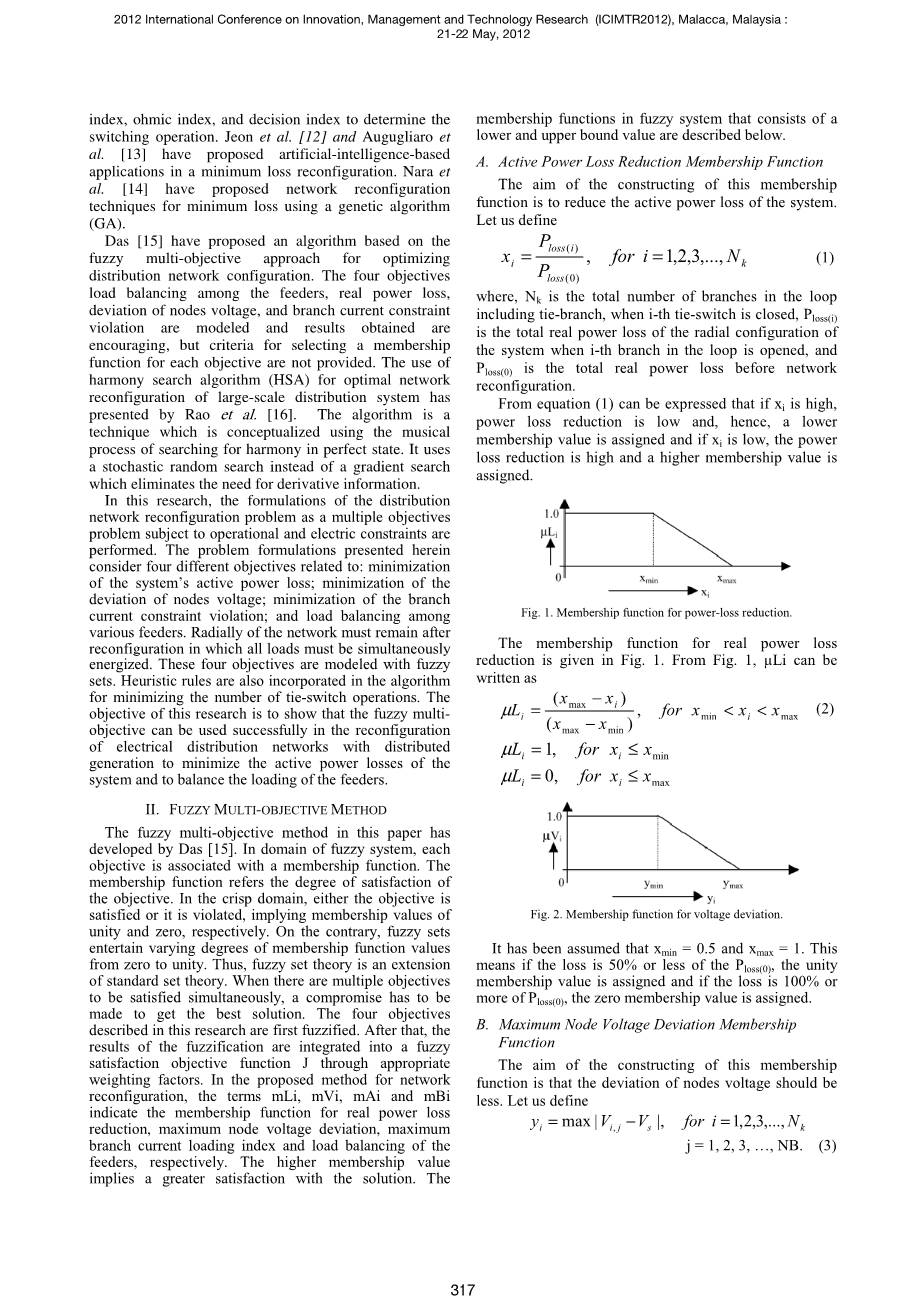
图1.降低有功损耗的成员方程

反映有功损耗降低的成员方程如图1所示。从图1可以看出，可以表示表示如下：

，for (2)

，for

, for

这里假设和。这意味着当有功损耗是的50%或者更少时，成员值为1。当损失是的100%或者更多时，成员值为0。

1. 最大节点电压偏移成员方程

这个成员方程构造的目的是使节点电压偏移最小。定义如下：

，for

. (3)

这里是当第i个联络开关闭合时包含联络开关的回路中的分支总数；NB是系统的节点总数；是每个变电站的电压；是相应的回路中第i个分支的节点电压。

图2.电压偏移的成员方程

在模糊研究中，若最大电压偏移较小，则相应的成员值较高；反之偏移越大，成员值越低。图2表示最大节点电压偏移的成员方程。由图2我们可得，

，for （4）

，for

，for

在本文中，我们假设和。意味着变电站电压标幺值为1时，最小系统电压的标幺值为0.95；当最小系统电压标幺值大于等于0.95时，成员值为1。类似的，当时最小系统电压标幺值为0.90，当其小于等于0.90时成员值为0。

1. 最大分支电流负载系数成员方程

此方程的基本目标是使分支电流越线最小。有以下定义：

分支电流负载系数= （5），for 。

这里是当第i个联络开关闭合时包含联络开关的回路中的分支总数。是当回路中第i个分支断开时第m个分支的电流幅值；是第m个分支的线路容量；NB是系统的节点总数。定义如下：

，for 和

当分支电流负载指数超过1时，成员值较小；只要指数值小于等于1，成员值就最大（例如为1）。最大分支负载指数的成员方程如图3所示，我们可得到：

，for (7)

,for

,for

图3.分支电流负载系数成员方程

在这种情况下，假设和。表示只要系统的分支电流小于等于各自的线路容量，则成员值为1。表示在每个分支里允许15%的过载，若在任何分支里电流大于等于线路容量的1.15倍，则成员值为0。

1. 馈线负载平衡成员方程

负载平衡是馈线重构的主要目标之一。增加配电网中负荷较重的馈线的负荷极限就是将其部分负荷转移到负荷较轻的馈线上。馈线平衡负载指数可以如下定义：

，for 和 （8）

是第i个联络开关闭合时包含联络开关的回路中的分支总数；NF是馈线总数；是当回路中第i个分支断开时第j条馈线上的电流；是当回路中第i个分支断开时所有馈线中电流的最大值，即，for 。

图4.负载平衡指数成员方程

我们定义 ，for 和 （9）

1. 式表明如果的值较小则可以实现较好的负载平衡。因此，值越小，成员值越高；反之成员值越低。图4表示了的成员值：

，for （10）

，for

for

在这种情况下，假设和。表示当馈线电流最大时电流偏移量最大为10%。如果偏移量小于等于10%，则成员值为1。表示当偏移大于50%时成员值为0。

1. 模糊多目标的算

重构算法如图5所示。

开始

读入系统数据

输出结果

结束

？

输出结果

I从1到分别计算和，

确定

选择联络开关k并确定

赋值

计算当时的

运行负载潮流计算程序

No

Yes

图5.网络重构算法流程图

Ⅲ.实验结果

为了展示所描述的方法的效果，我们测试了11kV的放射状配电网，如图6所示。该配电网包含两个变电站、四条母线、70个节点和78条分支。 该网络的两个变电站在拓扑结构上由两个分配节点所连接。这个系统的联络开关在正常情况下是断开的。图6展示的是无DG的配电网的最初配置。基于模糊多目标方法对含DG的配电网进行重构优化是在Matlab软件上实现的，仿真的实现条件是：1.8GHz,4GB的RAM的Intel酷睿二代微处理器。

在网络重构之前，系统的整个有功损失是227.510kW。如图7所示，母线上出现的最小的电压幅值是在节点67上，其标幺值为0.9。在本文中。我们在编号为3、6、24、29、38、52和64共7个节点上分别安装一分布式电源，如表1所示。从70节点的网络算例研究的结果可以看出，在特定的算例中分布式电源能有效降低馈线上网损。如表2所示，含DG的系统中总的有功损失是156.206kW，或者说总的网损降低了31.34%。如图8所示，节点67上的最小的电压幅值的标幺值是0.913。

表1.分布式电源的容量和安装节点

图6. 11kV放射状网络系统

网络重构之后，如表2所示，总的有功损失为141.239kW。或者换句话说，有功损失降落了37.92%。最小的电压幅值出现在节点15上，其标幺值为0.937。图9展示了含DG的配电网重构之后每个节点的电压幅值图像。

图10和图11分别是配电网重构前后每个节点的有功损耗分配。可以看出几乎每个分支的损耗都降低了，除了节点4、6、7、11、16、18、19和20的损耗上升了因为有负载转移到这些馈线上。

图7.不含DG的配电网重构之前每个节点的电压

图8.含DG的配电网重构之前每个节点的电压

图9.含DG的配电网重构之后每个节点的电压

从算例研究结果可以看出，含70节点的放射状网络中，在一些情况下分布式电源有降低网络损耗的作用。并且不含DG与含有DG的配电网重构优化后的拓扑结构是不一样的。

表2. 70个节点配电网的仿真结果

图10. 重构之前的有功损耗分配

图11. 重构之后的有功损耗分配

基于含DG的70节点放射状网络，本文中所展示的方法对降低网损有显著效果，从而可以改善含DG的配电网的效率。本文的方法没有和其他方法相比较，因为就作者来看，对于含DG的70节点配电网没有其他类似合适的方法来做对比。

Ⅳ.结论

本文提出了一种有效的方法对含DG的配电网进行重构优化。通过对70节点配电网的测试研究证明了这种方法的有效性。这种方法的主要优势在于降低配电网的有功损耗、提高节点电压的幅值从本文的研究结果可以看出，分布式电源对降低网损有改善作用，而且可以提高配电系统的电压幅值。在含DG的配电网中，相比于没有优化时降低了31.34%的网损，通过模糊多目标优化方法可以实现降低37.92%的网损。

致谢

作者衷心感谢印度尼西亚的高等教育总署（DIKTI）、文化和教育部资助此项研究。竞争研究资金的合同号为：560.5/K5/KL/2012。同时

剩余内容已隐藏，支付完成后下载完整资料

---

英语原文共 6 页，剩余内容已隐藏，支付完成后下载完整资料

---

资料编号：[140414]，资料为PDF文档或Word文档，PDF文档可免费转换为Word