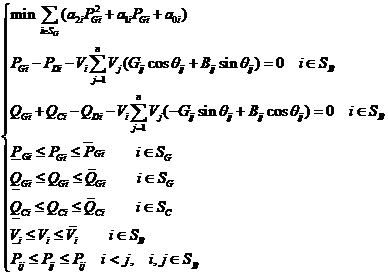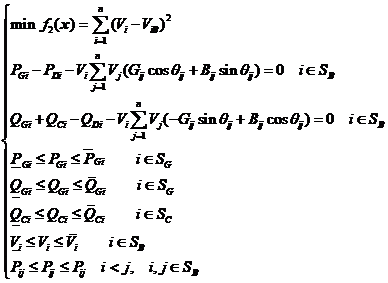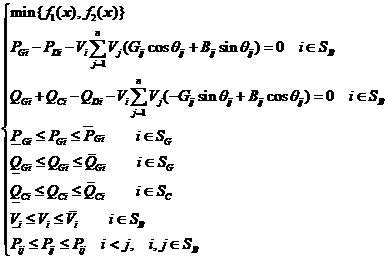基于发电成本和电压质量的最优潮流研究与设计毕业论文
2020-02-18 10:50:48
摘 要
电力系统的潮流计算是电力系统分析中的一种最为基本且最为重要的计算,对给定的运行条件确定电力系统的运行状态是潮流计算的任务,潮流计算已在电网经济调度、无功优化、电压调控等领域广泛应用。但目前现代电力系统的最优潮流模型具有非线性、非凸性、维数高、变量多(节点多)和求解难度大等问题。针对现代电力系统的特点,本文建立基于发电成本和电压质量的多目标最优潮流模型,研究与设计先进的求解方法,克服在求解最优潮流模型的算法中,经典算法容易收敛于局部最优解,现代智能算法花费的CPU计算时间长的缺点。
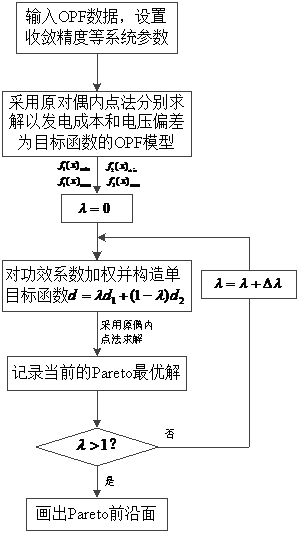
本文详细阐述了基于发电成本和电压质量的最优潮流研究与设计这个课题的目的和意义,介绍了国内外多目标潮流计算的研究现状。在分析了多种潮流计算模型的优点和缺点后,选择原对偶内点法求解最优潮流计算模型,详细介绍了原对偶内点法的计算原理和计算步骤。然后分析了目前常用的几种多目标优化算法及其优缺点,并选择功效系数加权法算法求解多目标优化问题。最终建立基于发电成本和电压质量的多目标最优潮流计算模型。
最后,以IEEE30节点标准系统为例进行仿真,构建基于发电成本和电压质量的多目标最优潮流计算模型,验证多目标最优潮流计算模型的有效性。最终仿真结果表明建立的多目标最优潮流计算模型能有效地实现电力系统的发电成本和电压质量的综合最优。
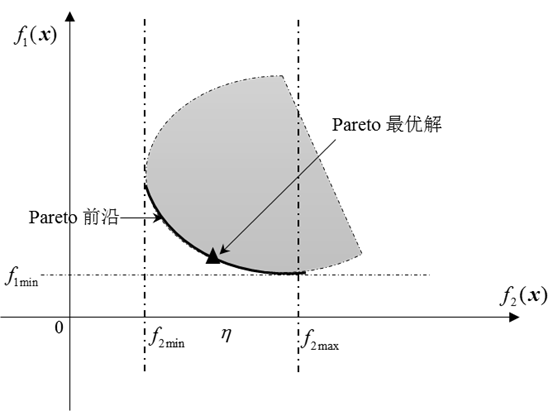
关键词:潮流计算,原对偶内点法,多目标规化,Pareto最优解,多目标最优潮流
ABSTRACT
The power flow calculation of power system is one of the most basic and most important calculations in power system analysis. It is the task of power flow calculation to determine the operating state of power system for given operating conditions. Power flow calculation has been widely used in power grid economic dispatch, no power optimization, voltage regulation, etc. However, since the Optimal Power Flow model in modern Power System presents features of non-linearity, non-convexity, high dimension and large scale of variables (that is large numbers of buses) and other bad properties, it is difficult to be dealt with. Aiming at the characteristics of modern power system, this paper establishes a multi-objective optimal power flow model based on power generation cost and voltage quality, researches and designs advanced solving methods, and overcomes the problem of solving the optimal power flow model. The classical algorithm is easy to converge to local optimum. and the shortcomings of CPU calculation time spent by modern intelligent algorithms.
This paper elaborates the purpose and significance of the research and design of optimal power flow based on power generation cost and voltage quality, and introduces the research status of multi-objective power flow calculation at home and abroad. After analyzing the advantages and disadvantages of various power flow calculation models, the original dual interior point method is selected to solve the optimal power flow calculation model, and the calculation principle and calculation steps of the original dual interior point method are introduced in detail. Then it analyzes several commonly used multi-objective optimization algorithms and their advantages and disadvantages, and chooses the efficiency coefficient weighting algorithm to solve multi-objective optimization problems. Finally, a multi-objective optimal power flow calculation model based on power generation cost and voltage quality is established.
Finally, the IEEE30-node standard system is used as an example to construct a multi-objective optimal power flow calculation model based on power generation cost and voltage quality to verify the effectiveness of the multi-objective optimal power flow calculation model. The final simulation results show that the established multi-objective optimal power flow calculation model can effectively realize the comprehensive optimization of power generation cost and voltage quality of the power system.
Keyword: Power flow calculation, Primal dual interior point method, Multi-objective programming, Pareto optimum, Multi-objective optimal power flow
目录
摘要 I
目录 III
第1章 绪论 1
1.1 多目标最优潮流计算的目的和意义 1
1.2 多目标最优潮流计算的研究现状 2
1.2.1 最优潮流计算研究现状 2
1.2.2 多目标优化算法研究现状 3
1.2.3 电力系统多目标最优潮流计算模型的研究现状 3
1.3 本文的主要工作 4
第2章 电力系统最优潮流计算 5
2.1 电力系统的潮流计算 5
2.1.1 电力系统潮流计算概述 5
2.1.2 电力系统潮流计算的数学模型 5
2.1.3 牛顿—拉夫逊法潮流计算 6
2.2 电力系统最优潮流计算 8
2.2.1 电力系统最优潮流计算概述 8
2.2.2 电力系统最优潮流计算与潮流计算的异同 9
2.2.3 电力系统最优潮流的数学模型 9
2.3.4 电力系统最优潮流计算算法 9
2.3 原对偶内点法 10
2.3.1 原对偶内点法概述 10
2.3.2 原对偶内点法的基础知识 11
2.3.3 原对偶内点法算法原理 12
2.3.4 原对偶内点法算法步骤 15
2.4 本章小结 16
第3章 多目标优化 18
3.1 多目标优化概述 18
3.1.1 多目标优化定义 18
3.1.2 多目标优化的基础知识 18
3.2 多目标优化算法 19
3.3 功效系数加权法 21
3.4 本章小结 21
第4章 电力系统多目标最优潮流计算 23
4.1 电力系统多目标最优潮流计算模型 23
4.1.1 目标函数 23
4.1.2 等式约束条件 23
4.1.3 不等式约束条件 24
4.1.4 单目标最优潮流模型 24
4.1.5 多目标最优潮流模型 25
4.2 电力系统多目标最优潮流计算算法 26
4.3 本章小结 26
第5章 算例分析 28
5.1 IEEE 30节点标准系统参数 28
5.2 单目标最优潮流计算的算例结果 29
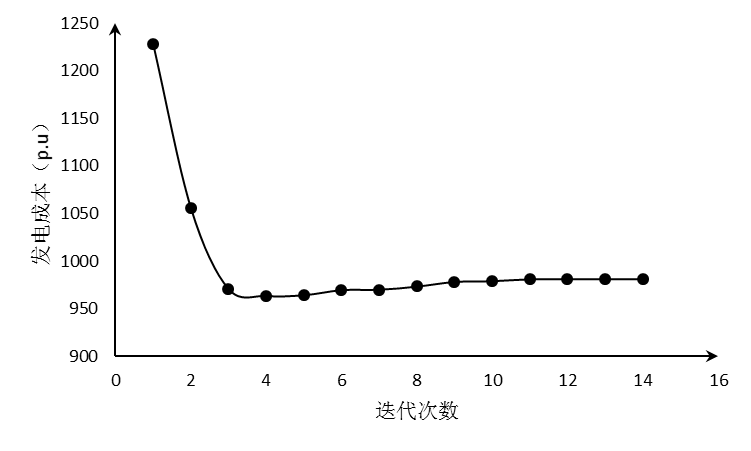
5.2.1 以发电成本为单目标函数的最优潮流计算 29
5.2.2 以电压偏差为单目标函数的最优潮流计算 30
5.3 多目标最优潮流计算的算例结果 31
5.3.1 功效系数加权法优化结果 31
5.3.2 理想点法求解Pareto最优解集中的最优点 33
5.4 算例结果分析 34
5.5 本章小结 34
第6章 结论与展望 36
6.1结论 36
6.2展望 36
参考文献 38
致谢 40
附录A IEEE 30节点标准试验系统数据 41
第1章 绪论
1.1 多目标最优潮流计算的目的和意义
电能是我们当今社会中最为重要、也是最为便利的能源。电能具有很多优点,电能可以方便容易地转化为其它形式的能量;它的输送和分配也很容易实现,可以实现远距离使用;它的应用范围广泛,规模也十分灵活。因此,在我们的日常生活中,电能是不可或缺的,它被及其广泛的应用在各行各业。提高现代社会的电气化程度,让电能替代其他形式的能量,是节约总能源的一个重要方法途径。
电能的生产、输送、分配和消费的各个环节组成的一个整体称为电力系统[1]。电力系统的运行具有十分明显的特点:电能无法大量存储;电力系统的两种运行状态的过渡十分迅速;电力系统在我们的日常生活中是不可或缺的。因此对电力系统的运行有着基本的要求:保证安全可靠地发、供电;要有符合要求的电能质量;要有良好的经济性;尽可能减小对生态环境造成的有害影响[2]。
符合要求的电能质量是电力系统运行的重要要求之一。衡量电能质量的两个基本指标是电压和频率,我国制定了额定电压和频率以及允许的偏移范围,当电压和频率超出允许的偏移范围时,会有很大的危害,此时用电设备的安全不能得到保证,严重情况下还有可能会危及到整个电力系统的安全运行。其中电压主要取决于电力系统中的无功功率平衡,当无功功率不足时,电压就偏低。因此,要保证良好的电压质量,关键在于系统发出的无功功率要满足功率平衡要求,要有配置得当的电源,还要有合适的调整手段。
良好的经济性亦是电力系统运行的重要要求之一。提高电力系统运行的经济性的方法就是必须尽量的降低发电成本和电力网的损耗率。发电成本主要体现在煤的损耗率,降低煤耗的主要手段是经济调度,可以通过增加低成本机组出力,减少高成本机组出力来实现。电能传输产生的损耗直接体现为电能的损失,大量的损耗不利于系统的经济运行,损耗可以通过无功补偿、调节变压器抽头位置、调节发电机的励磁来减少无功的流动,从而降低系统的网络损耗。减少损耗、提高效率,提高电力系统经济性。
电网规模一天天扩大、越来越复杂的电网运行方式和调度难度的增加是现代电力系统运行和控制的巨大挑战。作为优化无功功率和电压调节的主要目标的传统且成本有效的分配已经变得难以适应基于经济考虑的现有大型网络,同时考虑到安全要求,迫切需要开发网络优化,规划和监管的新业务和分析方法。潮流计算是电力系统分析中的一种最基本的计算,起源于上世纪60年代的最优潮流计算是现在电力系统最为重要的分析计算,所谓最优潮流,也就是说,当确定供应系统的结构参数和负载条件时,控制变量的优化,我们找到满足所有指定约束的能量流的分布并优化一个或多个系统性能指标[3]。选出最优的方案,就是最优潮流计算的目的和意义。
把最优潮流计算与多目标优化结合起来,即把发电成本和电压质量同时作为目标进行多目标最优潮流计算,具有重大的意义,可以实现以往最优潮流计算达不到的目的,可以更好地提高电力系统的经济性,提高电力系统的稳定性,降低发电成本,减少损耗,提高效率,实现电力系统更好地优化。针对现代电力系统的最优潮流模型具有非线性、非凸性、维数高、变量多(节点多)求解难度大特点。建立基于发电成本和电压质量的多目标最优潮流模型,研究与设计先进的求解方法,克服在求解最优潮流模型的算法中,经典算法容易收敛于局部最优解,现代智能算法花费的CPU计算时间长的缺点。
1.2 多目标最优潮流计算的研究现状
1.2.1 最优潮流计算研究现状
电力系统最优潮流计算起源于上世纪即二十世纪六十年代,作为电力系统最基本最重要的分析计算公具之一的最优潮流计算,在近半个世纪得到了长远的发展,最优潮流计算已经在电网的经济调度、无功优化、电压调控等一些领域得到了推广和应用。然而不得不说的是,现代电力系统的最优潮流模型具有非线性、非凸性、计算维数偏高、变量多(节点多)而导致的计算量大,求解效率过低,求解难度大的问题特点,为了解决这些问题,无数前人做出了大量的贡献,取得了不少的成果,除了提出由于目标函数和约束条件不同而构成,应用范围不同的最优潮流数学模型之外,更大量的是从改善算法的收敛性能,通常做法是对一些约束条件以及电力系统的实际运行条件情况进行相应的简化,之后在开展进行最优潮流计算,以提高计算速度,提高优化求解效率等目的出发,提出了最优潮流计算的各种方法。
最优潮流计算的算法目前可以分为两大种类,第一种类就是古典传统算法,即以数值解法为基础的算法,第二种算法是近年来引进先进原理的算法,引入目前发展迅速的人工智能的概念。
以数值解法为基础的算法主要有牛顿法、内点法、非线性规划法、线性规划法、二次规划法和混合规划法等等,这类算法各自有他们自己的特点。牛顿法是以简化海森矩阵为基础,作为迭代步长,具有二阶收敛性。非线性规划算法,是在简化梯度法和罚函数法上延伸进化而来,经过人们的一系列改进进化,发展成为现在结合简化梯度法和拟牛顿法优化转移惩罚函数的算法[4]。二次规划算法,是由拉格朗日函数法,将非线性规划问题分解成几个子问题,从可行域外的点开始启动算法[5]。线性规划算法主要是用对偶线性规划技术与修正的单纯法相结合,它具有比非线性规划计算性能强的优点[6]。混合规划算法主要是把线性规划算法和二次规划算法结合起来,线性规划有不容易求解不可分离目标函数的缺点,二次规划却能克服这个缺点,二次规划的计算性能不足,线性规划能克服这个缺陷,两种算法相辅相成[7]。内点算法从最早的障碍参数法,到基于多面体中心的内点法,逐步发展,在Karmarkar[8]提出了一种新型的求解线性规划的内点算法之后,并将其在非线性规划方面推广,内点法被广泛使用。这些算法总体来说,计算速度相对较高,尽管难以管理与离散变量对象相关联的约束,但它表示适合于在线计算的特征。
以人工智能为基础的算法是伴随着计算机技术的发展而新兴起来的,这种类型的算法主要基于自然和生物学的某些特征和行为,以便在没有繁琐的计算机处理或数值计算的情况下处理问题。主要分类有模拟退火法、遗传算法、粒子群算法、混沌搜索法、人工免疫算法等[9]。运用计算机和人工智能算法来进行电力系统最优潮流计算,大大减轻了人的计算和数据处理。
1.2.2 多目标优化算法研究现状
多目标优化对于我们来说是在现实各个领域中都普遍存在的问题,是一个非常重要的研究课题。多目标规划虽然是数学规划的一个分支,但在我们的现实生话中,许多现实问题都具有多目标的特征,当一个问题具有许多目标约束条件时,每个目标都不可能同时达到最优,这时必须各有权重。但是,究竟要怎样给每个目标分配这样的权重,这已经成为人们研究的热点问题。
在过去的几十年中,从最开始运用古典运筹学来解决处理多目标规划问题,出现过许多种确定性或者是随机化方法。传统古典的多目标优化方法是将各目标整合成一个带正系数的单目标函数,单目标函数的系数由决策者决定,或者由优化方法自适应调整。常见的古典方法有加权法、约束法、目标规划法和极小极大法等。
伴随着现代电子计算机的快速发展,计算机的计算速度也得到了大幅度的提高,出现了越来越多的基于计算机人工智能的进化算法。自从Schaffer在1985年第一次提出设计向量估计遗传算法(VEGA算法)开始[10],人们开始关注多目标进化算法对多目标优化问题的应用求解,进化算法也开始应用在如何解决多目标问题。因此人们设计了许多,出现了许多有效实际的多目标优化算法。目前常用的多目标进化算法有向量评估遗传算法(VEGA),小生境Pareto遗传算法(NPGA),多目标遗传算法(MOGA),非劣分类遗传算法(NSGA),孟德尔多目标简单遗传算法(NMOSGA),强度Pareto进化算法(SPEA),Pareto存档进化策略(PAES)等[11]。
1.2.3 电力系统多目标最优潮流计算模型的研究现状
当前,通过查阅参考文献,国内外在电力系统多目标最优潮流计算模型研究上具有许多模型,列出如下几种多目标最优潮流计算模型:
文献[12]是以发电费用和无功网损为目标,建立多目标最优潮流计算模型,主要考虑的是电力系统的经济性。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: