基于PPR势能内聚力法则的二次界面单元的开发与验证毕业论文
2020-04-05 10:59:34
摘 要
随着工程材料的多样性发展以及各个领域的交叉渗透,传统的断裂力学理论在处理界面粘结力学问题时暴露出了一定的不足,于是有学者提出了以界面粘结层间张力-位移法则为核心思想的内聚力区模型。经过近十多年的发展,该模型已被不断完善并广泛应用于研究各种粘结结构的裂纹尖端塑性变形以及各种新型复合材料的界面开裂问题。同时,随着计算机性能不断提高,人们也越来越倾向于将有限元法与内聚力理论相结合,从数值分析的角度实现对诸多界面脱粘或开裂问题的模拟研究。然而由于实际问题的复杂性,当前的商业软件中所包含的内聚力模型与材料属性仍无法满足相关需求,因此有必要利用商业软件提供的二次开发平台,开发出特定的内聚力界面单元计算模块。
本文的研究目标是在ABAQUS有限元软件中,建立基于PPR势能内聚力模型的二维二次零厚度界面粘结用户单元,主要的相关工作包括:1. 基于有限元基本理论推导二次界面单元的数值格式,并选择PPR势能的张力位移法则及卸载/重新加载准则作为此界面单元的本构模型;2. 基于ABAQUS提供的二次开发平台开发用户单元子程序,并利用单向拉伸和纯剪切两个简单算例对其进行调试和验证,通过与现有的PPR线性单元模型进行对比,评估程序的准确性和可靠性;3. 建立颗粒增强复合材料的有限元模型,将所开发的界面粘结单元插入到基体/颗粒的界面中,对其界面粘结力学响应进行了模拟,从数值分析的角度初步考察了颗粒和基体之间因界面脱粘出现的“空穴”现象。
关键词:界面单元;内聚力区模型;ABAQUS;用户单元子程序
Abstract
With the development of diversity of engineering materials and cross-infiltration in various fields, the traditional fracture mechanics theory has exposed certain deficiencies when dealing with interfacial bonding mechanics problems. Therefore, some scholars have proposed an interfacial bonding layer tension-displacement rule. The core idea is the cohesive area model. After nearly ten years of development, the model has been continuously improved and widely applied to the study of crack tip plastic deformation of various bond structures and interface cracking of various new composite materials. At the same time, with the continuous improvement of computer performance, people are more and more inclined to combine the finite element method with the cohesion theory, from the perspective of numerical analysis to achieve a number of interface debonding or cracking simulation studies. However, due to the complexity of practical problems, the cohesive force model and material properties contained in the current commercial software still cannot meet the related requirements. Therefore, it is necessary to use the secondary development platform provided by commercial software to develop a specific cohesive interface unit calculation module.
The goal of this paper is to establish a two-dimensional second-order zero-thickness interface bonding user unit based on the PPR potential energy cohesion model in ABAQUS finite element software. The main related work includes: 1. Derivation of the secondary interface unit based on the basic theory of finite element. Numerical format, and select the tension displacement rule and unload/reload criterion of PPR potential as the constitutive model of this interface unit; 2. Develop user unit subroutine based on the secondary development platform provided by ABAQUS, and use uniaxial tension and purity Two simple examples of shearing are used for debugging and verification. The accuracy and reliability of the program are evaluated by comparing with the existing PPR linear element model. 3. The finite element model of the particle reinforced composite material is established and will be developed. The interfacial adhesion unit was inserted into the matrix/particle interface and the interfacial adhesion mechanical response was simulated. From the perspective of numerical analysis, the “cavitation” phenomenon between the particles and the matrix due to interface debonding was initially investigated.
Keyword :interface cohesive element ;cohesive zone model ;ABAQUS;user-defined element
目录
第一章 绪论 1
1.1 研究背景及意义 1
1.2 内聚力模型的相关研究进展 1
1.2.1 内聚力模型的张力-位移关系 1
1.2.2 有限元计算中的内聚力界面单元 4
1.3 本文工作 5
第二章 内聚力单元的数值实现 7
2.1 内聚力区模型的基础理论 7
2.1.1 基于势能的PPR内聚力模型 7
2.1.2 卸载/重新加载关系 9
2.2 基于PPR模型的界面粘结单元 10
2.2.1 有限元法的基本理论 11
2.2.2 二维二次界面粘结单元的数值格式 12
2.2.3 内聚牵引力向量和切线矩阵 15
2.3 本章小结 17
第三章 界面粘结单元用户子程序的实现及验证 18
3.1 ABAQUS介绍 18
3.1.1 ABAQUS二次开发平台 18
3.1.2 ABAQUS中UEL用户单元子程序结构 18
3.1.3 UEL子程序中的主要变量说明 19
3.2程序实现 20
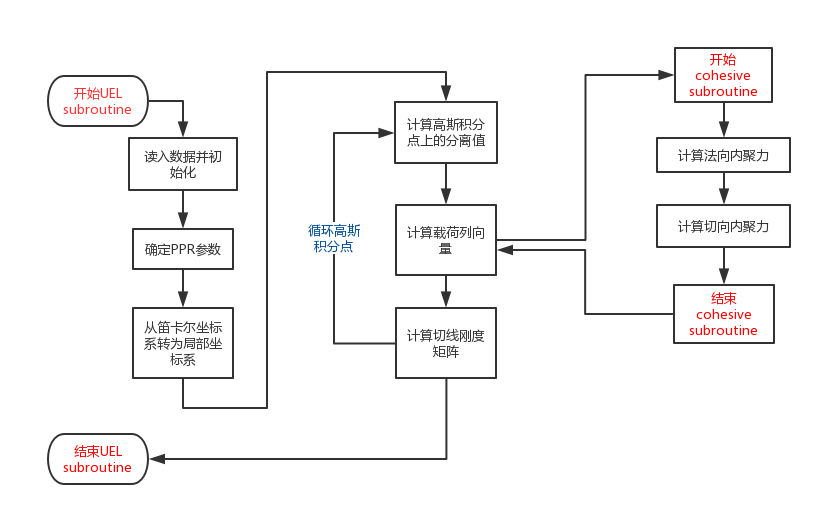
3.2.1 内聚力模型的UEL程序流程与结构设计 20
3.2.2 子程序的编写 22
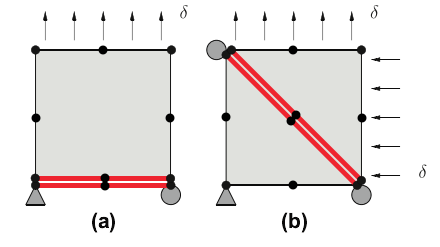
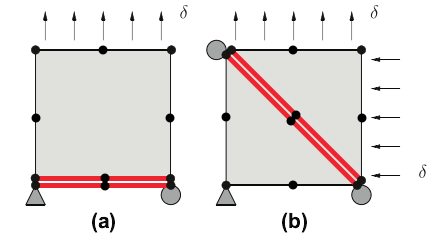
3.3 利用简单算例进行程序验证 26
3.3.1 单向拉伸算例:mode1 27
3.3.2 纯剪切算例:mode2 27
3.3.3 子程序的单元测试与线性单元的比较 28
3.4 颗粒脱粘分析 29
3.5 本章小结 31
第四章 全文总结及展望 33
4.1 总结 33
4.2 展望 33
参考文献 35
致 谢 37
第一章 绪论
1.1 研究背景及意义
随着工程材料的多样性发展以及各个领域的交叉渗透,传统的断裂力学理论方法在求解新型复合材料、结构的粘结界面开裂问题时逐渐暴露出一些不足,如遭遇裂纹尖端应力奇异性、开裂过程中裂纹附近不可忽略的塑性区等问题[1-2]。基于这一背景,有学者依据弹塑性断裂力学理论提出了内聚力区模型(cohesive zone model),该方法立足于计算开裂过程中的内聚应力与能力,从而避免了传统线弹性断裂力学中的裂纹尖端应力奇异性,能够较有效的表征粘结界面受载荷作用时的损伤失效过程[3-5]。作为弹塑性断裂力学中的一个有力工具,自Barenblatt[6]和Dugdale[7]提出内聚力区模型的概念以来,该模型已被广泛应用于考察各种材料与结构内部的裂纹尖端塑性变形、静力或疲劳条件下的蠕变开裂,以及金属基、混凝土基、高聚物基和橡胶类高弹体复合材料的界面脱粘问题[8-13]。
由于计算机性能的不断提高和各种数值计算方法的进步,相比于传统的实验与理论分析方法,数值模拟手段在粘结界面力学问题的研究中发挥了越来越重要的作用,其应用也越来越广泛。目前,将有限元方法与内聚力区模型相结合,对复合材料粘结界面进行模拟研究,已逐渐成为该领域中的趋势[14]。从已有的文献报道来看,大多数工作都是基于商业化软件平台(如ABAQUS、ANSYS、MARC等),利用其中自带的内聚力计算模块来完成的。当然必须指出,现阶段的通用有限元软件在这方面能够提供的选择并不多,以ABAQUS为例,其单元和材料库中自带的内聚力相关的单元类型和材料模型,都还无法满足某些较为复杂(如大变形、非线性较强,应力集中明显)情形的模拟分析需求。因此,仍有必要对内聚力模型的相关理论进行持续探索,并将所得的新成果应用于有限元模拟计算,即基于ABAQUS的二次开发平台,利用用户自定义的扩展模块,将相应的内聚力单元或材料模型编译为用户子程序,从而在通用的有限元软件中实现特定的粘结界面力学问题的模拟计算[15]。
1.2 内聚力模型的相关研究进展
1.2.1 内聚力模型的张力-位移关系
如前所述,内聚力模型在处理断裂或界面开裂问题中相较于传统断裂力学的优势,在于其建立的界面两端的内聚应力-分离位移关系(traction-seperation,简称T-S关系)。采用内聚力区模型,既表征了界面的断裂行为,同时描述了界面应力场的分布特征,并且内聚应力-分离位移关系还给出了粘结区在加载过程中的损伤演化规律。从这个角度而言,内聚力模型的关键就在于张力-位移关系,而不同的内聚力区模型之间的区别,也主要体现在张力-位移关系的不同选择[2]。
在内聚力模型的研究发展过程中,针对不同材料与结构中界面粘结与损伤失效的具体情况,人们提出了各种形式的内聚力理论模型,即不同的内聚应力-位移关系。目前比较典型的有双线性、梯形、多项式和指数型的张力-位移关系,这些分离关系已被应用于各种韧性开裂、复合材料胶接脱层及粘结界面开裂的研究中[14],下面简要介绍这些经典的内聚力模型:
(1)双线性内聚力法则
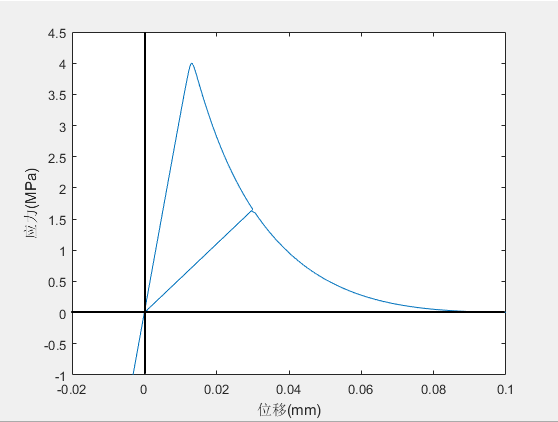
最初由Mi[16]等提出,是一种简单有效的内聚力法则,因其易于在有限元方法中实现,被许多商业有限元软件采用。模型在拉伸和剪切方向的T-S关系如图1.1所示,曲线的上升段和下降段均为线性:第一个阶段,内聚力区内应力随着界面相对位移的增大呈线性增长趋势;第二个阶段,内聚应力达到最大值(界面粘结强度)之后,界面区开始产生损伤,并逐渐失效,于是内聚应力随着分离位移的增加而呈线性下降,这意味着界面层承受载荷的能力减弱,该处裂纹逐步形成并扩展;最后,当分离位移达到最大值时,内聚应力减小至零,粘结区完全失去承载能力,该处裂纹完全扩展,内聚力界面单元发生破坏失效。
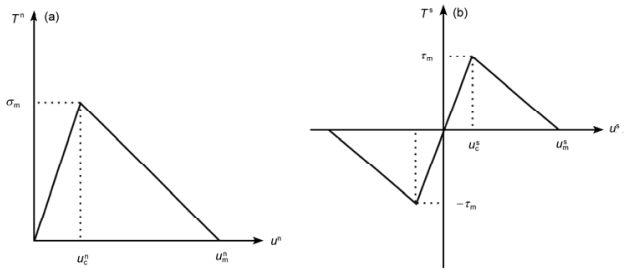
图1.1 双线性内聚力法则示意图
(2)梯形内聚力法则
第二种常见的内聚力模型由Tvergaard与Hutchinson[17]于1992年在研究弹塑性固体的开裂过程时提出,该法则也称为逐段线性张力位移法则。该模型的主要特点是将内聚应力-分离位移关系分成线弹性、理想塑性、线性软化三个阶段,如图1.2所示,这样便将界面T-S关系融入到界面开裂的塑性区域内,从而实现了经典断裂力学理论与内聚力模型的结合。
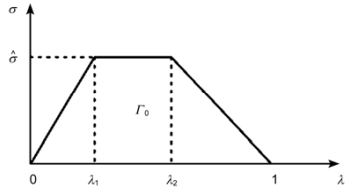
图1.2 梯形内聚力法则示意图
(3)指数和多项式内聚力法则
由Xu和Needleman[18]于1993年提出,采用了指数和多项式结合的形式来描述内聚力区的张力-位移关系。该模型是一种基于势函数的模型,用于描述内聚应力与分离位移关系的势能函数如下:
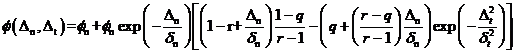 (1.1)
(1.1)
根据势函数,界面上的各向应力为:
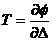 (1.2)
(1.2)
由此得到法向与切向界面粘结力与分离位移之间的关系如下:
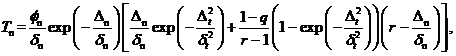 (1.3)
(1.3)
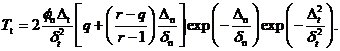 (1.4)
(1.4)
其中,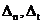 分别指内聚力单元表面上的法向和切向分离值,
分别指内聚力单元表面上的法向和切向分离值,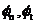 分别为纯法向、纯切向界面彻底开裂的界面断裂能,而式(1.1)计算的是整个开裂过程中的总断裂能。
分别为纯法向、纯切向界面彻底开裂的界面断裂能,而式(1.1)计算的是整个开裂过程中的总断裂能。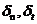 表示临界开裂位移,此时应力达最大值。而上式中参数
表示临界开裂位移,此时应力达最大值。而上式中参数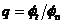 ,
,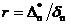 ,其中
,其中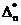 为当
为当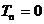 ,且切向彻底失效时的
,且切向彻底失效时的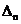 。Xu和Needleman利用此模型在统一的计算模式下,模拟了颗粒增强复合材料内部的界面裂纹萌生、发展直至颗粒/基体完全脱粘的全过程,并揭示出界面层的最大允许相对位移与脱粘的韧性和脆性关系[18]。这种内聚力法则的曲线如图1.3所示,相较于双线性模型及梯形模型等,它以势能为基准,对位移求导得到内聚力,保证了内聚力及其导数良好的连续性,目前被许多学者所采用。
。Xu和Needleman利用此模型在统一的计算模式下,模拟了颗粒增强复合材料内部的界面裂纹萌生、发展直至颗粒/基体完全脱粘的全过程,并揭示出界面层的最大允许相对位移与脱粘的韧性和脆性关系[18]。这种内聚力法则的曲线如图1.3所示,相较于双线性模型及梯形模型等,它以势能为基准,对位移求导得到内聚力,保证了内聚力及其导数良好的连续性,目前被许多学者所采用。
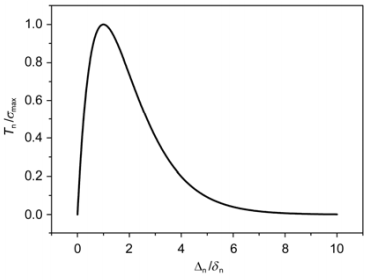
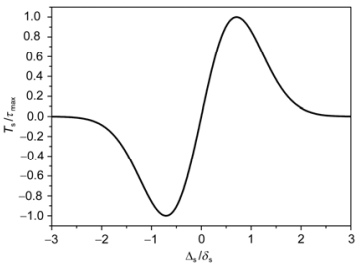
图1.3 多项式内聚力法则示意图
(4)基于PPR势能的内聚力法则
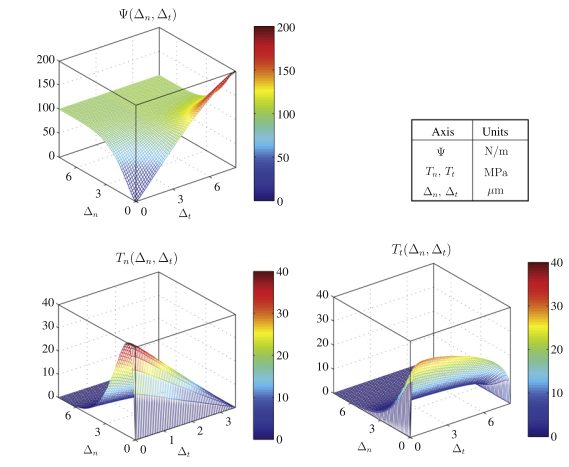
以上三种内聚力法则给出了三种较为常见的T-S关系曲线。然而,Paulino在最近的研究中指出,在混合模式的界面开裂过程中,现阶段的大多数张力-位移关系存在局限性,相应的选择也必须十分谨慎[19]。基于此,Paulino等提出了一个基于PPR势能的内聚力模型,相关的考察结果表明,这个新提出的PPR模型在混合条件以及考虑不同断裂能的断裂模式下都展现出较好的适应性。在PPR势能模型中,界面相互作用能被定义在一个内聚力相互作用区域内,如果界面分离达到了相互作用区域外,则内聚应力等于零,界面粘结失效。同时,鉴于该模型是在指数和多项式模型的基础上发展而来,其张力-位移关系及相关导数也都是连续函数,且法向和切向应力满足基本的对称性和反对称性要求,关于这一模型的具体细节会在2.1.1节中进行详述。
1.2.2 有限元计算中的内聚力界面单元
在现阶段的有限元计算细观力学中,主要使用与内聚力模型相对应的粘结界面单元(cohesive element)来表征多相材料内部的界面脱粘行为。如图1.2a 所示,界面单元通过在连续单元中间设置一对几何形状完全相同的面单元,来模拟两个实体单元之间的连接界面开裂的过程。在初始构型中,它的两个对应面完全重合(零厚度);但随着相邻实体单元的变形发展,它们之间有可能发生分离,即出现相对位移;同时内聚力及断裂能随着提前指定的张力位移法则也发生了变化,当内聚力最后减小至0时,界面粘结单元彻底破坏。通过这种方式来模拟实现界面两侧材料间的“脱粘”。在二维情况下,界面单元退化为两条相邻的线段(图 1.4(b))。
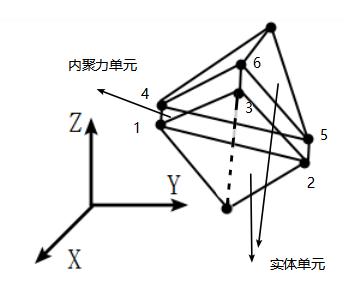
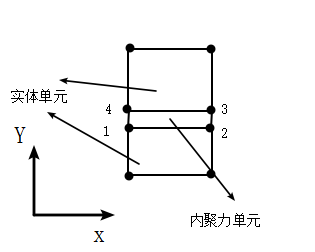
- 三维线性界面单元 (b) 二维线性界面单元
图1.4界面单元示意图
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: