摘 要

本文采用三点弯曲的实验方法测试了两种铺层的玻璃纤维增强树脂基复合材料（GFRP）和树脂基体在高温环境下的弯曲蠕变性能。基于时温等效原理，建立了GFRP复合材料的蠕变主曲线模型，并设计了包含时间和温度双变量的蠕变柔量函数。结果表明：利用活化能法求解转换因子适用于蠕变主曲线的建立，且蠕变主曲线能够预测复合材料长达50年的蠕变性能。基于复合材料的粘弹性质，采用四元件Burgers模型拟合GFRP复合材料高温下短期蠕变柔量，并由此得到复合材料的物理属性随温度变化规律。针对两种铺层的GFRP复合材料，采用不同的混合律模型，并通过实验结果研究其适用范围。结果显示：在较低温环境下和较短时间内，由于基体与纤维的界面相对完好，模型对复合材料蠕变是适用的。计算和对比了高温蠕变的必要分项系数，结果表明：树脂含量高的材料，其分项系数会略大于GB51160中理论值；纤维含量对分项系数影响较大。

关键词：GFRP复合材料；高温蠕变；时温等效原理；Burgers模型；蠕变混合律

Abstract

The bending creep behavior of glass fiber reinforced resin matrix composites (GFRP) with two different lays at elevated temperature was measured through three-point bending testing in this paper. Based on the principle of time-temperature superposition, the master curve of creep compliance of GFRP composites was built, and a function of creep compliance with time and temperature as variables was designed. The result shows that using the constant activation energy of the glass transition relaxation to estimate the shift factors is applicable to build the master curve, and the curve can be used to predict the creep level of GFRP composites at a end of proposed 50-year life. In view of the viscoelasticity of composites, Burgers model was applied to fit the short-term creep compliance of GFRP composites, and based on which characters of GFRP composites’ physical properties varying with temperature were summarized. For two kinds of GFRP composites with different lays, we adopted two models of creep mixtures respectively, and verified their applicability through the experimental results. The results show that, at comparatively low temperatures and within short-term time, the two models and calculating formulas are applicable to the creep of composites, for the interfaces between fibers and matrix kept comparatively intact. By calculating and comparing the necessary partial coefficients of creep at elevated temperature, we concluded that the partial coefficients of materials with high resin content were slightly larger than the standard one in the GB51160, and the resin content of composites have a great influence on the impartial coefficients that react to the change of temperature.

Key words: GFRP composites; elevated temperature creep; principle of time-temperature superposition; Burgers model; rule of creep mixtures

目 录

第1章 绪论 1

1.1 研究背景及意义 1

1.2 国内外研究现状 2

1.3 研究内容 3

第2章 GFRP复合材料高温蠕变实验 5

2.1 实验原理 5

2.2 试样制备 5

2.2.1 试样选材 5

2.2.2 试样参数 6

2.3 实验设备 6

2.4 实验方案 8

2.4.1实验设计 8

2.4.2实验步骤 8

第3章 蠕变理论模型与结果分析 9

3.1 GFRP复合材料长期蠕变主曲线模型 9

3.1.1 蠕变理论研究 9

3.1.2 时温等效原理 10

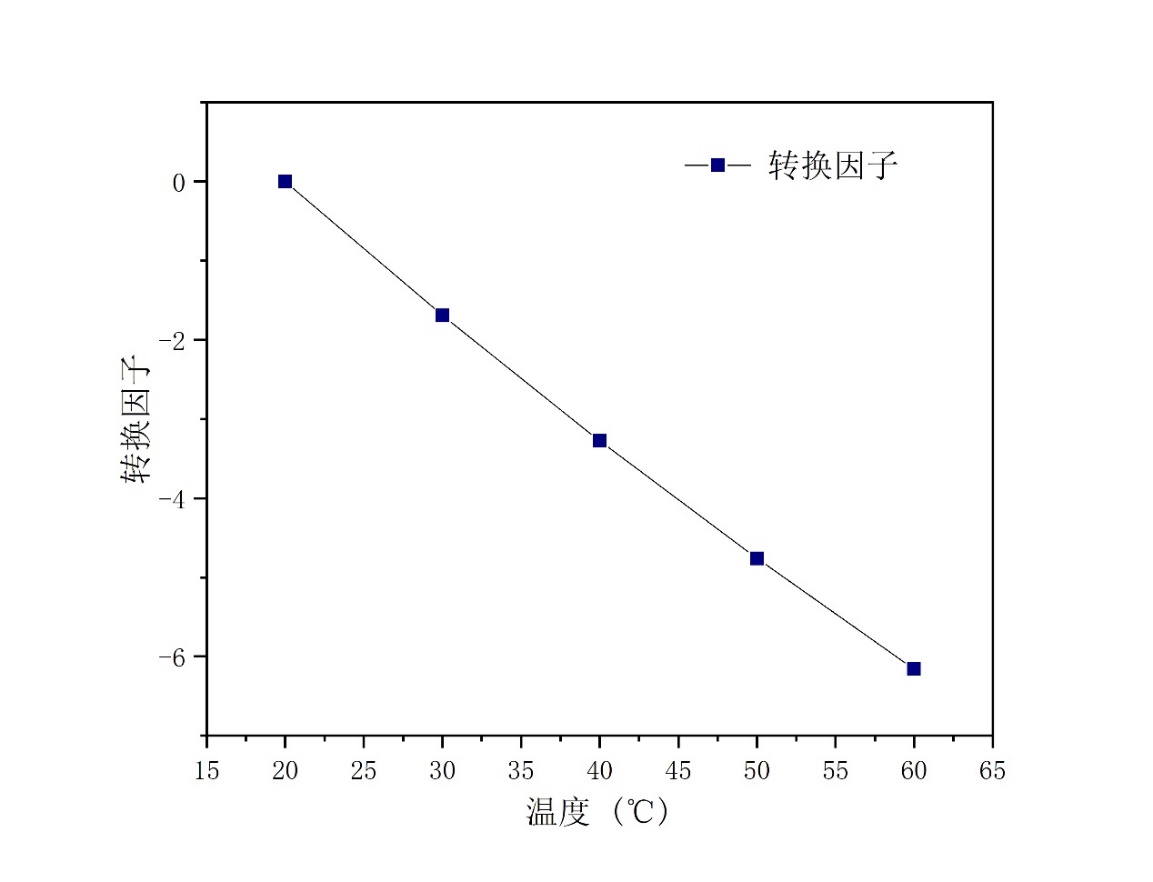
3.1.3 转换因子 10

3.1.4 主曲线的绘制 12

3.1.5 主曲线拟合 16

3.1.6 包含时间和温度双变量的蠕变数学模型 19

3.1.7 时温叠加主曲线与实际蠕变主曲线对比 20

3.2 GFRP复合材料短期蠕变Burgers模型 21

3.2.1 理论模型 21

3.2.2 Burgers模型曲线拟合 24

3.3 蠕变混合律模型 26

3.3.1 理论模型 26

3.3.2 数据处理与分析 28

3.4 GFRP复合材料必要分项系数的对比 31

3.4.1 分项系数的计算 31

3.4.2 数据对比与结果分析 33

第4章 总结与展望 35

4.1 总结 35

4.2 展望 35

参考文献 37

致谢 39

第1章 绪论

1.1 研究背景及意义

玻璃纤维增强塑料GFRP（Glass Fiber Reinforced Plastics）俗称玻璃钢，是以玻璃纤维作为增强相的树脂基复合材料，也是目前使用最为广泛的复合材料之一。目前，关于GFRP复合材料的制造生产工艺已经较为成熟，且在许多国家都已形成相关产业 ^[1]。

GFRP复合材料具有很多优点，包括：比强度和比模量大、耐疲劳性能好、轻质性、造价低、抗腐蚀、使用寿命长等，这些优点使得它在航空航天、船舶以及土木工程等领域都有广泛的用途^[2]。例如，材料的比强度和比模量是航空航天构件以及汽车、轮船等运输部件设计时所需考虑的重要指标。因此，比强度和比模量大决定了其可以制造出性能良好、重量轻的结构。研究表明，对于纤维增强复合材料，其疲劳强度极限能达到其拉伸强度的70%~80%，相比之下，金属材料只能达到30%~50%。因此，对于许多在长期交变荷载下的工程构件，复合材料相比其他材料具有较长的适用寿命和较大的破损安全性。随着时代的发展，以上优点使得复合材料可能成为传统工程材料（混凝土，钢铁，木材等等）的取代品之一^[3,4]。

当然，GFRP复合材料也有一些缺点，包括：弹性模量低、树脂基复合材料耐热性较低、属于脆性材料、材料性能分散性大等等^[5]。比如GFRP复合材料的弹性模量远不如钢材和大多数金属材料，因此在工程实践中，常常会因无法满足其刚度要求或是变形较大而不得不选用其他材料来代替玻璃钢。大多数增强纤维均为脆性材料，拉伸时的断裂应变较小，因此大多数纤维增强复合材料也为脆性材料，在纤维方向与垂直纤维方向都有不同程度的表现。在材料性能的分散性方面，有研究数据显示，通过手糊成型的玻璃纤维布增强复合材料，其强度离散系数可达到8%~10%，这在材料性能研究、规律总结以及理论检验方面都会有不同程度的影响^[1]。

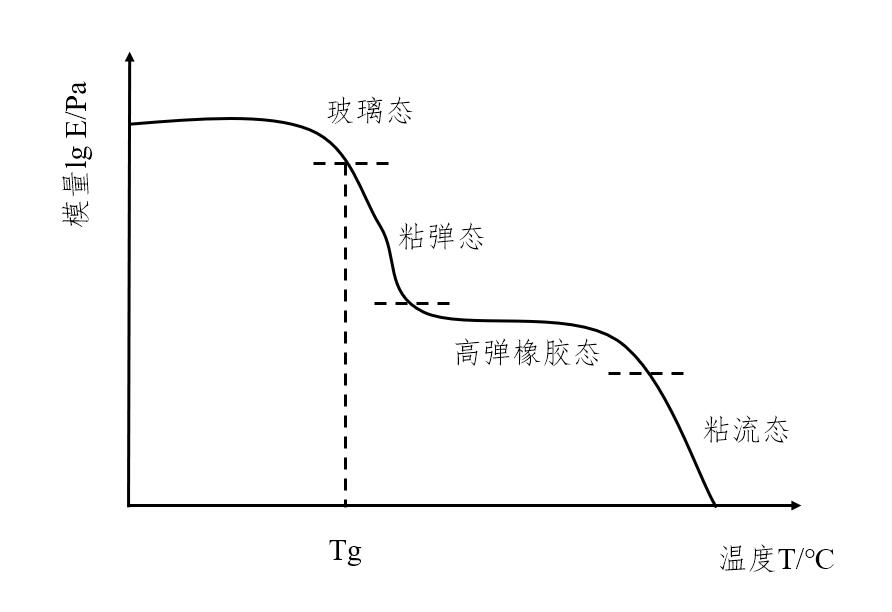
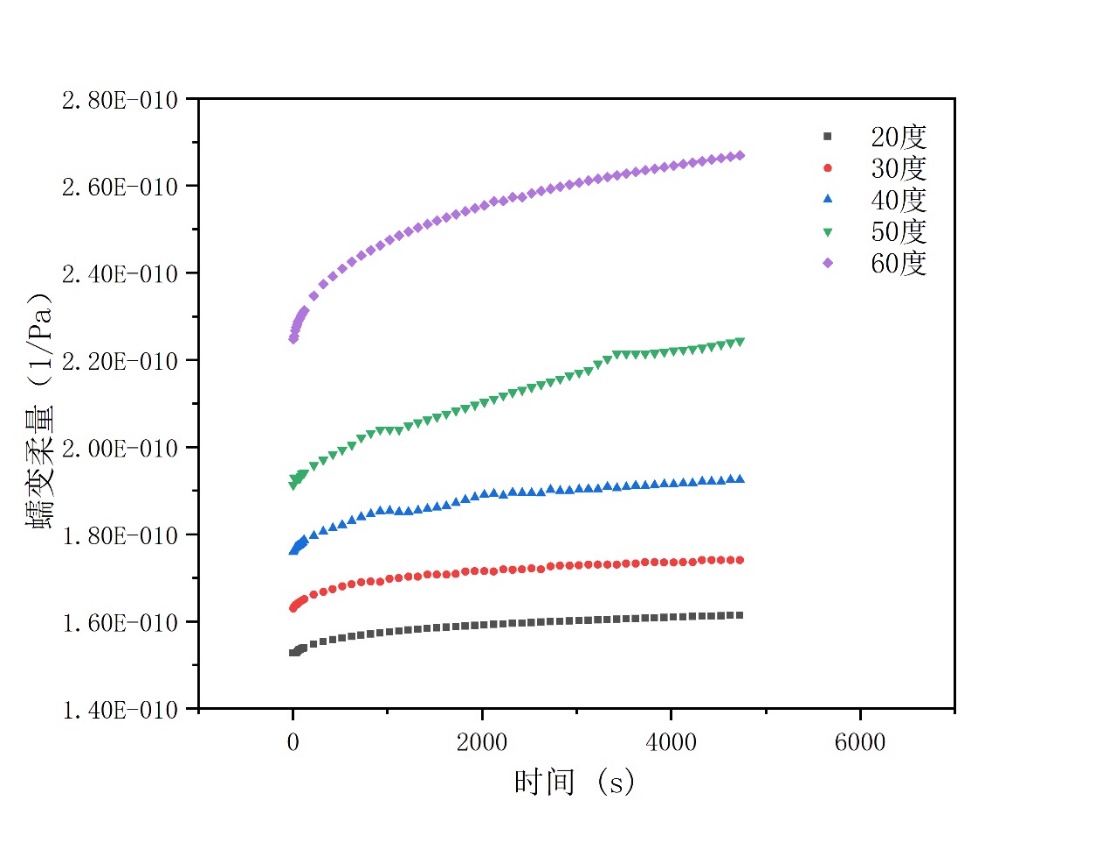
此外，树脂基复合材料最显著的缺点是在高温、常温甚至低温环境下长期服役过程就存在明显的蠕变或应力松弛现象。GFRP复合材料的强度和断裂荷载等力学性能会随服役时间的增加而下降，从而导致结构的失效破坏，因此GFRP复合材料的物理和力学性能的高温蠕变已经成为土木工程和建筑方面运用的主要担忧之一^[6]。高温会使复合材料发生玻璃化转变和树脂聚合物的分解，从微观角度来看，复合材料组分分子的活化能和自由体积都与温度密切相关，且随着温度的升高而增大。宏观上也会体现为材料的松弛时间减短和蠕变变形的增大^[7]。研究表明，随着温度的升高，GFRP复合材料的强度、刚度以及纤维和树脂间界面的结合程度均会下降。当材料温度在其玻璃化转变温度附近时，其力学性能会发生数量级的变化，从而导致材料失效。

因此，研究复合材料高温环境下的力学性能对于工程实际意义重大。通过对复合材料进行高温蠕变实验，可以得到其力学性能随时间、温度的变化规律。再结合已有的理论知识，对复合材料高温下蠕变性能进行模型化设计，归纳和总结，得出具有工程指导意义的结论与方案，从而提高该材料在建筑和其他领域的适用性和安全使用性。

此外，从细观力学角度对复合材料进行分析也有一定的现实意义。目前大多数复合材料的性能数据均通过实验获得，但试图通过实验测得所有材料组合的性能既不现实，也不可能。因此通过细观力学研究复合材料宏观性能与组分材料、细观结构之间的关系，再利用实验数据进行检验和校核，能够为进一步改善材料性能、进行材料设计和改进制造工艺提供指导性意见。

1.2 国内外研究现状

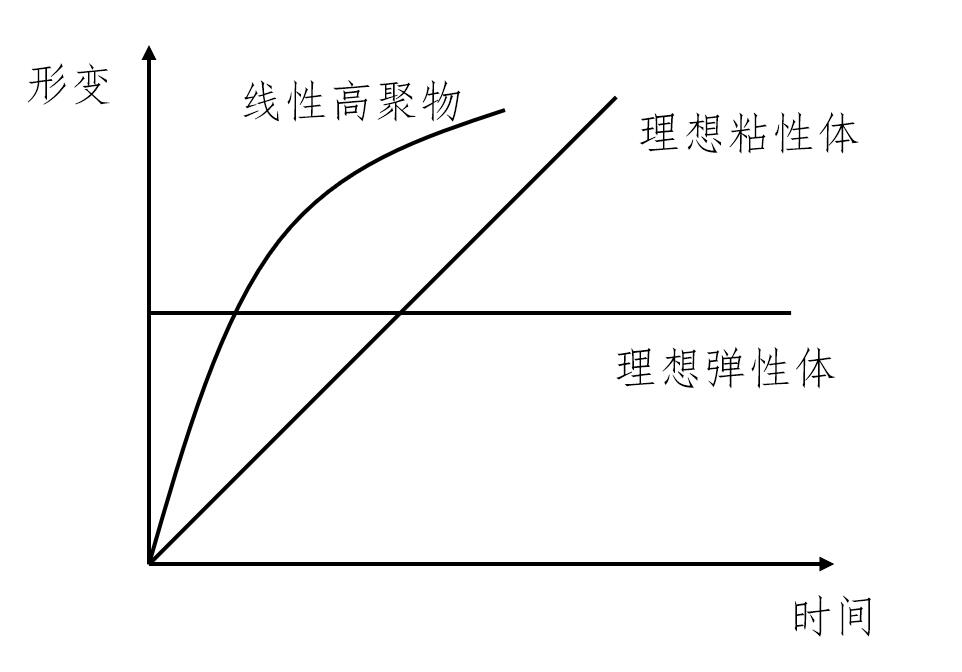
国内外许多学者在复合材料蠕变方面进行了许多理论研究，他们主要是基于粘弹性理论设计各种物理模型，再通过设计实验，验证模型对于不同条件下蠕变的适用性，其中经典模型有Maxwell模型和Kelvin模型。他们通过一个理想弹簧和理想黏壶的串并联组合，用来描述复合材料的蠕变或松弛过程。之后学者们建立的Burgers模型和多元件模型也都是基于这两个基本模型。这些模型是考虑到基本模型的设计过于简单，而采用多元件多重串并联组合设计而成的，它们在表征材料在不同工况下的蠕变性能时更加准确。

此外，通过对蠕变实验现象进行数学描述，学者们建立了参数法唯象蠕变模型，主要有Findley模型、Sun和Gates模型以及蠕变主曲线法^[7]。这些模型的建立摆脱了固定函数式的束缚，仅用一个数学模型。通过设计数学模型中的参数，可以考虑温度、湿度、荷载等多因素对复合材料蠕变的影响，考虑更加全面且使用简单方便。

近些年来，在研究复合材料高温条件下蠕变性能方面，学者们也做了大量的工作。陈素芳，谭志勇等人通过建立细观有限元模型，对复合材料力学性能和热膨胀性能进行了预测，并建立了预测方法^[9]；Yasushi Miyano, Masayuki Nakada等人通过三点弯曲实验测量CFRP复合材料在不同吸水量与不同温度下蠕变的实验数据，再利用时温等效原理绘制主曲线，进而预测层合板在任意温度和任意吸水量下的长期力学性能^[10]；W.K. Goertzen, M.R. Kessler利用玻璃化转变弛豫的活化能法和手动平移法计算时温等效的转换因子，建立了蠕变主曲线模型，并验证了活化能法在低于玻璃化转变温度Tg的适用性^[11]；Valentino Paolo Berardia, Michele Perrella等人对FRP层合板及其构成相（纤维和基体）分别进行拉伸实验研究，在长达4800h的实验中，测试其蠕变性能，并分别建立微观力学模型和现象性非线性模型来对不同构成相进行力学性能预测^[12]。T. Pulngern, T. Chitsamran等人在范围为20℃-70℃的梯度温度下对WPVC复合材料进行拉伸、压缩和弯曲实验，并分别建立时间-应力蠕变模型和时间-应力-温度蠕变模型以实现不同条件的力学性能预测^[13]。

在细观力学方面，学者们对于不同的纤维铺层、纤维长度、制作工艺等方面建立了许多混合律模型。张斌，顾伯勤等人基于复合材料的界面、纤维和基体三种组成成分建立了预测模型和预测公式，并通过实验验证模型的合理性 ^[14]；任超，陈建钧等人主要研究了随机短纤维复合材料的理论模型设计，建立了二维和三维模型以及相应的预测公式 ^[15]。江冰，吴代华采用细观力学的方法设计了正交铺层复合材料的理论模型，并推导出了复合材料力学参数的计算公式，通过实验检验，模型设计合理 ^[16]。

在高温蠕变方面，目前大多数研究都集中在复合材料在拉伸、压缩和剪切荷载下的蠕变行为，关于弯曲荷载下蠕变行为研究较少。而受弯应力状态又是复合材料结构产品中的普遍力学现象，因此需要为工程中受弯曲荷载的复合材料提供可靠的蠕变性能数据^[17]。在细观力学方面，学者们对不同种类复合材料建立模型繁多，但关于混合律对复合材料高温蠕变的适用性研究较少。

本文进行了GFRP复合材料在弯曲荷载下高温加速蠕变实验，做到了荷载方面的创新。利用高温蠕变数据，建立了GFRP复合材料的蠕变主曲线模型研究其长期性能变化，并创新地推导出包含时间和温度双变量的蠕变数学函数。之后，验证了混合律对于高温蠕变的适用条件，这也是本文的创新之处。

1.3 研究内容

本文主要内容分为五个方面：（1）开展复合材料高温蠕变实验；（2）长期蠕变主曲线模型；（3）短期蠕变Burgers模型；（4）蠕变混合律模型；（5）必要分项系数的对比

（1）高温蠕变实验

本文针对玻璃纤维增强不饱和聚酯树脂复合材料，开展了两部分实验：（1）高温环境下树脂浇铸体的模量与强度保留率的实验；（2）玻璃纤维增强塑料的高温弯曲蠕变试验。实验一采用三点弯曲的实验方法和位移控制模式，通过加载至材料破坏失效，测量树脂浇铸体的弹性模量和弯曲强度。实验二选用树脂浇铸体试样（基体R）、玻璃纤维短切毡手糊试样（CSM）和连续玻璃纤维缠绕环向试样（WR）三种试样，并采用三点弯曲的实验方法在低应力作用下进行不同温度的弯曲蠕变实验。

（2）长期蠕变主曲线模型

基于时温等效原理，利用高温蠕变实验结果，建立两种复合材料的蠕变主曲线模型，并对主曲线进行拟合和对比分析。采用了活化能法确定主曲线的移动因子，其中利用Arrhenius公式求解移动因子^[11]。

（3）短期蠕变Burgers模型

针对各温度下的短期蠕变实验结果，采用Burgers模型对实验曲线进行拟合，得到各项蠕变性能参数随温度的变化规律 ^[18]。

（4）蠕变混合律模型

针对两种铺层的GFRP复合材料，采用不同的混合律模型，得到混合律计算公式，再结合复合材料及树脂浇铸体蠕变实验结果对模型进行检验。

（5）必要分项系数的对比

利用树脂浇铸体的弯曲模量与强度保留率实验和高温蠕变实验数据，从不同方面确定树脂浇铸体考虑高温蠕变的必要分项系数，并与GB51160中分项系数进行对比 ^[19]。

第2章 GFRP复合材料高温蠕变实验

2.1 实验原理

复合材料的蠕变实验同其他材料实验一样，有拉伸、压缩和弯曲等加载方式。而采用弯曲试验的原因有以下几点：（1）复合材料的蠕变主要由树脂的蠕变所决定，采用弯曲试验相比之下更能反映树脂基体的蠕变情况；（2）受弯应力状态是工程构件的普遍受力状态，弯曲试验综合体现了材料的拉、压、剪等力学性能，能够更好地反映复合材料特性。综合以上几点，采用弯曲试验来研究复合材料高温蠕变更为合适^[17]。

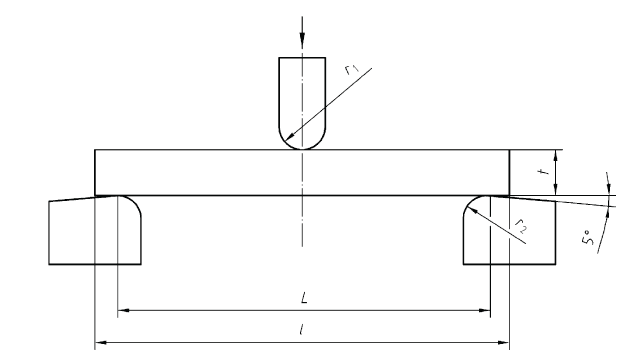
三点弯曲实验是将试样放置在两支点上，通过中间的加载压头施加集中荷载，同时通过仪器中的传感器读取荷载大小以及中点的位移，计算机每隔一定时间读取数据，并输出到原始数据文件中。实验中的测量数据为试样中点的弯曲挠度。对于普遍的纤维增强材料，E/G=5~10，剪切变形挠度所占比例不大。基于小变形假设和材料力学中挠度计算公式，可得材料的蠕变柔量计算公式如下：

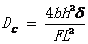（2.1）

其中为试样中点弯曲挠度，b为试样宽度，h为试样厚度，L为加载装置两支点间距离，F为施加荷载。

通过蠕变柔量可进一步计算蠕变模量和模量保留率等力学参数，进而分析复合材料的高温蠕变性能。

2.2 试样制备

2.2.1 试样选材

本实验采用的树脂为常用结构树脂：间苯型不饱和聚酯树脂FC518，由上海富晨化工有限公司提供。增强材料选用无碱纤维增强材料，增强材料规格分别为缠绕纱2400Tex、短切毡450 g/，是由河北中意复合材料有限公司提供。

实验试样分为三种：树脂浇铸体（基体R）、玻璃纤维短切毡手糊试样（CSM）和连续玻璃纤维缠绕环向试样10层（WR）。其中WR试样采用的铺层工艺为纯环向缠绕，CSM试样为采用手糊制作工艺制作板材。所用的试验材料的配料比及相关参数可见下表2.1

2.2.2 试样参数

本实验通过实验标准制定试样尺寸，试样理论厚度h=5mm，宽度b=，长度，加载装置跨距为64mm。每个试样设置5个温度梯度，每个温度下对应2个试样。试样要求尽量厚度均匀，但试样采用手糊工艺制备，会导致厚度不均匀。试样中玻璃纤维密度为2580，树脂密度为1150，树脂基体的热变形温度为80℃。试样的配料比如下表：

表2.1 实验材料试样配料比

2.3 实验设备

实验采用INSTRON5848万能材料试验机（如图2.1）施加荷载，使用匹配环境箱（如图2.2）提供恒温环境，并通过计算机自动读取试验数据，时间间隔为0.1s。基本试验装置如图2.3，图2.4所示。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：