摘 要

原子力显微术（AFM）是一种纳米级表面探测技术，在纳米科学领域发展过程中发挥着非常重要的作用。AFM也分为不同的工作模式，其中，振幅调制AFM（AM-AFM）是一种比较主流的AFM，它不仅可以获得样品表面的形貌图像，还可以探测样品的表面材料性能信息，所以近年来获得了快速的发展。本文介绍了AM-AFM基本测试原理，描述了探针动力学特性的几个常用力学模型，并且给出了相应的力学模型的适用范围。利用数值计算方法得到了非线性动力学系统的响应，并从时域和频域两个不同方面对探针非线性动力学响应进行了分析。研究了样品不同力学性能对探针非线性动力学响应的影响，建立了样品力学性能变化与探针非线性动力学响应变化之间的关系，并能用于指导相关实验工作的开展。

关键字：振幅调制原子力显微术；数值计算；时域；频域；探针

Abstract

Atomic force microscopy (AFM) is a nanoscale surface detection technology, which plays a very important role in the development of nanoscale science. AFM is also divided into different working modes. Among them, amplitude modulation AFM (AM-AFM) is a relatively mainstream AFM, which can not only obtain the morphology image of the sample surface, but also detect the surface material performance information of the sample, so it has achieved rapid development in recent years. In this paper, the basic testing principle of amplitude modulation atomic force microscopy (AM-AFM) is introduced, several commonly used mechanical models of probe dynamics are described, and the applicable scope of corresponding mechanical models is given. The response of the nonlinear dynamic system is analyzed by numerical method, and the nonlinear response of the probe is analyzed from two different aspects: temporal response and spectral response. The effects of different mechanical properties of samples on the nonlinear dynamic response of probes were studied, and the relationship between the changes of the mechanical properties of samples and the changes of the nonlinear dynamic response of probes was established.

Keyword：Amplitude modulation atomic force microscopy（AM-AFM）；Numerical calculation；temporal response；spectral response；tip

目 录

第1章 绪 论 1

1.1 目的及意义 1

1.2 研究的基本内容 2

1.3 振幅调制原子力显微术的基本原理 2

1.4 振幅调制原子力显微镜的基本组成 2

第2章 振幅原子力显微术理论基础 3

2.1 针尖-表面间相互作用力模型 3

2.1.1 范德华力 3

2.1.2 Derjaguin-Muller-Toporov模型 4

2.1.3 非保守力 4

2.1.4 粘弹性材料 5

2.2 微悬臂探针系统 6

2.2.1 运动方程 6

2.2.2 点质量模型 6

2.2.3 连续微悬臂模型 7

2.2.4 点质量模型和连续微悬臂梁模型的等价性 8

第3章 振幅原子力显微术动力学分析 10

3.1 程序设计 10

3.2 平均针尖-表面间距的影响 12

3.2.1 参数设置 12

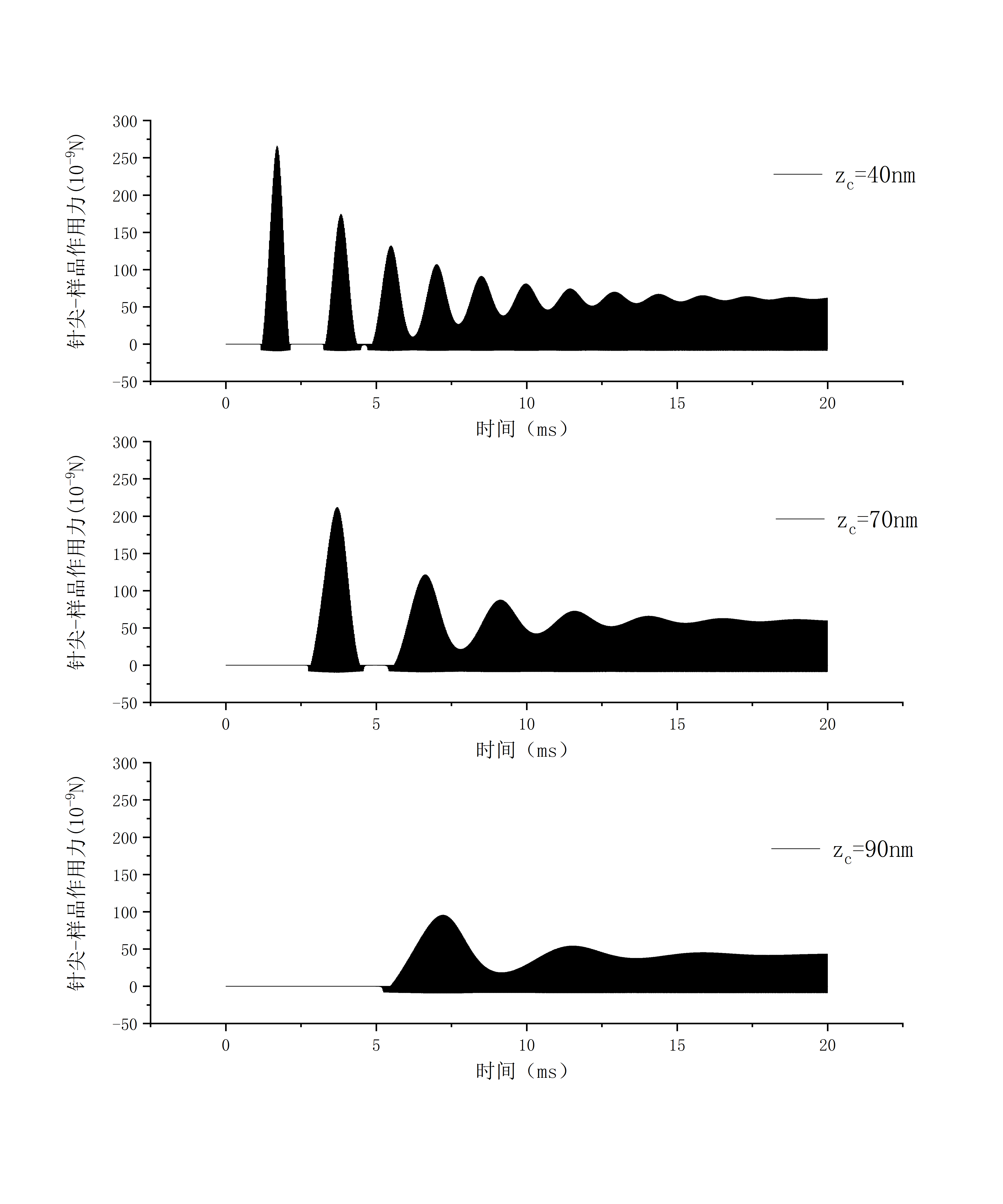
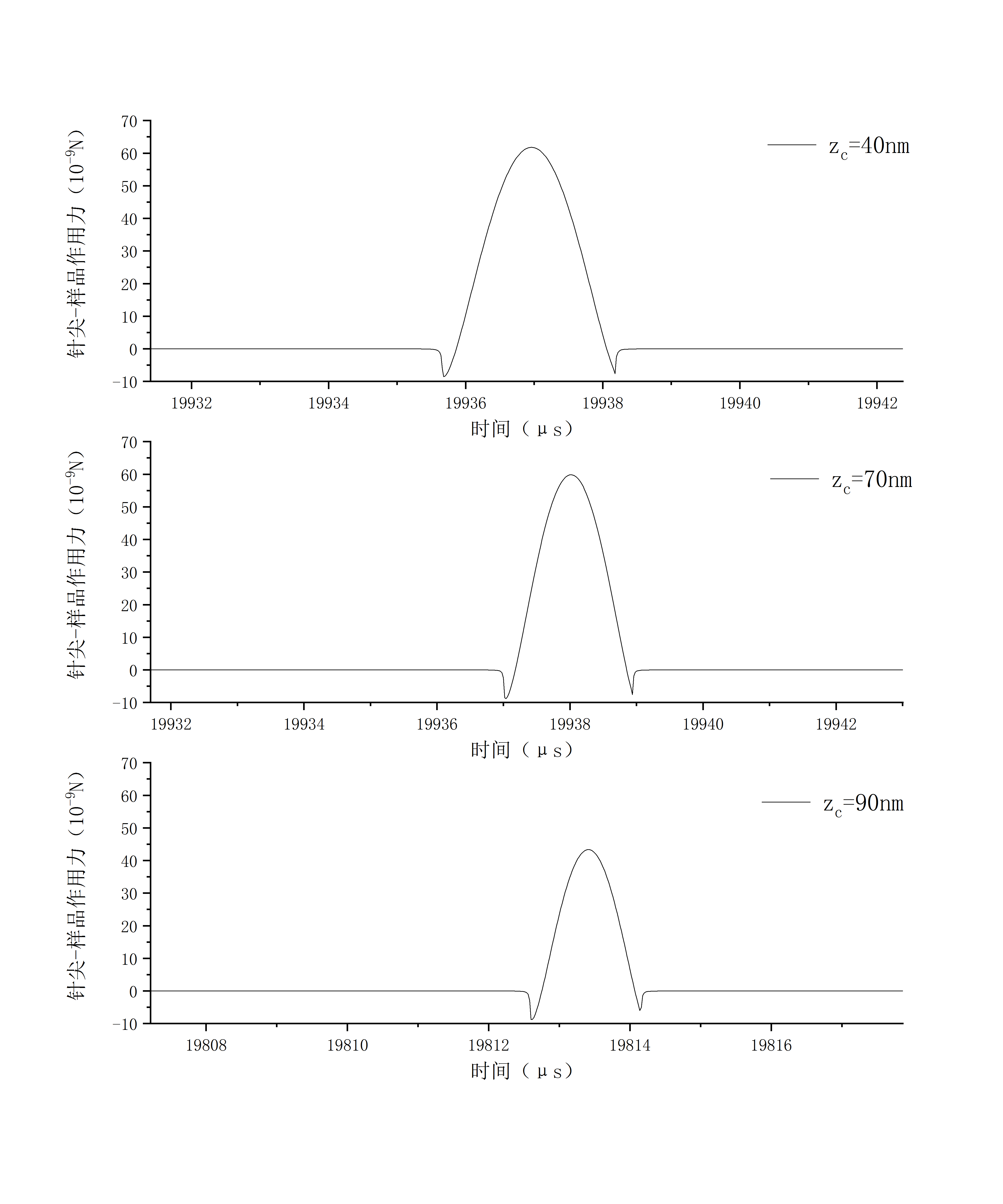
3.2.2 时域分析 13

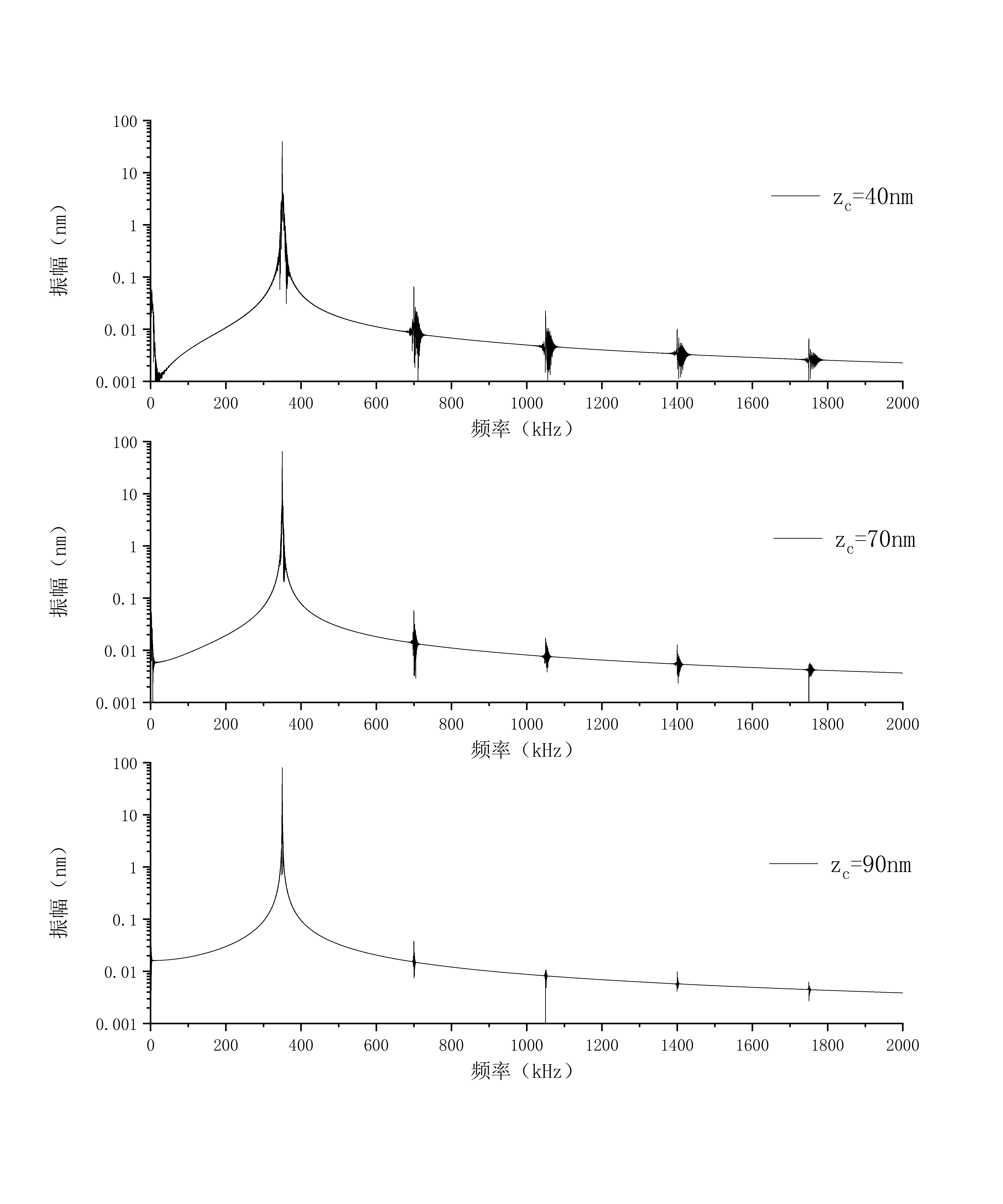
3.2.3 频域分析 17

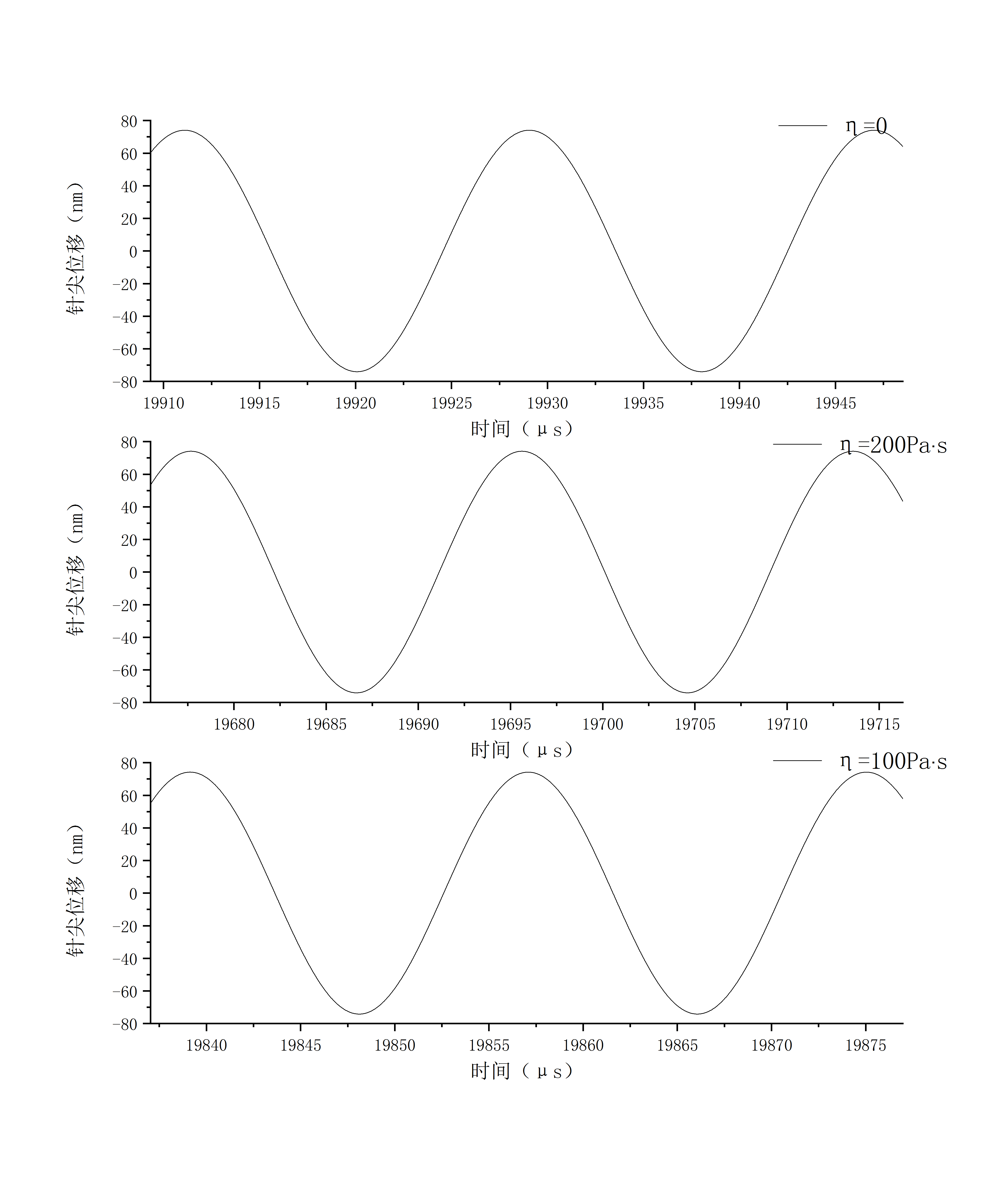
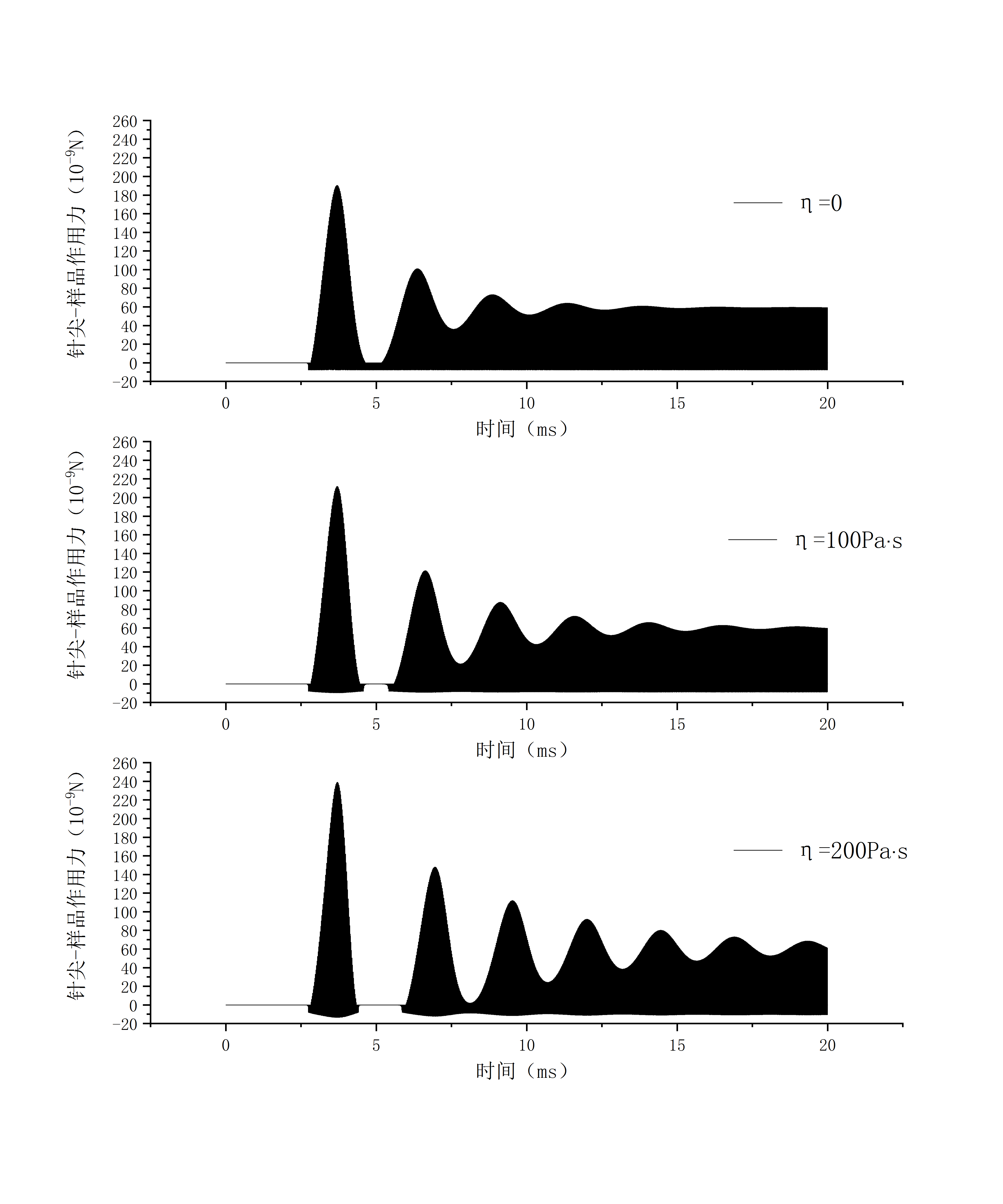
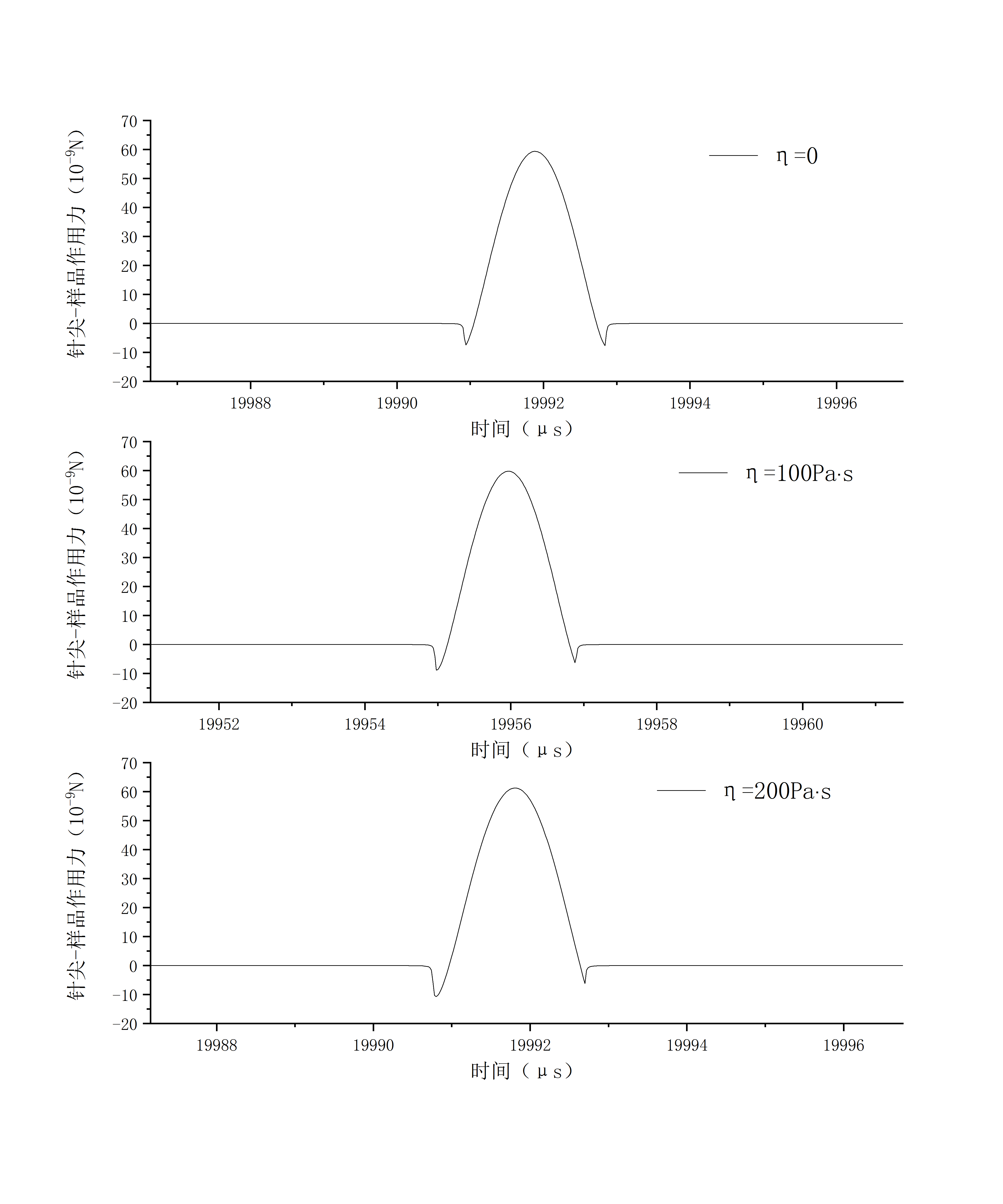
3.3 黏度系数的影响 18

3.3.1 参数设置 18

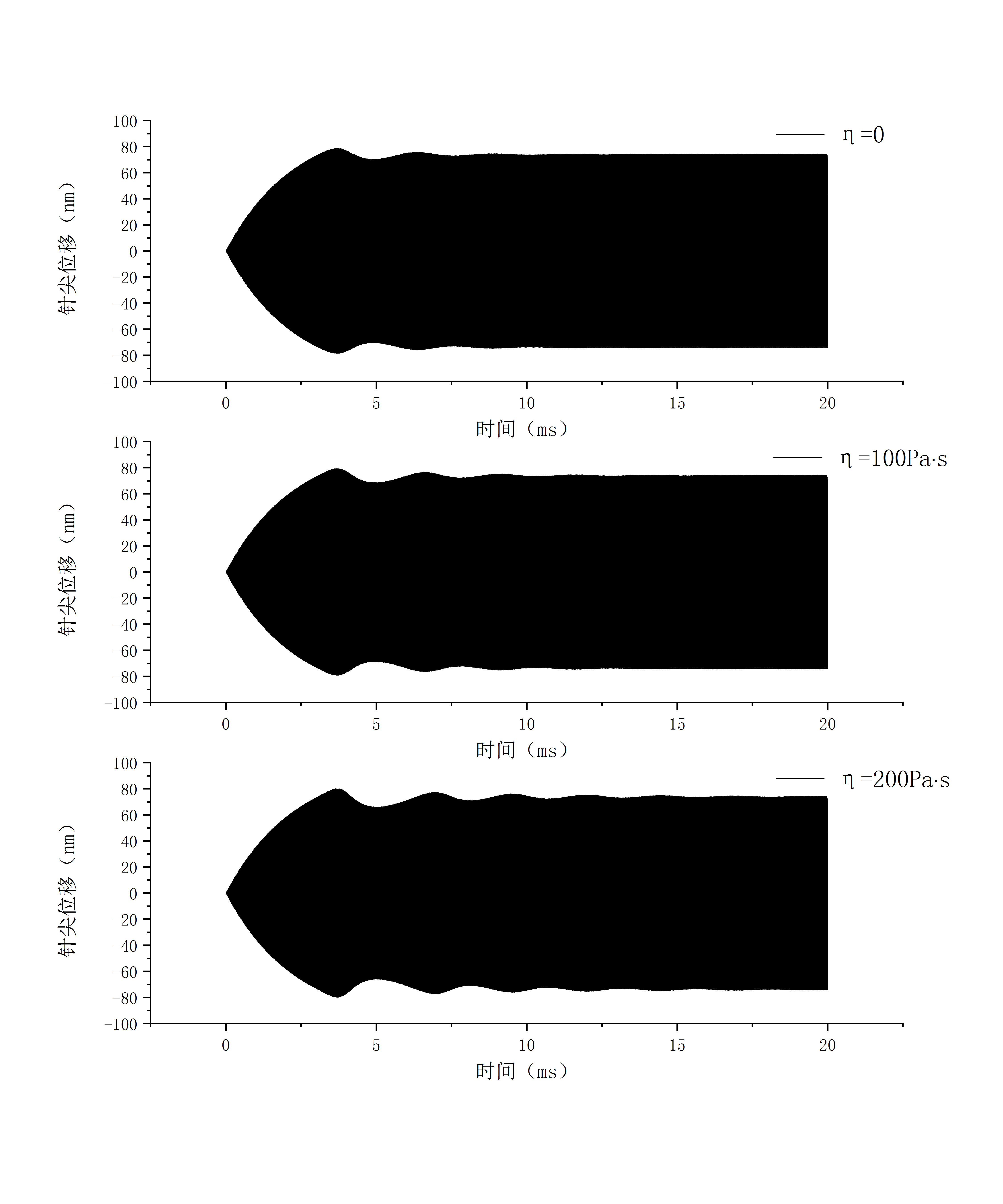
3.3.2 时域分析 19

3.3.3 频域分析 23

3.4 样品弹性模量的影响 25

3.4.1 参数设置 25

3.4.2 时域分析 26

3.4.3 频域分析 30

第4章 结 论 31

参考文献 32

附录A 33

致 谢 38

绪 论

目的及意义

原子力显微术(Atomic Force Microscopy，AFM)发展于20世纪80年代，是一种样品表面探测技术，针尖-样品相互作用力的大小和性质会随着针尖与样品间距离的变化而变化，因此能够获取样品表面的多种信息，最后达到检测目标。AFM的优点有以下四点：

• 检测对象非常广泛
• 不会受到导电性能的制约
• 适用性很强(液体、真空、大气的条件下皆可操作)
• 能够实现很高的分辨能力

AFM作为纳米级表面探测技术，在纳米科学领域发展过程中发挥着非常重要的作用。在纳米技术领域，纳米材料的研究要求已经由单纯探测样品表面形貌特征，拓展到能够获取表面材料性能信息，这在某种程度上也快速促进了AFM的发展。近几年，获得材料表面形貌并估计其表面材料力学性质，已经成为原子力显微技术相关领域研究的热点问题和发展的重要方向，原子力显微术在技术和原理上的变革已经悄然发生。

最初，原子力显微术仅仅用来探测微悬臂静态偏转的静态模式，然而这几年已经发展到可以探测微悬臂梁探针振动的动态模式。为了获取样品形貌，静态模式AFM常利用微悬臂探针随着样品表面起伏而产生静态偏转。可是，在检测样品的过程中，静态模式下的微悬臂梁探针很可能与样品之间产生横向摩擦力，使样品或针尖产生破坏，从而使图像的效果大大降低。与之相比较而言，动态模式AFM优势明显，有以下四点优点：(1) 针尖-样品间的横向摩擦力被降到最低；(2) 振幅调制模式下的幅度、频率和相位等多种参数均可用来表征样品表面性能；(3) 可用于细胞、蛋白质和DNA等样品的成像，因为其针尖-样品的相互作用力极其微弱，约为1 ×10^-9N；(4) 谐波成像模式来自于振幅调制模式，可以在成像同时获得样品表面形貌以及物理性能参数。

看到动态模式AFM的以上优点，我们就希望对动态模式AFM的动态响应进行理论分析和数值模拟，为今后提高实验样品成像分辨率和实现材料性质的表征提供理论依据。振幅调制模式AFM（亦称为AM-AFM）是一种比较主流的动态模式AFM，本课题就是对AM-AFM的悬臂梁模型进行动力学时域和频域的分析，其中涉及到振动力学的基础知识，是了解AM-AFM工作原理的前提。

研究的基本内容

AM-AFM是一种新型的纳米尺度表面探测技术，其不仅能够获得样品表面的形貌，而且能够得到样品表面的多种物理性能信息。微悬臂探针系统动力学分析力学模型分为点质量模型和连续微悬臂梁模型，此处点质量模型常用于自激励模式，而连续微悬臂梁模型一般用于多模态动力学分析。常用的针尖-表面相互作用力模型有Derjaguin-Muller-Toporov (DMT)模型，适用于描述弱黏附力和小针尖半径下硬接触的情况。由于难以获得解析解，可以利用有限差分法等数值计算方法，分析非线性动力学系统的响应，并获得时域和频域两个不同方面的响应图像。最后，研究样品不同力学性能对探针非线性动力学响应的影响，初步建立样品力学性能与探针非线性动力学响应之间的变化关系，最后将结论用于指导实验相关工作。

振幅调制原子力显微术的基本原理

微悬臂梁末端有一个类似针尖形状的探针，是AM-AFM的基本结构，其随着微悬臂梁在样品的表面上方上下振动。微悬臂梁的弯曲共振频率容易获得，微悬臂梁受到这个固定频率的激励。针尖振荡的振幅相对自由状态会减小，这是因为微悬臂梁受到针尖-表面相互作用力的作用。为了实现样品表面形貌的成像，需要获得振荡振幅以及外部激励与针尖运动的相位差，然后得到振幅的反馈参数。针尖-样品相互作用力的正值为排斥力，负值为吸引力。对于那些化学成分固定的针尖-表面组合，自由振幅、针尖尖端半径、用于反馈的设定振幅大小以及成像工作区域，都决定了针尖与样品之间的相互作用力的大小和正负。

振幅调制原子力显微镜的基本组成

通常情况下，探测单元、微悬臂梁探针系统、针尖-样品运动单元、反馈控制器以及图像处理系统这五个部分组成了原子力显微镜。此处探测单元、微悬臂梁探针系统、针尖-样品运动单元可以集成为一体，我们称之为AFM主机。

振幅原子力显微术理论基础

针尖-表面间相互作用力模型

范德华力

电磁场涨落是产生长程范德华力的主要原因，同时热涨落和量子零点涨落也对长程范德华力有影响。目前，为了描述范德华力，国内外已出现了许多复杂的理论模型，下面介绍几种常见的模型。

电偶极矩相互作用导致了原子或分子间的范德华力，既可以是是固有的电偶极矩，也可以是其他固有电偶极矩或热涨落。诱导偶极-诱导偶极、偶极-诱导偶极和偶极-偶极，是三种可能的以1/r⁶形式衰减的偶极相互作用势，其中r为分子或原子间的间距。通常，原子力显微成像实验面对的是分子或原子体系，样品与针尖表面原子间所有的偶极作用相互叠加，最后称为总的范德华力。锥球体-平面和平面-球体几何结构是描述AFM界面最常见的两种近似结构。平面-球体的结构中，范德华力由下式给出：

(2.1)

此时，d称作瞬时表面-针尖间距；R称作针尖半径；H称作Hamaker常数。当d→0时，式(2.1)是发散的。为规避上述的发散情形，所以在间距d小于分子的间距a₀的时候，从接触力学模型推算得到的黏附力在某种程度上等同于范德华力。分子间距a₀参考标准为0.165nm。材料和介于中间的介质能够决定Hamaker常数，典型值的大小在10^-20J量级。

半球针尖的锥形探针的范德华力如下：

(2.2)

此时，β为圆锥半角，且R_β=R(1-sinβ)。在dlt;R时，半球形盖对范德华力起决定性作用，式（2.2）也可简化近似为式（2.1）。

一系列半球可以用来近似描述粗糙的样品表面，范德华力利用球-球近似得到：

(2.3)

此时，R_t是针尖半径；R_s是与针尖位置对应的样品区域的等价有效半径。

一般情况下，两个表面间的范德华力是吸引力。任意介质中两种相同材料间的范德华力总是吸引力。总的来说有三种不同的情况。真空或大气环境下，不同材料间的范德华力是吸引力。液体的环境下，不同材料间的范德华力可能是吸引力也可能是排斥力，这取决于介电常数的大小和界面的折射率。

Derjaguin-Muller-Toporov模型

Derjaguin-Muller-Toporov(DMT)模型可以用来描述小针尖半径和弱黏附力的硬接触。DMT模型假设黏附力存在于接触区域外围，表示为：

（2.4）

接触时还存在来自于分子、原子层次的泡利和离子排斥力：

， （2.5）

此时，γ是表面能（W_ad=2γ）。下式表示为接触面积：

（2.6）

此时，F是施加的作用力。

可以看出，当针尖样品接触时，z z_c的负值表示压入样品的深度δ，而正值代表着瞬时针尖-表面间距d。DMT模型下的压入深度与施加力的近似关系表达式如下：

（2.7）

非保守力

在许多实验中，也会经常遇到非保守力。这取决于环境和材料，许多不同的物理过程都可能导致能量耗散。例如，针尖-样品的相互作用力所导致的分子或原子的交错、重新取向，样品和针尖之间的分子或原子交换，或者半月形毛细液滴的形成和破裂。

速度依赖过程和表面黏附回滞是纳米尺度的能量耗散的两个主要机制。表面黏附回滞的产生主要有两个原因：一个是来自于短程原子和分子间的相互作用，另一个是来自于长程的相互作用。其主要概念是，存在表面黏附回滞的时候，两个表面接触时获得的能量总是小于将两个表面分离所需做的功。所以，系统表面能会有两个值，一个是离开半周期的γ_r，另一个是靠近半周期的γ_a。比如，DMT模型的理论下，其表面黏附回滞的大小为：

(2.8)

此时，γ_a和γ_r分别用于微悬臂探针靠近和离开样品表面时的半周期。

通过计算时间依赖的幂次相互作用，可得到不包括样品与探针物理接触的非基础耗散作用力，亦称为长程耗散界面力：

(2.9)

此时，探针是远离(α_r )还靠近(α_s )表面决定了力强度α。

结合Hertz接触模型获得的样品形变与Voigt模型给出的应力和应变关系，我们能够列出黏滞力简化后的表达式。时间依赖黏滞力的大小为：

(2.10)

此时，η为黏度。同时，值得注意的是，形变大小和形变速率都决定了黏滞力的大小。

粘弹性材料

现有一个由粘弹性材料构成且不存在表面黏附回滞的界面，表面与针尖相互作用力包括接触排斥和长程范德华力。表面与针尖接触之前，针尖-表面间相互作用力主要就是范德华力：

(2.11)

表面与针尖接触之后，就必须考虑黏滞力、接触排斥力以及黏附力。此时，黏滞力由（2.8）给出，这里的前两项由DMT模型给出：

(2.12)

d=a₀的时候我们可认为黏滞力与范德华力在某种意义上相等：

(2.13)

微悬臂探针系统

运动方程

建立微悬臂探针系统的动力学方程是振幅调制原子力显微术的理论基础。一般情况下，人们把微悬臂探针看作矩形悬臂梁，这种近似方案可以大大简化问题的求解。矩形悬臂梁具有对称的特点，所以微悬臂探针的运动可利用偏微分方程表示。引入针尖-表面相互作用力和一些耗散项后，我们可以得到一个修正后的欧拉-伯努利方程：

(2.14)

此时，d=z₀ z_c w(x,t)是瞬时的针尖-表面间距离；w(x, t)是垂直于其主轴方向的微悬臂梁的位移；I、E和ρ分别是面积惯性矩，杨氏模量和质量密度；h、L和W分别是厚度、微悬臂梁的长度和宽度；a₁、a₀分别是内部和外部耗散系数；F_exc(x,t)是微悬臂梁所受到的激励力；F_ts(d)表示针尖与表面间相互作用力的总和。δ(x-L)函数的含义是针尖与表面的相互作用力仅作用于微悬臂梁末端针尖位置。系统在介质（空气、液体或真空）中运动的影响被近似忽略不计。以上的动力学运动方程中，微悬臂梁的质量远远大于针尖质量，所以针尖质量可以忽略不计。但是，针尖-表面间相互作用力实际上受到了针尖几何形状的影响。

为了求得上式（2.14），确定针尖-表面的相互作用力的数学表达式和边界条件是前提，方程允许的解的数目取决于边界条件。连续系统的铅垂z方向上的多个运动模式需要在数学处理过程中加以考虑。上述模式一般被叫做共振模式。在不考虑内部耗散的情形下，微悬臂拥有无数个共振模式。为了得到式（2.14）的解析表达式或半解析表达式，多种数学技巧与工具都将会被使用到。为了求解上述方程，目前多种代替性的理论和计算方法已被提出。

点质量模型

描述AM-AFM系统最直接的模型就是点质量模型。微悬臂梁探针系统被近似看作一个处于针尖-表面相互作用力和外界激励力下的点质量弹簧，利用振动力学知识可获得一个二阶偏微分方程，表示如下：

(2.15)

此时，F₀和ω分别是激励力和角频率；ω₀、Q、m^*、和k分别是自由微悬臂的自然角频率、品质因数、有效质量和力常数。此时m^*=0.25m_c。在振幅调制模式原子力显微（AM-AFM）中，激励频率接近于微悬臂梁的一阶共振频率。

连续微悬臂模型

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：