湍流中POD和DMD两种特征提取方法的初步对比研究毕业论文
2020-02-18 10:05:24
摘 要
描述流体流动的拟序结构对理解流体动力学和输运过程是至关重要的。本文介绍了两种从直接数值模拟或物理实验中获得的流场数据中提取拟序结构的方法,即正交模态分解(Proper orthogonal decomposition ,POD)和动态模态分解(Dynamic mode decomposition ,DMD)。正交模态分解提取的模态按照能量大小排序,且每一阶模态基本都是多频率耦合的。而动态模态分解方法按照不同的频率进行模态提取,并且此方法可以进行流场稳定性分析。最后利用了展向旋转槽道湍流的数据,应用这两种模态提取方法,提取流场中的拟序结构。发现两种方法都可以提取出流场中的涡胞结构,但是POD方法提取的模态更加清晰。
关键词:正交模态分解;动态模态分解;展向旋转槽道湍流
Abstract
The description of coherent structure of fluid flow is crucial to the understanding of the fluid dynamics and transport processes. This paper introduces two methods to extract the coherent structure of the flow field data obtained from numerical simulation or experiments. They are Proper orthogonal decomposition (POD) and Dynamic mode decomposition (DMD). The modes extracted by POD are sorted by energy, and each mode generally contains a mixture frequencies, while the DMD method extracts the modes by different frequencies. Besides, the DMD method can also analyze the stability of flow field. Finally, we extract the modes by these two method, based on the data of numerical simulation of turbulent channel flow with spanwise rotation. We find that both methods can extract the large-scale roll cells in the flow field, and the POD method can extract the mode more clearly.
Key Words:POD;DMD;turbulent channel flow with spanwise rotation
目 录
第1章 绪论 1
1.1前言 1
1.2 研究意义及内容 2
第2章 模态分解方法原理 3
2.1 POD方法原理 3
2.1.1 速度场是连续函数的情况 3
2.1.2 速度场是离散函数的情况 6
2.2 DMD方法原理 9
2.2.1 DMD原理推导 9
2.2.2 求解DMD方法的振幅矩阵 12
2.2.3 损失函数、模态频率和模态增长率的定义 13
第3章 展向旋转槽道湍流计算模型 16
第4章 模态分解方法提取结果 18
4.1 POD方法提取结果 18
4.2 DMD方法提取结果 23
4.3 两种模态分解方法对比 29
4.4 两种模态分解方法优缺点总结 30
第5章 结论 31
参考文献 32
附录A 35
附录B 36
附录C 38
致谢 42
第1章 绪论
1.1前言
一直以来,湍流都被认为是经典物理留下的世纪难题[1]。著名的雷诺实验,发现了管道中流体的流动可以呈现两种截然不同的流态,即层流和湍流。但是直到现在,学界也无法对湍流下一个准确的定义。一般将具有无规则性、扩散性、连续性、粘性耗散以及流动雷诺数较大的、有三维尺度上的脉动涡旋的流动状态称为湍流。现实生活中遇到的湍流问题基本满足了以上特性,如燃烧室中气体的流动、江河中的急速流动、船舶和飞行器表面的绕流等等。
流体的运动学和动力学行为服从质量、动量和能量三大守恒定律,并由这三大守恒定律定量确定。经典流体动力学的主要成就就是建立了描述流体运动的控制方程,如经典的Euler方程和Navier-Stokes方程。湍流显然也是由这些控制方程所定量描述的。遗憾的是,这些控制方程绝大多数无解析解,只能采用各种数学手段求其近似解。流动的数值计算研究一般有三种方法:直接数值模拟(Direct numerical simulation ,DNS),雷诺平均N-S方程(Reynolds Average Navier-Stokes ,RANS)和大涡模拟(Large-eddy simulation ,LES)等等。但是DNS需要巨大的计算机运算量,RANS和LES方法的计算精度不及DNS。而实验测量中,测量设备对流场的扰动也会产生相应的误差。所以湍流的研究还有着重重困难。但是不管是实验还是数值模拟,都会产生大量的数据。这些数据的后处理也决定了能不能从算例中获得有价值的信息。
现今,很多学者已经把模态分解作为以上数据后处理的工具。通常,模态分解取一组流场数据并从中计算出一组模态或特征。而这些模态的意义取决于所使用分解的特定类型。Lumley在1967年首次将正交模态分解(Proper orthogonal decomposition ,POD)方法引入湍流研究。而后Sirovich 在1987年引入了Snapshots方法,这是经典POD方法的一种变体,使计算更加简便[2]。总而言之,这两种POD方法都是将流场数据分解为三个矩阵,即空间相关矩阵、时间相关矩阵和与流场能量相关的一个对角矩阵。空间相关矩阵包含了POD模态,即流场中比较重要的空间结构。POD方法除了进行模态分解,还可以与Galerkin投影方法相结合,对由偏微分方程组成的流体力学方程进行降维处理[3]。该方法在不同领域有不同的名称:POD、主成分分析法(principal component analysis ,PCA)、Hotelling分析、经验成分分析(empirical component analysis)、经验特征函数分解(empirical eigenfunction decomposition)等等[4]。还有一种比较常用的方法是Schmid在2010年提出的动态模态分解(Dynamic mode decomposition ,DMD)[5]。该方法同样将流场数据分为了三个矩阵,不同于POD方法按照能量进行排列,DMD方法按照频率进行模态的排列。DMD方法一个很重要的优势是,它能对提取的模态进行稳定性分析。由于DMD方法深深扎根于线性代数,因此该方法具有很高的可扩展性,从而促进了算法的发展[4]。
通过阅读文献,发现模态分解技术已经有了很广泛的应用。如跨声速抖振模态分析[6]、圆柱绕流稳定性的分析[7]、壁湍流问题[8]、对称槽道涡波流场流动特征分析[9]以及湍流大尺度信息提取与分析[10]等等。DMD方法在横向射流、带襟翼机翼尾流和动失速尾流等复杂流动现象上也有广泛应用[6]。研究某一个问题时,一般不是单独使用POD方法或者DMD方法,而是将POD方法和DMD方法提取的结果进行对比,观察哪种方法提取结果的物理含义更加明确。
这两种方法也有各自的缺点。比如对于POD方法,能量不一定在所有情况下都是对流动结构进行排序的正确方法[5]。再如DMD方法,由于DMD方法提取的模态中描述的结构只与离散频率有关,因此不太可能描述多频的拟序结构。
最近也有学者提出了光谱自正交分解(Spectral Proper Orthogonal decomposition ,SPOD)[11-12]、稀疏促进动态模态分解(Sparsity-promoting dynamic mode decomposition)[13]等方法来解决上述POD方法和DMD方法的缺点。
1.2 研究意义及内容
POD方法和DMD方法及这两种方法的变体,已经被广泛应用于湍流场数据的后处理。通过这两种方法,可以有效地提取出流场中主要的拟序结构,为流场的动力学分析和输运过程提供了有效的信息。但是对于展向旋转槽道湍流的提取研究还比较少,因此本文对此问题进行了分析和处理。
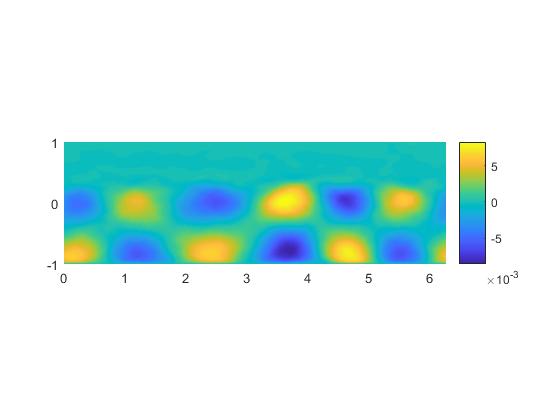
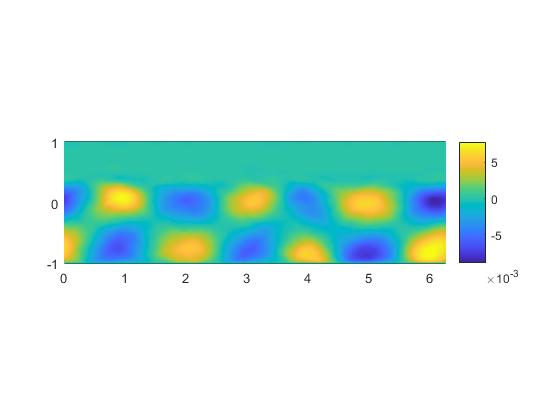
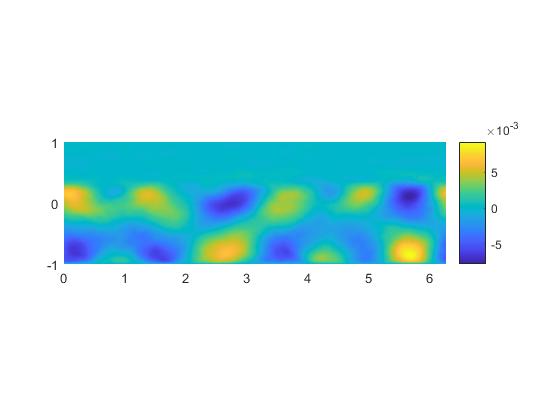
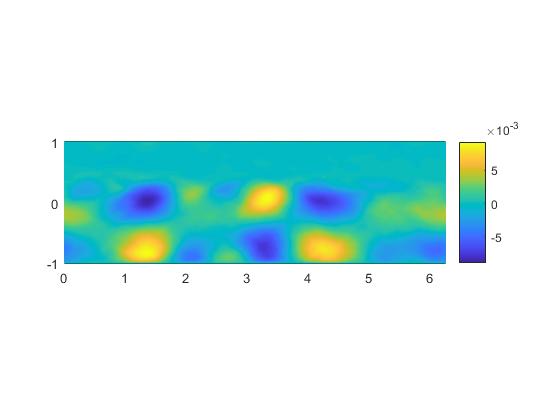
本文将主要叙述POD和DMD这两种方法,并编写Matlab程序对展向旋转槽道湍流数据进行模态提取,希望能提取出流场中的涡胞结构。这些涡胞结构对湍流结构和平均剖面有很大影响。Matlab代码的编写参考了文献[14],具体的代码详见附录C。
第2章 模态分解方法原理
本章,将分别介绍两种模态分解方法的原理。这两种方法都是对流场数据进行处理,进而提取流场中的拟序结构。POD方法的推导主要参考了蔡庆东老师整理的文档,DMD方法的推导主要参考了文献[13]。其中附录A叙述了如何将原始流场数据转换为实际计算所使用的数据矩阵。
2.1 POD方法原理
2.1.1 速度场是连续函数的情况
速度场由空间坐标和时间坐标表示,它可以被分解为不随时间变化的稳态流场和脉动场,并且可以把脉动场用分量的形式书写:
(2.1)
(2.2)
这里的是空间位置变量,表示时间变量。记为矢量的维数,为空间的维数。
假设矢量函数可以用一组基函数来表示。由于是矢量函数,因此每个也是矢量函数,维数也为。那么对于每个j,如果,就有如下的表示形式:
(2.3)
有了上述表示的基函数,矢量函数可以展开为如下形式:
(2.4)
其中的是为了使得函数和具有归一性质,而引入的和空间坐标以及时间坐标都无关的常数。
显然,这种方法既适合矢量函数,也适合标量函数。如果矢量函数只有一个分量,上式也就转化为适用标量函数的形式。需要说明,将矢量函数每个分量当做一个标量函数的展开与对矢量函数的展开是不同的。
观察式(2.4)的形式,可以发现,如果有了基函数,那么,不论空间多复杂,都可以用M个时间函数的形式来表述未知问题。
为了使式(2.4)更有含义,要求式(2.4)的展开形式在所有M项的展开中,具有最优性质,即在给定的时空区域内的总体误差不超过任意同项数的其他展开。显然,为了满足以上条件,基函数的选择是和被近似的函数有关的。确定函数和的值,本质上是求如下泛函的极小值:
(2.5)
其中的平方运算更一般的表达方式是表示为两个矢量函数的内积,这个内积决定了误差范数的定义方式。
函数和都是未知函数,要求解这两个函数,要求泛函对未知函数的变分为零。首先,根据泛函对的变分为零,可得:
(2.6)
再根据泛函对的变分为零,可得:
(2.7)
其中是任意关于t的函数,是任意关于的矢量函数,并且可以将的项在展开式中去掉,这样做只是相当于减小了M,对结果是没有影响的。于是式(2.6)和(2.7)给出了确定未知函数和的方程组,也就是原泛函极小值问题的方程组,这是一组积分方程。流场中一般遇到的都是三维问题,也就是说。那么每个矢量函数包含三个未知函数,即,则总共有4M个未知函数。而方程数目也恰好为4M个,因此可以完全确定未知函数。将式(2.6)和(2.7)的方程组整理之后,可得:
(2.8)
除此之外,还要求函数和具有正交性,并且范数是单位值,即:
(2.9)
利用式(2.9)的正交性条件,式(2.8)化简为:
(2.10)
接下来,将方程组(2.10)的第一式两端乘,再将第二式代入,得到:
(2.11)
方括号内的部分记为积分核函数,用分量的形式表示为:
(2.12)
称此积分核函数为矢量场的时间相关函数,显然有
(2.13)
同样地,将方程组(2.10)的第二式两端乘,再将第一式代入,得到:
(2.14)
方括号内的部分记为积分核函数,对于三维问题,它是一个矩阵(一般情况下是矩阵),即:
(2.15)
其中的表示在时间区域上的积分。这个矩阵并不是对称矩阵,但仍满足如下关系:
(2.16)
矩阵形式的积分核函数称为矢量场的空间相关函数。如果将该相关矩阵的每一个元素用一个函数表示,那么式(2.16)也可以表示为:
(2.17)
此时,式(2.14)可以写为如下的分量形式:
(2.18)
其中。显然,这也是积分方程的特征值问题,是一种矢量函数特征值问题。
式(2.11)和(2.14)都属于第二类Ferdholm积分方程,核函数是正定Hermite核。这类方程的性质可以由Hilbert-Schmidt定理给出:(1)该问题的特征函数是正交的,这些特征函数使得(2.5)所定义的泛函取极小值;(2)所有特征值都是实数,并且是非负的,因此,特征值是有意义的;(3)流场在M充分大时,可以通过特征函数完全重构出来。
综上在已知脉动速度场后,首先根据式(2.12)得到时间相关函数,计算该相关函数的特征值和相应的特征函数。这个特征函数称为时间特征函数,或者时间模态。原则上说,特征值和特征函数都有无穷多个,可以将特征值按从大到小的降序排列,然后仅考虑前M个较大的特征值和对应的特征函数。同时又事先要求特征函数的范数都是单位值,以及特征函数都是正交的,即:
(2.19)
也就是说,找到了使得(2.11)成立。再利用方程组(2.10)的第二式,可以给出函数的表达式:
(2.20)
其中。利用是时间相关矩阵特征函数,并且特征值是这一性质,可以证明的正交性:
可见,所得到的就是一组单位正交基。从展开式(2.4)可以给出系统在时刻t的脉动动能
(2.21)
其中
(2.22)
代表了速度场在第j模态上的能量,因此其实就是一种能谱。从上式也看出特征值的物理意义,它代表了整个时间范围内,第j阶模态上的总能量
(2.23)
也就是说,绘制特征值的分布,其实也就是给出了一种能谱。
2.1.2 速度场是离散函数的情况
由于实际流场空间点是离散的,时间序列也是离散的,因此有必要将上述的推导从连续场转换到离散场。
总结上一节的推导,POD方法利用函数和将流场表示成式(2.4)的形式。根据式(2.12)得到的时间相关函数,可以获得特征值和相应的特征函数,最后再根据式(2.20)获得函数。
假设流场的空间离散为N个点,即;时间序列离散为M个点,即。因此可以将速度场表示为离散形式:
(2.24)
其中的每一列表示某一时刻流场各个空间点的速度信息,速度场和也可以用相似的形式表示。
由于速度场是离散的,因此对于空间坐标x的积分和对于时间坐标t的积分,可以采用某种数值积分公式。例如对于时间坐标的积分,可以表示为
(2.25)
其中,这里的是和时间步长以及积分方法相关的权函数,通常是正的,表示大的正函数值对积分总是有更大的正贡献。但是为了简化考虑,暂时忽略权函数的影响。同样地,对于空间坐标的积分也可以用相似的数值积分方式进行处理。
根据以上假设,将式(2.12)表示为离散形式,即
(2.12)
(2.26)
也可以用矩阵的形式表示,即
(2.27)
即
那么式(2.11)也可以表示为
(2.11)
(2.28)
也可以用矩阵的形式表示,即
(2.29)
因此求解特征值和特征函数,相当于求解矩阵C的特征值,即
(2.30)
其中,
最后再根据式(2.20)获得函数,即
(2.20)
(2.31)
上式也可以用矩阵形式表示,即
即
(2.32)
其中。
也可以写成分量形式
(2.33)
综上所述,经过计算获得了函数,以及特征值。从而可以获得式(2.4)表示的流场分解形式。
(2.4)
矩阵离散形式可以表示为(简便起见,只表示了的分解形式,是类似的形式)
(2.34)
因此,称为POD模态,与空间坐标相关;t),表示为模态在t时刻的模态系数,与时间坐标相关。这里可以说明一点,数据矩阵的每一列都可以用数据序列线性表示。也就是说,可以认为数据序列表示的空间结构为不同时刻流场数据所共有的特征,包含了流场中比较重要的信息,因此令此序列为POD模态。同时,在数据处理过程中,将的值按照从大到小排列,也即越靠前的模态,所占流场能量的比例越高。
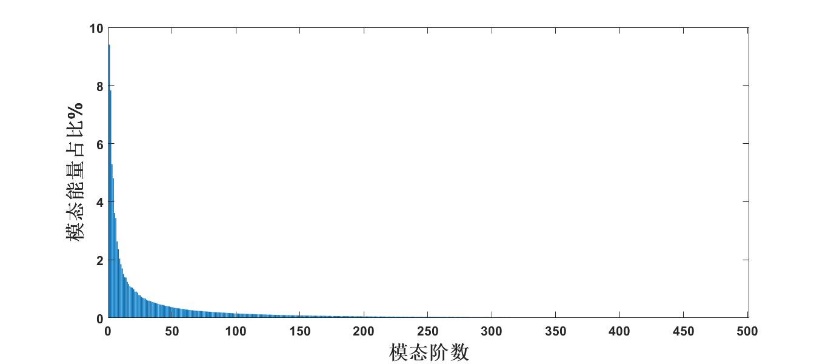
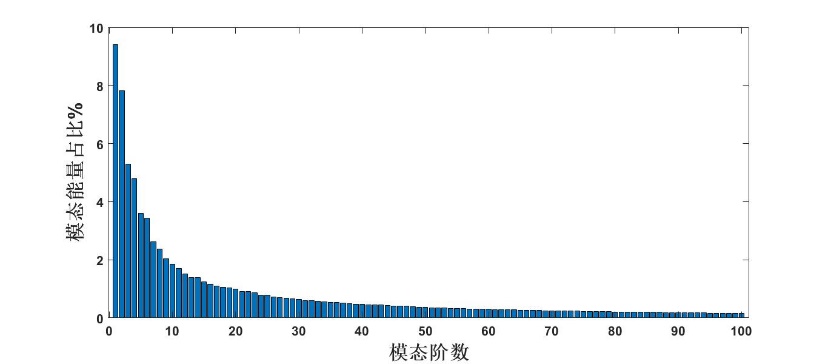
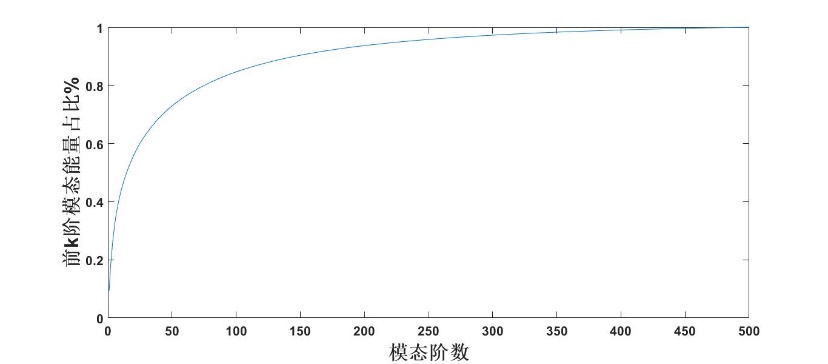
根据之前的推导,特征值代表了整个时间范围内,第j阶模态上的总能量。因此可以定义前k阶模态对流场能量的贡献,即
(2.35)
2.2 DMD方法原理
2.2.1 DMD原理推导
DMD方法是一种从数值模拟或者实验数据序列中,提取具有单一频率拟序结构的数据处理方法。
首先从数值模拟或物理实验中获得一系列流场数据,并形成一个数据矩阵,此矩阵的构造方法与附录A描述的过程一致。此外,假设数据是随时间均匀提取的,时间步长为。那么可以获得如下数据序列
其中每一个都是一个复向量,有M个分量(测量点),即
接下来从流场数据序列中构造下述两个数据矩阵:
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: