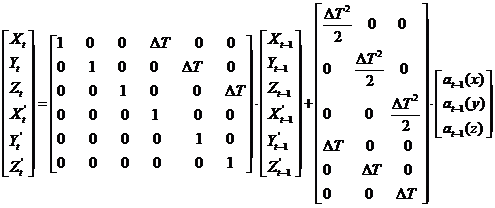基于鲁棒EKF的水下机器人目标跟踪算法毕业论文
2020-02-19 09:06:35
摘 要
随着海洋资源重要性的提高,在海洋资源利用领域扮演着重要角色的水下机器人越来越受到世界各国的重视。目标跟踪技术对于实际运用的水下机器人来说是必不可少的,对于目标跟踪技术来说,得到目标精确的位置信息是其中的关键所在。而滤波就是一种从包含误差的信号中得到目标精确的位置信息的技术。本文研究的便是一种基于鲁棒EKF的水下机器人目标跟踪算法,鲁棒EKF是一种基于经典卡尔曼滤波的适用于非线性的滤波技术。本文通过对水下机器人进行数学建模,给出了实现EKF算法的鲁棒性的方法。分别运用了卡尔曼滤波,普通EKF,鲁棒EKF对该模型产生的位置信息进行滤波处理,并对三种滤波算法的结果进行了对比分析,得出了如下结论:
1)经典卡尔曼滤波在线性系统滤波效果良好,能过显著降低目标信息的误差,但当目标系统变为非线性系统时其滤波效果便会大大降低。
2)扩展卡尔曼滤波在非线性目标系统中的滤波性能要远远好于卡尔曼滤波。
3)在对于水下机器人位置信息的滤波处理过程中,鲁棒卡尔曼滤波的效果要优于扩展卡尔曼滤波。
关键词:卡尔曼滤波;扩展卡尔曼滤波;水下机器人;非线性;鲁棒性
Abstract
With the improvement of the importance of marine resources, underwater robots, which play an important role in the field of marine resources utilization, have been paid more and more attention by all countries in the world. Target tracking technology is indispensable for the practical application of underwater robots. For the target tracking technology, the key is to obtain the accurate location information of the target. Filtering is a technique to obtain accurate location information from signals containing errors. In this paper, a robust EKF-based target tracking algorithm for underwater vehicles is studied. Robust EKF is a filtering technique based on classical Kalman filter for non-linearity. In this paper, a method to realize the robustness of EKF algorithm is given by mathematical modeling of underwater vehicle. Kalman filter, ordinary EKF and robust EKF are used to filter the location information generated by the model. The results of the three filtering algorithms are compared and analyzed. The following conclusions are drawn:
1) The filtering effect of classical Kalman filter in linear system is good, which can significantly reduce the error of target information, but when the target system becomes a non-linear system, its filtering effect will be greatly reduced.
2) The filtering performance of extended Kalman filter in nonlinear target system is much better than that of Kalman filter.
3) In the process of filtering the position information of underwater vehicle, the effect of robust Kalman filter is better than that of extended Kalman filter.
Key words: Kalman filter; Extended Kalman filter; Underwater vehicle; Nonlinearity; Robustness
目录
中文摘要 I
Abstract II
第1章 绪论 1
1.1研究背景 1
1.2国内外的研究现状 1
1.3本文研究内容与技术路线 4
第2章 卡尔曼滤波算法 5
2.1卡尔曼滤波 5
2.1.1卡尔曼滤波简介 5
2.1.2 卡尔曼滤波方程 5
2.2 卡尔曼滤波流程 7
2.2.1 滤波计算流程 7
2.2.2 滤波工作流程 7
2.3 卡尔曼滤波目标跟踪应用与仿真 9
2.3.1 水下机器人运动模型建立 9
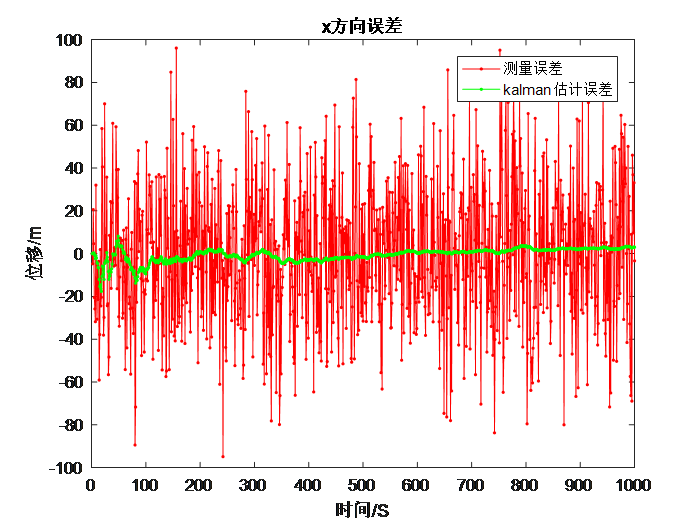
2.3.2 误差对比 11
2.4 本章小结 14
第3章 扩展卡尔曼滤波 15
3.1 扩展卡尔曼滤波原理 15
3.1.1 扩展卡尔曼滤波简介 15
3.1.2 扩展卡尔曼滤波原理介绍 16
3.2 EKF仿真实验 17
3.3 本章小结 18
第4章 鲁棒扩展卡尔曼滤波 19
4.1 鲁棒EKF简介 19
4.2 鲁棒EKF原理 19
4.3 鲁棒EKF算法流程图: 21
4.4 本章小结 22
第5章 算法仿真与结果分析 23
5.1水下机器人运动模型建立 23
5.2 仿真值设定 24
5.3 仿真结果分析 25
5.4 本章小结 25
第6章 总结与展望 27
6.1 总结 27
6.2 展望 28
参考文献 29
致谢 31
附录 32
第1章 绪论
1.1研究背景
海洋占地面积极广,其在人类的生存与发展的过程中扮演着极其重要的角色。海洋中蕴含着许多对人类发展有极大作用的珍稀资源。进入二十一世纪以来,人类社会的科学技术在飞速地进步,但于此同时陆地上的资源也在人们的开采下急剧地被消耗。因此,海洋中包含的资源的价值也越来越被人们所重视,海洋开发成为了当今各国发展的重要途经。但由于海洋环境的特殊性,其资源的开采难度远大于陆地资源,仅仅依靠人力难以实现海洋资源的合理利用。为此水下机器人技术应运而生。水下机器人可以代替人工在被汽油,毒品等污染物污染过的,非常危险的水下环境甚至是可见度为零的水域长时间作业,具有非常强的工作能力。于此同时,水下机器人在科学研究、海洋资源勘探、打捞救生以及军事等领域也得到了广泛应用[1]。目前水下机器人在人类的发展过程中已经占据了一席之地。因此水下机器人技术已经为了新世纪各个国家不可或缺的一项重要技术[2]。
而在水下机器人相关技术之中,目标跟踪技术乃是不可或缺的重要一环。目标跟踪技术对于水下机器人实现避障、导航、水下信息探索等功能都有着不可或缺的作用。[3]除此之外,由于水下运动物体有可能是我们感兴趣的目标或者成为水下机器人的潜在威胁,因此对运动物体进行准确有效的跟踪对于帮助水下机器人更好地完成自身的任务以及确保其安全航行都有着极其重要的作用。而目前,由于水对光电等信号的传播都有较强的削弱作用,而声波信号在水中的传播则表现良好,而且lars通过结合声探测特点提出了一种快速的区域跟踪方法,验证了利用声探测手段实现水下目标跟踪的可行性[4] 。因此基于声纳的探测手段成为了目前水下机器人进行目标探测的主要手段[5]。但是由于声纳的探测精度并非很高,且由于海洋环境的影响,设备的噪声统计特性(平均值和方差)未知。这使得进行准确的估计变得异常艰难。而且在目标跟踪中,通常以目标的位置矢量和速度矢量作为状态向量,观测方程中目标方位与位置矢量为三角函数关系,因此其观测方程具有很强的非线性。,这就给滤波算法的解决问题带来了很大困难,因此进行精确滤波算法相关的研究对水下机器人的目标跟踪技术具有重要意义。
1.2国内外的研究现状
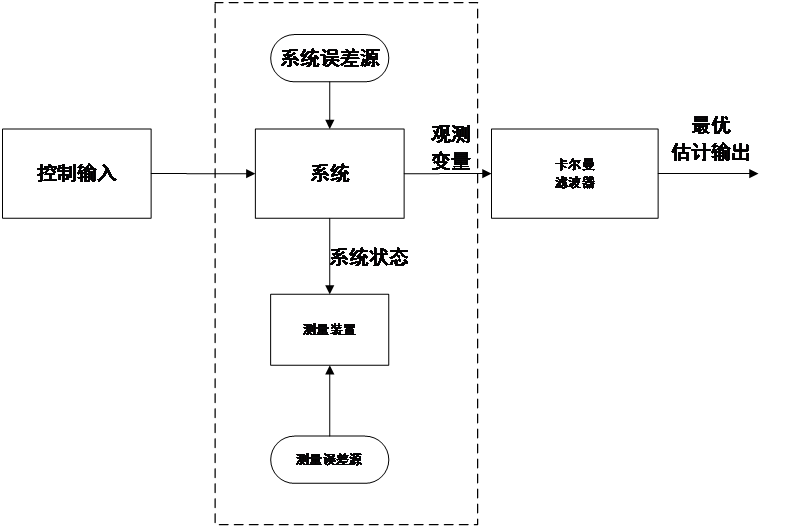
从本质的层面来分析,滤波过程就是对信号进行处理与变换的过程, 而这一过程在目前来说有两种实现方式,其一是硬件的方法,其二便是软件的方法[6]。而滤波算法正是在软件层面上实现滤波过程的方法。对于滤波算法来说主要可以分为两大类, 一类是线性系统,一类是非线性系统。对于线性系统来说,国内外学者早已做了大量的研究。在第二次世界大战期间,美国控制理论大师维纳提出来维纳滤波。而提出维纳滤波的最初目的是为了解决火炮对空的控制问题。因此此项技术在当时属于美国国家机密,所以一直到解密期限到了,维纳才对外公布维纳滤波原理。维纳滤波是一种频域的方法,这就导致其只能处理那些较为安稳的时间序列的滤波和预测问题。而且由于在维纳滤波的过程中涉及到复杂的方程求解,而且其算法是非递推的,这也就要求在使用维纳滤波的过程中必须要保留所有的历史数据,这就对储存空间的大小提出了很高的要求,而这一点对于工程领域来说是极为不方便的[7]。正是由于维纳滤波原理的这些天然劣势妨碍了其在工程上发挥作用,世界各地的学者都在寻求着更为方便的滤波方法。
随着时间的推移,计算机被研发出来并得到了飞速地发展,处理多维实时数据成为人们的需要,因此人们迫切地需要一个能够替代维纳滤波的滤波方法。卡尔曼滤波器在学者们的渴求下被提了出来。卡尔曼在十九世纪中叶首次提出了卡尔曼滤波,在该项技术中卡尔曼教授创新性地提出了了状态空间这一概念,在卡尔曼滤波方法中,系统的状态信息可以用空间的一个向量来表示,系统下一时刻的状态可由上一时刻的最优估计预测,再通过滤波增益调节预测值和观测值便可得到系统这一时刻的最优估计[8]。这种滤波方法克服了维纳滤波的许多弊端。Kalman滤波器既可以应用于对一维系统进行状态估计,也同样可以用于二维甚至更高维度的系统。而且卡尔曼滤波器在工作过程中只需要系统上一时刻的状态和当前的实测值,这相比于维纳滤波来说节约了很多的硬件储藏空间。因此在计算机上很容易便可实现卡尔曼滤波器。由于其与维纳滤波相比有很大的优势,卡尔曼滤波器一经提出,便得到了很高的认可,并且被美国航天局选中,为阿波罗登月计划提供了控制方法。在卡尔曼滤波之后,学者们为了更好地对线性系统进行滤波,又提出了平方根滤波,奇异值分解滤波等[9]线性滤波方法。
但是上述的滤波方法毫无疑问都只能用于线性系统之中。由于水下目标跟踪问题本质上都是非线性系统 ,因此上述的所有滤波方法都不能胜任。在实际的工程实践中,对于非线性系统而言,目标的后验概率函数无从得知,所以想要得到非线性系统的最优估计无异于纸上谈兵。因此在实际运用中,作用在非线性系统上的滤波算法全都无法得到最优估计,只能得到次优估计。
对非线性滤波技术的迫切需求,科学家们在非线性领域做了大量的研究,得到了许多优秀的非线性滤波算法。其中,Unscented卡尔曼滤波器(UKF)是一种表现很好的非线性滤波算法,其运用样本点的方法来近似估计后验概率密度,但是该滤波方法对于后验概率密度不是高斯分布的系统来说,滤波结果表现得很差[10]。在国内潘泉等人对UKF有较深入的研究[11]。而粒子滤波算法(PF) 最早是由Metropolis等人提出的蒙特卡罗方法(Monte Carlo method)[12]。该滤波方法独立于系统的模型,与模型是否线性、是否高斯无关,因此,粒子滤波在强非线性系统中表现优于EKF。但同时其计算量也远远超过了EKF,在国内,杨小军等人对非线性环境下的粒子滤波算法应用作了研究总结。[13]容积卡尔曼滤波器是一种最近才开始出现的一种滤波方法,由Arasaratnam等于2009年在UKF的基础上提出来[14],该方法一经提出便得到了很高的认可,广大学者将其应用于导航,混合滤波等领域。其滤波过程与无迹卡尔曼滤波有很多相似之处,只不过与UKF比起来,CKF的数学理论推导更加严谨。该滤波方法是国内外研究的热门。国内,胡玉梅,等人对CKF也有一定研究[15][16][17]。而在非线性滤波算法中,EKF毫无疑问是最为经典的非线性滤波算法[18],该滤波算法通过泰勒展开将目标系统状态函数简单线性化,将其转化为线性系统,线性化后的滤波流程与KF基本一致。由于其变换手段的限制,EKF是一种次优估计,其运用在非线性不强的系统上的效果非常好,而在其他情况表现并不好。[19] EKF在算法层面上实现起来比较简单,只需要在卡尔曼滤波算法的框架里面加上线性化的过程即可。但当目标系统的非线性增强或者系统中的噪声不是高斯分布时,其工作性能便会变差甚至出现滤波发散。EKF与现在最新的非线性滤波算法相比有很多不足之处,但其作为经典的卡尔曼滤波推广形式,在现在的很多滤波算法中都可以找到它的影子,因此对扩展卡尔曼滤波进行研究和算法的实现对于新算法的提出和实现都有很大的帮助作用。
对上述的各种滤波算法大概总结如下图:
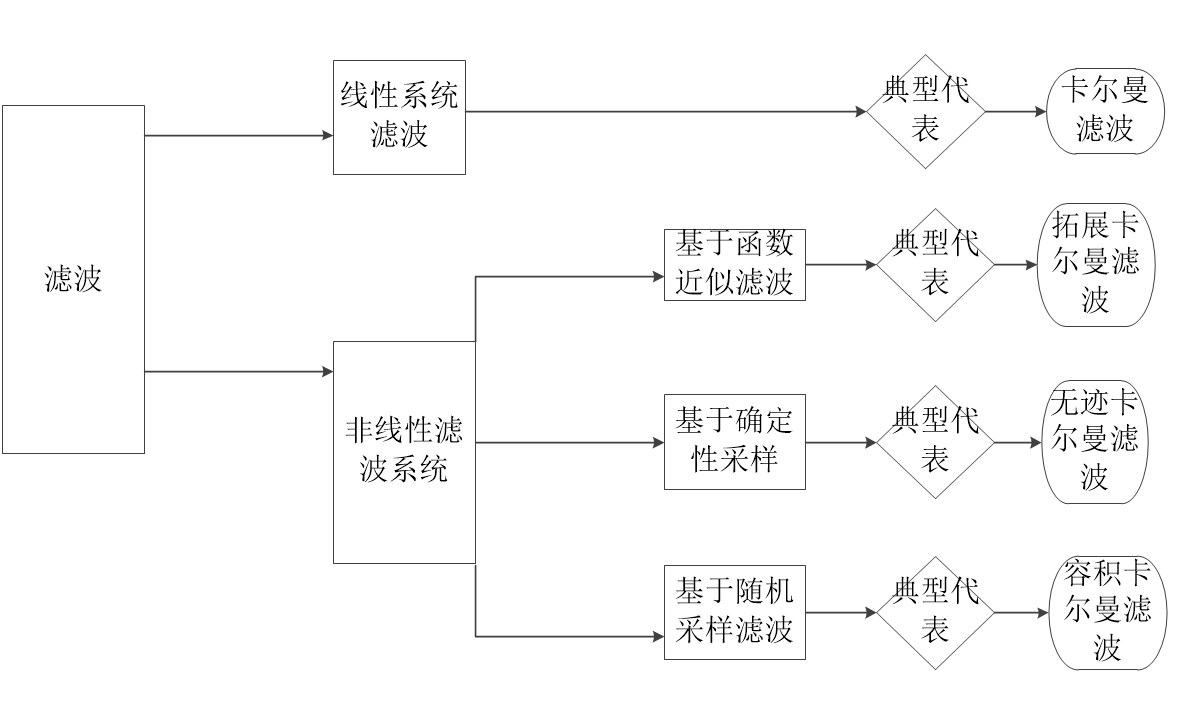
图1.1 滤波算法总结

1.3本文研究内容与技术路线
本文主要的研究内容是基于水下机器人的鲁棒扩展卡尔曼滤波算法。在现在的工程领域,扩展卡尔曼滤波仍然经久不衰,在各个领域发光发热。这一切都证明了Extend卡尔曼滤波的强大之处,但同时本文将通过建立数学模型的方法模拟得出水下机器人在水下的一系列状态数据,在对其加上高强度噪声后分别运用传统卡尔曼滤波,传统扩展卡尔曼滤波以及具备鲁棒性的扩展卡尔曼滤波对被噪声干扰的数据进行处理,以此来验证鲁棒性对扩展卡尔曼滤波的优越性。具体的工作内容如下:
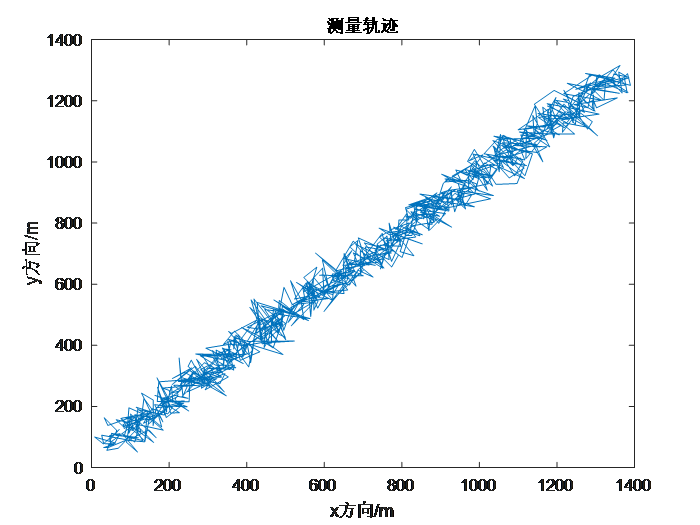
(1)首先通过建立数学模型的方法得到水下机器人在直角坐标系下的位置坐标和各项数据,然后通过对数据进行处理得到球坐标系系的位置坐标和数据,并且在转换过程中通过数学方法模拟噪声的产生以符合真实情况。以上即为对声纳采集数据的模拟。
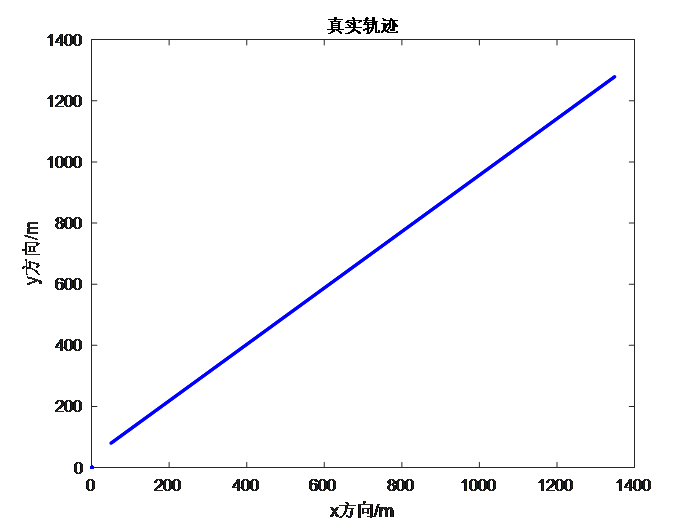
(2)在完成数据的采集之后,通过MatLab软件对真实数据和测量数据进行绘图,得出噪声对真实数据的巨大影响,从而得出在现实的工程领域对测量数据进行的滤波处理的必要性,以及滤波的重要性。
(3)运用卡尔曼滤波对线性系统的位置数据进行滤波处理,并且以图的形式将滤波后的数据与滤波前的数据进行对比,从而展现出经典卡尔曼滤波的突出优点。
(4)介绍扩展卡尔曼滤波,并且详细给出扩展卡尔曼滤波的公式推导和算法流程图,并通过分析具体案例得出扩展卡尔曼滤波的优点以及缺点。
(5)引出鲁棒扩展卡尔曼滤波,同时运用经典卡尔曼滤波,扩展卡尔曼滤波以及具有鲁棒性的扩展卡尔曼滤波对上述步骤1得到的数据进行滤波处理。最后对三种滤波方法的结果进行对比,得出三种算法的优劣。
第2章 卡尔曼滤波算法
2.1卡尔曼滤波
2.1.1卡尔曼滤波简介
1961年卡尔曼发表了一篇论文,在该论文他创造性地引入了状态空间这一概念,并在此基础上提出一种在测量方程和系统状态方程基础之上运用递推计算进行估计得到最优估计值的一种滤波算法,这便是卡尔曼滤波算法。该方法一经提出便取得了了很高的认可度。
在卡尔曼滤波问世之前,工程领域普遍采用的滤波方法时维纳滤波,但是维纳滤波在应用上却显现出了很多的不足之处,卡尔曼滤波正是卡尔曼教授为了克服维纳滤波的不足而提出的一种全新的线性滤波理论,与维纳滤波只能运用在平稳的一维工程不同,卡尔曼滤波在波动性较大的多维的系统中同样适应的很好。而且,与维纳滤波相比,卡尔曼滤波在计算机上实现起来更加方便。这对于当时的控制领域来说无疑是很受关注的,很快卡尔曼滤波便成功地应用于阿波罗登月,并在之后被广泛运用于各个工程领域。
2.1.2 卡尔曼滤波方程
下面给出的是线性离散系统下的基本卡尔曼滤波流程,而再给出具体流程之前须知卡尔曼滤波的应用须有如下几个必要的条件。这些条件包括:首先,由于卡尔曼滤波是线性算法,因此系统的测量方程以及预测方程都必须是线性的。其次,状态噪声和量测噪声应该都是零均值高斯白噪声。再有,状态噪声,量测噪声以及目标的状态这三者之间应该是无关的。最后,滤波对象的初始值或者其统计特性必须是已经知道的。只有当上述几个条件都满足的情况下,所得到的滤波结果才会是最优估计,否则估计结果的最优性无法保证。
在满足上述条件的情况下,下文将给出卡尔曼滤波的滤波过程。本文对其具体的数学推导过程不做研究。
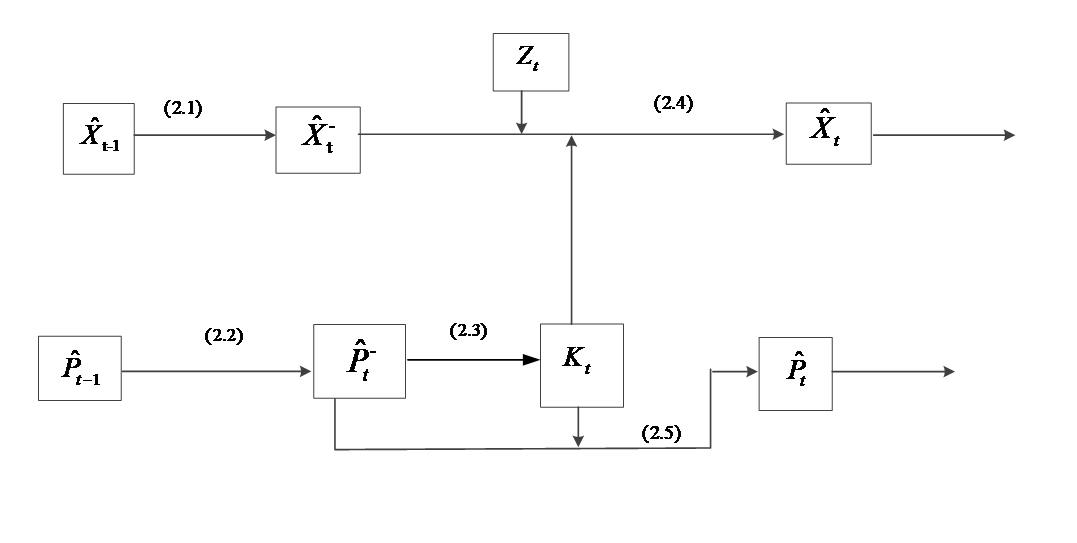
第一步 状态预测。公式如下
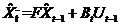 (2.1)
(2.1)
在该过程中,系统利用上一时刻的状态信息的最优估计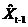 计算得到系统这一时刻的预测值
计算得到系统这一时刻的预测值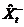 。该值为中间量,并非滤波的最终估计结果。
。该值为中间量,并非滤波的最终估计结果。
第二步 预测状态协方差矩阵。预测公式如下
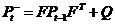 (2.2)
(2.2)
公式(2.2)中, 表示的是在对系统t-1时刻的状态信息进行估计时由于与系统实际变化有差别而产生的误差,而
表示的是在对系统t-1时刻的状态信息进行估计时由于与系统实际变化有差别而产生的误差,而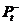 则是对t时刻误差的估计量,此值也只是中间量,并非结果。Q为该预测过程的误差。
则是对t时刻误差的估计量,此值也只是中间量,并非结果。Q为该预测过程的误差。
第三步 求解滤波增益矩阵,求解公式如下
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: