摘 要

无轴轮缘推进器是一种先进的新型电力推进器，它采用螺旋桨与电机一体化思想，它具有解放机舱空间、高效节能和减振降噪等显著优点。该推进器采用完全水润滑轴承系统，其中水润滑推力轴承需要承担螺旋桨产生的推力，它是无轴推进器的关键部位。但由于无轴推进器水润滑推力轴承工况恶劣，例如低速、重载、泥沙等因素，普通斜面固定瓦推力轴承难以形成足够的承载力，研究表明在瓦面开螺旋槽是提高轴承承载能力的有效途径，为此本文将螺旋槽引入到水润滑推力轴承中，通过研究不同结构参数对轴承性能影响规律，为无轴推进器推力轴承设计提供依据。

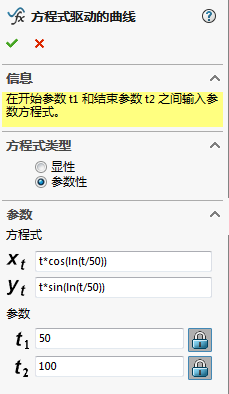
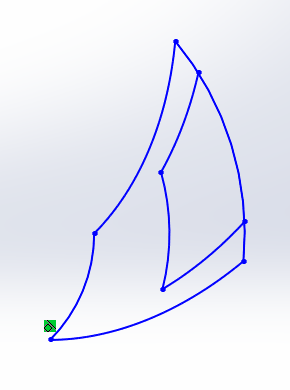
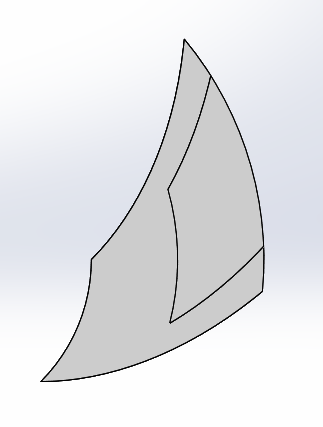
本文首先设计了一个内径为50mm，外径为100mm的轴承，其螺旋槽型线为对数螺旋线，并周期性地围绕轴承轴心线分布在表面。由于推力轴承主要靠轴承间隙中的水膜产生流体动压来承担载荷，对此本文利用Soliworks设计了一个最小膜厚为50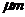的单块水膜，并借助ICEM对其划分网格，之后用FLUENT对该水膜进行数值模拟，得到了水膜的压力分布图、速度分布图以及承载性能随不同工况参数的变化规律，同时运用该方法对一长为100mm，宽为125mm的矩形可倾瓦推力轴承瓦块进行仿真计算，得到的值与解析解进行比较，论证了本文研究方法的合理性。最后通过改变螺旋槽平面型线、槽深和槽宽比等结构参数，分析其对推力轴承性能的影响规律。

研究发现采用阿基米德螺旋线型的螺旋槽可以提高轴承承载力，但轴承工作平稳性降低。而当轴承间隙一定，把槽深与轴承间隙的比值控制在2左右；或当轴承间隙为3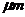0~70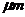，将槽深控制在100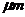左右，轴承承载性能均可保持较高水平。另外增大槽宽比，可以提高轴承承载性能，且对轴承工作的平稳性无较大影响。

关键词：无轴推进；推力轴承；螺旋槽；水膜；数值模拟；

Abstract

Shaftless rim-driven propeller is an advanced new electric propeller. It uses propeller-motor integration design idea. It owns the remarkable advantages of liberating engine room space, high efficiency and energy saving, vibration reduction and noise reduction. The propeller adopts a full water lubricated bearing system, in which the water lubricated thrust bearing needs to bear the thrust produced by the propeller. It is the key part of the shaftless rim-driven propeller. However, because of the bad working conditions of the water lubricated thrust bearing, such as low speed, heavy load and silt, the bearing capacity of the thrust bearing with ordinary inclined fixed tile is difficult to form. The research shows that the spiral groove on the tile surface is an effective way to improve the bearing capacity of the bearing. Therefore, the spiral groove is introduced to the water lubricated thrust bearings in this paper. In order to provide design direction of the thrust bearing of shaftless propeller, the influence law of different structural parameters on bearing performance is studied.

In this paper, a bearing with an inner diameter of 50mm and an outer diameter of 100mm is designed. The shape of spiral groove is logarithmic spiral line, and the groove is periodically distributed around the axle center line of the bearing on the surface. Because the thrust bearing mainly depends on the hydrodynamic pressure of the water film in the bearing clearance to bear the load, a single water film with a minimum film thickness of 50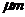 is designed by Solidworks, and the mesh is divided by ICEM. Then the water film is simulated with FLUENT, and the pressure distribution map and velocity distribution map of the water film are obtained. As well as the variation law of the bearing performance with different working conditions, the method is used to simulate a rectangular tile of the tilting pad thrust bearing with a length of 100mm and a width of 125mm. The value of this method is compared with the analytical solution, and the rationality of the study method is demonstrated. Finally, by changing the structural parameters such as the shape of the spiral groove, groove depth and groove width ratio, the influence on the performance of thrust bearing are analyzed.

It is found that the bearing capacity can be improved by using spiral groove with shape of Archimedes spiral line, but the working stability of bearing is reduced. When the bearing clearance is certain, the ratio of the groove depth to the bearing clearance is controlled to about 2, or when the bearing clearance is 3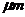0~70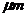, the groove depth is controlled at about 100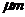, the bearing capacity of the bearing can be maintained at a high level. In addition, increasing the groove width ratio can improve the bearing performance of the bearing and has little effect on the stability of the bearing.

Key Words：Shaftless propulsion；thrust bearing；spiral groove；water film；

Numerical simulation；

目 录

摘 要 I

Abstract II

第1章 绪论 1

1.1 研究的背景及意义 1

1.2 国内外研究进展及现状 1

1.3 本课题研究的主要内容 5

第2章 计算流体力学基本理论 8

2.1 建立流体力学基本方程组 8

2.1.1 质量守恒方程 8

2.1.2 动量守恒方程 9

2.2 湍流数值仿真 9

2.2.1 湍流基本方程 9

2.2.2 湍流模型 11

2.3 离散控制方程 11

2.3.1 有限体积法 11

2.3.2 离散格式分类 12

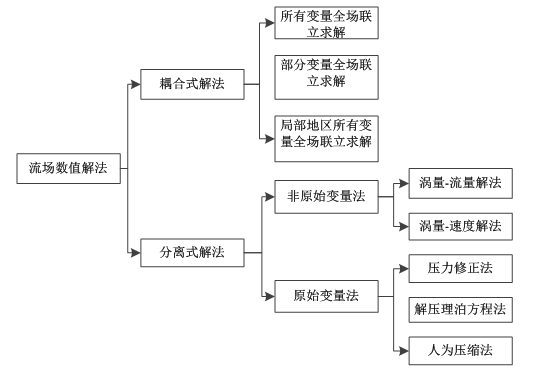
2.4 计算流体力学数值解法 13

2.5 本章小结 14

第3章 基于Fluent螺旋槽推力轴承性能仿真 15

3.1水润滑螺旋槽推力轴承简介 15

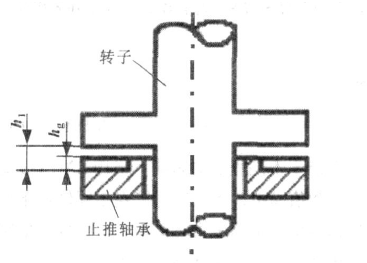
3.1.1推力轴承结构及工作原理 15

3.1.2 推力轴承主要性能参数 17

3.2 水润滑螺旋槽推力轴承水膜模型建立 17

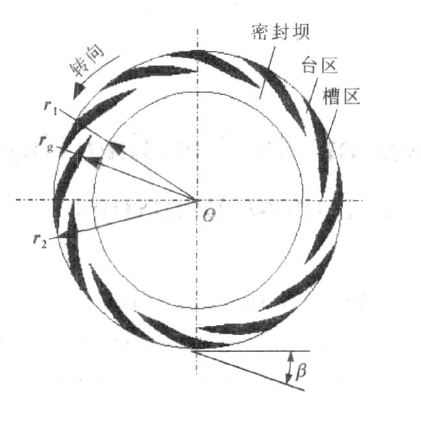
3.2.1几何模型 18

3.2.2数学模型 21

3.3计算域及网格划分 22

3.3.1网格的分类 22

3.3.2网格的划分 23

3.4推力轴承水膜数值计算 26

3.4.1边界条件的确定 26

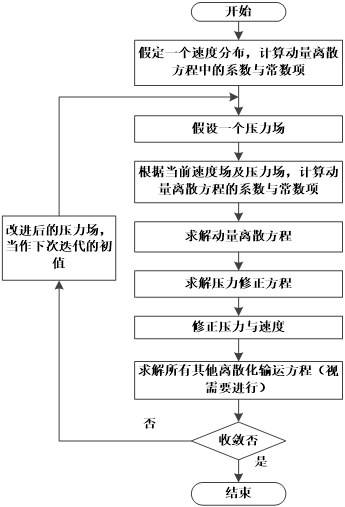
3.4.2 Fluent计算步骤 27

3.5本章小结 30

第4章 计算结果分析与方法验证 31

4.1 数值计算结果分析 31

4.1.1后处理 32

4.1.2不同工况参数的影响分析 34

4.2 研究方法的验证 36

4.2.1几何模型建立 36

4.2.2数值计算 38

4.2.3计算结果分析 39

4.3本章小结 41

第5章 不同结构参数对螺旋槽推力轴承性能的影响规律 42

5.1螺旋槽平面型线 42

5.1.1计算结果与分析 42

5.1.2 结果对比与优化方向 48

5.2 槽深 50

5.2.1计算结果与分析 50

5.2.2 结果对比与优化方向 56

5.3槽宽比 58

5.3.1计算结果与分析 58

5.3.2 结果对比与优化方向 64

5.4本章小结 66

第6章 结论与展望 67

6.1 本文总结 67

6.2展望 68

参考文献 69

致 谢 71

第1章 绪论

1.1 研究的背景及意义

无轴轮缘推进器是一种先进的新型电力推进器，将推进器和电动机合为一个整体，它拥有能够扩大机舱的容量、很大程度上节约能源以及改善工作环境等显著优点。该推进器采用完全水润滑轴承系统，包括水润滑径向轴承和水润滑推力轴承。螺旋桨桨叶在旋转时给水轴向的作用力，而水对螺旋桨桨叶也产生轴向的反作用力，该作用力驱使船舶前进，这当中水润滑推力轴承用来承受该作用力，然后将该力继续传递到船体上，它是无轴推进器的关键部位。

一般形式的推力轴承主要由推力环、推力块和推力盘等组成，它是利用流体运动产生的压力进行工作的，其中推力块相对它的一条边旋转一个较小的角度，使得推力块与推力环之间形成逐渐变小的空间，它的工作原理是通过高速旋转的推力环把流体带入到该逐渐减小的空间，在流动过程中流体因空间变小被迫挤压，从而在内部产生反抗该挤压的力,随后推力环的推力通过该空间内的流体传递到推力块上，再经过支持刃传递到调节圈上。当该空间内的流体产生的反抗力与轴向载荷相等时，轴承即为固定工作状态，在推力块与推力环的之间就形成了稳定的动压水膜，迫使两表面相互分开，摩擦形式转变为液体摩擦。推力增大时，推力块与推力环间的间隙减小，液体动压变大，传递的推力随之增大。该轴承因摩擦力做功而产生的能量损耗小，可以承受较大负荷，工作稳定性可靠。但由于无轴推进器水润滑推力轴承工况恶劣，例如低速、重载、泥沙等因素，对于一般形式的推力轴承而言，单单依靠推力环与推力块之间形成的楔形空间所产生的动力水压不足以承受相应的载荷，可能无法适应这样的工作环境。因此，有人提出螺旋槽推力轴承结构形式。

为了使推力轴承的流体动压效应加强以适应恶劣工况，在台座上加工出一些收缩的槽，利用这样的形式来形成具有更强流体动压效应的流体膜，从而进一步提高推力轴承的承载能力，与其它类型相比，该轴承润滑剂泄漏少、所受阻力小、承载力高、工作稳定^[1]。而对于螺旋槽推力轴承而言，其自身就有许多可以改进的地方，螺旋槽的平面型线结构，槽的尺寸大小等都是影响该推力轴承性能的重要因素，设计合适的螺旋槽结构形式能够极大地提升其承载能力和润滑性能。

1.2 国内外研究进展及现状

关于流体动压润滑理论的研究，最先在国外展开。早在1885年，托尔在其研究试验中发现流动的流体在遇到阻力或其他因素阻碍其流动时，会在其自身内部产生反抗力。而在1886年，Osborne Reynolds便依照托尔的实验结论，在他研究的基础上，运用流体力学的相关内容得出了流体流动的普遍方程——雷诺方程，由此解释了流体动压润滑是如何产生的，为后续流体润滑理论的研究打下了坚实的基础。

在20世纪30年代以前，因计算机的发展水平及科学计算方法还不够成熟，而求解雷诺方程需要进行大量的计算，在当时那个年代是不可能完全解出的，所以为了能够在一定程度上求解雷诺方程，许多学者在有些方面做出一些假设，简化了雷诺方程的求解条件，根据得到的雷诺方程的解析解来讨论轴承的工作特性。例如，Ocvirk和Dubois就曾做出稳定运转条件的假定，并在该条件下获得无限短轴承和长轴承的解析解^[2]。在这之后，由于计算机科技的快速发展，流体润滑理论广泛采用数值计算方法进行研究，许多学者计算了在稳定和不稳定状态下轴承的动压润滑特性以及在各种油膜不完整边界情况下有限宽轴承的数值解。

1.2.1推力轴承研究进展及现状

在关于动压轴承轴心轨迹的研究中，有两种具有代表性的方法：一种是由德国的Hahn提出的Hahn法^[3]，另一种是德国的Holland提出的Holland法^[4]，前者是将瞬间平衡态形式的雷诺方程划分为收敛和压缩两种类型，由边界条件相应算出各类型润滑膜对应的分力，然后根据矢量相加原理合成总的润滑膜压力，最后在总润滑膜压力与外载荷相等的条件下求出轴心的运动轨迹；后者是在前者的基础上，每一部分单独求解，互不干扰，计算出轴心对应的微分方程并据此算出轴心的运动方式。在此基础上，美国的Booker^[5]则发明了一种全新的轴心偏移数值法来获得轴心运动轨迹。在这之后，Dowson^[6]推导出了一种普遍形式的雷诺方程，该方程将润滑膜粘度和密度在其厚度方向上的变化考虑进去。随后他和Hudson^[7]一同提出了热流体动力分析理论，即THD，该方法进一步考虑了温度对流体粘度的影响，另外还将推力环及轴承的传导热考虑进来。

在结构方面，Singh^[8]分别研究了轴承宽度无穷大的指数、摆线、垂链形式和多项式等一维直线轴瓦面形状的润滑特性，发现以上瓦面形状可以增强轴承的承载性能，但是要想确定最有效的瓦面形状还必须根据轴承实际大小做出选择。陈志澜等人则研究二维瓦面的结构，通过建立相应的曲面模型，对柱面、阶梯面、马背面等六种表面形状异同的轴承做出三维立体热动力分析，探讨了台区膜厚、油膜压力峰值以及最高油温与瓦面形变的相关性，得到的结论为沿周向突出和沿径向凹陷的瓦面形状都可以较好地构建楔形油膜，可以明显改善轴承润滑特性^[9]。

在动特性方面，周建军对用支点固定的扇形可倾瓦推力轴承进行研究，在考虑瓦块受热发生形变以及润滑剂粘度发生改变的情况下，采用一系列方法对瓦块的运动方程、瞬间形式雷诺方程及其能量方程联立求解，得到了冲击负荷对轴承刚度的影响规律^[10]。李忠则通过构建可倾瓦推力轴承成正比和不成正比的物理模型得出油膜压力和力矩，采用偏导数法得到相应的刚度阻尼系数，并且分析了负荷、转速、油温等对轴承动特性的作用规律，发现当油膜厚度变大时，油膜承载力和刚度阻尼系数都变小^[11]。而山东大学的马向伟在推导出扰动压力方程的计算公式的基础上，研究了各结构参数对轴承动特性的影响^[12]。

在温升对润滑性能的影响方面，Ettles认为滑油是从前一个瓦块表面流过的热油和油槽里的冷油相融合后进入后一个瓦块的，瓦块温度即为热油与冷油相融合之后的温度，而且得到了滑油换热系数和进油温度的表达式^[13-16]。而Neal认为润滑油温度在其径向、周向以及厚度方向上都会产生不同，即油膜温度呈立体变化，因此进行了二维和三维热流体动力分析^[17]。李忠采用有限差分法对可倾瓦推力轴承进行二维流动分析，得出温度因素不变，油膜总体温升也几乎不变^[18]，他还与王凤才等人一同提出了一种新型瓦——螺旋面扇形瓦，将其运用到推力轴承中，发现其温升较小，热动力润滑性能较好，可以取代平面扇形瓦^[19]。

通过几十年的探讨与研究，推力轴承的研究不断得以优化和完善。但现如今仍有许多问题需要解决，这些问题总结起来主要分为两个，一个是润滑剂的模型设计方面的问题，主要在于能准确描述该流动方式的物理模型较少，因此还不能广泛普遍地采用进行研究讨论，针对此问题，只能依靠不断进行实验模拟，在其基础上建立模型并对其验证。另一个问题则是数值计算过于冗杂，虽然现如今计算机技术发展迅猛，但对于该复杂的计算过程和众多的边界条件，其计算精度有时仍不能满足要求，为了准确描述轴承润滑问题，只能依靠计算机技术的发展^[20]。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：