基于蚁群算法的一维装箱问题研究毕业论文
2020-04-05 11:01:14
摘 要
本文主要针对一维装箱问题的优化进行求解,只考虑箱子和物品的长度这一个因素,而且优化的对象都是不定长的箱子和不定长的物品。利用蚁群算法,借助于编程软件MATLAB,对基于蚁群算法的一维装箱问题进行了编程、仿真和分析。利用蚂蚁转移路径和信息素矩阵来表示箱子长度和物品长度的相互关联,并根据这一原则进行一维装箱操作优化。仿真结果表明,基于蚁群算法的一维装箱算法可以得到非常理想的最优解,而且可以明显提高箱子长度的利用率,保证了装箱操作的高效益,得到更小的冗余长度率。
关键词:一维装箱;蚁群算法;不定长箱子和物品;冗余长度率
Abstract
This paper mainly focuses on the optimization of the one-dimensional packing problem. It only considers the length of the box and the item, and the object to be solved is an indefinite box and an indefinite item. The ant colony algorithm is used to program the software MATLAB. The one-dimensional binning problem based on ant colony algorithm was programmed, simulated and analyzed. The ant transfer path and the pheromone matrix are used to represent the correlation between the length of the box and the length of the item, and the one-dimensional boxing operation is optimized based on this principle. The simulation results show that the one-dimensional packing algorithm based on the ant colony algorithm can obtain a very optimal optimal solution, and can significantly improve the utilization of the box length, ensure the high efficiency of the packing operation, and obtain less redundant length rate.
.
Key Words:One-dimensional packing; ant colony algorithm; indefinite length boxes and items; redundant length rates
目录
第1章 绪论 1
1.1 目的及意义 1
1.2 国内外研究现状 1
1.3研究内容及技术方案 2
1.3.1研究内容 2
1.3.2技术方案 2
第2章 一维装箱问题 3
2.1装箱问题概述 3
2.2一维装箱问题涉及的因素 3
2.3一维装箱问题经典算法 4
第3章 蚁群算法 6
3.1蚁群算法基本介绍 6
3.1.1算法来源 6
3.1.2算法原理 6
3.2蚁群算法概述 7
3.2.1蚁群算法概述 7
3.2.2蚁群算法的应用 8
3.3蚁群算法的特性 8
3.3.1蚁群算法的优势 8
3.3.2蚁群算法的缺点 10
第4章 基于蚁群算法的一维装箱问题研究 11
4.1蚁群算法在装箱问题中的应用 11
4.1.1蚁群的构建 11
4.1.2约束条件的讨论 11
4.1.3算法的初始化 12
4.1.4蚂蚁的一次搜索 12
4.1.5概率计算方法 12
4.1.6信息素更新方法 13
4.1.7最佳方案 13
4.2算法描述 14
第5章 实例仿真与分析 16
5.1实例数据概况 16
5.1.1实例一数据 16
5.1.2实例二数据 16
5.1.3实例三数据 18
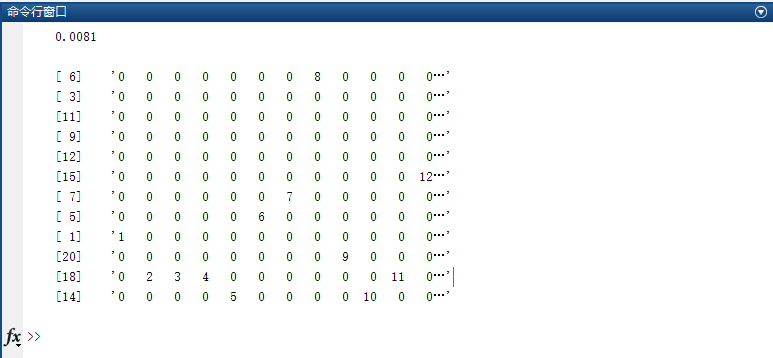
5.2实例优化效果 20
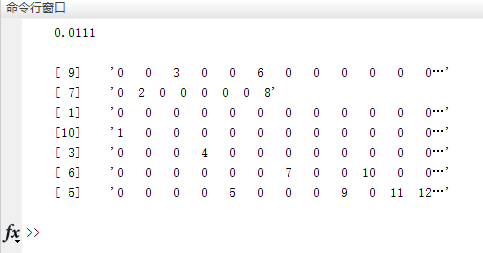
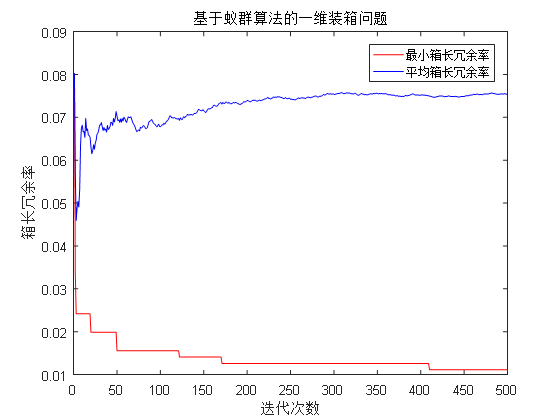
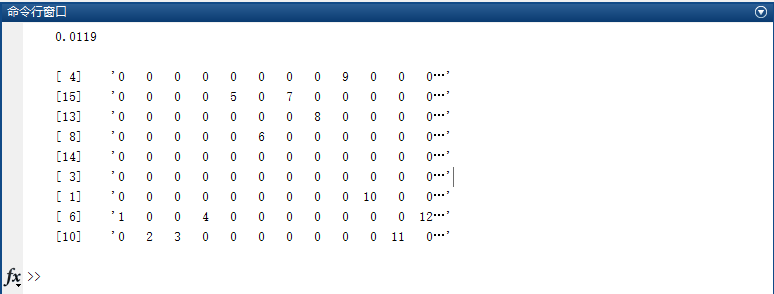
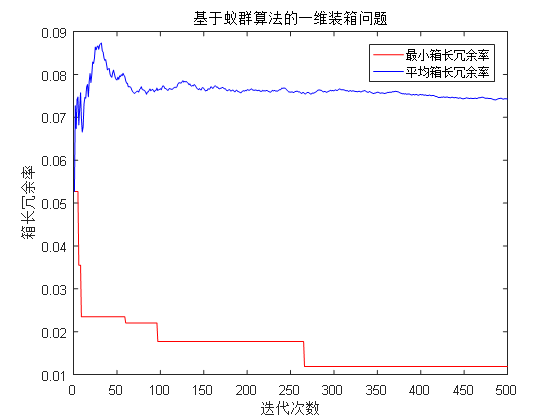
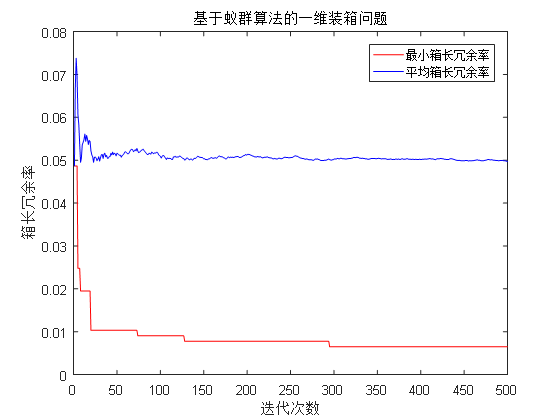
5.2.1实例一仿真结果 20
5.2.2实例二仿真结果 21
5.2.3实例三仿真结果 23
5.3应用分析 24
5.3.1参数设定对基于蚁群算法的一维装箱问题的影响 24
5.3.2应用分析 25
第6章 总结与展望 26
参考文献 27
致 谢 29
附录 30
第1章 绪论
1.1 目的及意义
装箱问题也被称为背包问题,换句话来说,就是把小物品装填到大箱子中去。要解决的问题是:在箱子容量一定的情况下,怎样装才能装更多的物品。比如说,我们日常生活中最常见的“装冰箱”问题。有一个很有意思的现象就是,当我们感觉冰箱再也装不下其他物品的时候,经过一翻折腾之后又可以装下更多的物品,在有限的容积下放入了更多的东西,最大化地利用了冰箱空间。装箱问题一般可以用大物体和小物品的几何组合来进行描述:将大的物体定义为空的,需要用小物品去装填大的物体。装箱问题最关注的一点是在装箱过程中,通过改善物品的放置次序或位置,以达到获得最大效益的目的[3]。
装箱子的问题是一种存在于我们生活之中的、十分广泛的现象。在我们社会生产的众多的行业之中,有非常多的行业面临着这个难题。比如说,我们日常生活中离不开的穿衣问题,一件衣服从原材料到一件成熟的商品时需要经过加工的,首先就面临着如何裁剪布料这一问题,如何裁剪才能得到最好的结果,布料的剪切就是一类装箱子问题。除此之外,在一些高新领域也存在着这个问题,这其中就包含了计算机科学中的信息处理问题。在对信息进行处理的时候,如何合理而高效的调用计算机资源对信息进行处理,影响着输出结果的准确性和效率。因此,这也可以看作是一种装箱问题。这样的例子还有非常的多,不胜枚举,这也从侧面说明了装箱问题的重要性和巨大的研究价值。
从我们身边的实际应用的角度来讲,装箱过程的目标通常是采用最优化的方案,最大限度的将原材料应用到生产中去。即使是非常小的优化改动,也很有可能节省大量的成本,提高总体的收益。这对大规模生产来说,具有非常重要的经济意义。从公司运营方面来讲,就是最大限度的让每个载体(仓库、车辆、集装箱、船等)承载尽量多的物品,以达到节约公司支出,提升利益的目的[14]。
1.2 国内外研究现状
早在上个世纪的七十年代开始,装箱问题就受到了非常广泛的重视,与此同时,与之相关联的科研工作的开展从未中止过。但是,如果说到装箱问题的起源,则可以追溯到更早的时间点。在1831年时,高斯对布局一类的问题开始了研究,归根结底,布局和装箱的研究可以归结为一类,这两个问题的本质是一样的。后人们从未放弃过努力,在前人的研究的基础上开展了大量的工作。然而,付出的努力还是远远不够的,对这一问题的解决至今还没有一套完整的体系,理论尚未成熟[6]。
装箱问题是典型的NP-HARD问题,求解的思路有很多,其中最经典的有:其次适配(Next Fit,NF)算法,首次适配(First Fit,FF)算法,最佳适配(Best Fit,BF)算法,最坏适配(Worst Fit,WF)算法。还有一些常用的算法,包括有界空间(Bounded Space Algorithm, BSA)算法,降序首次适配(First Fit Decreasing,FFD)算法[4],降序最佳适配(Best Fit Decreasing,BFD)算法,降序重构首次适配(Refind First-Fit Decreasing,RFFD)算法,降序改善首次适配(Modified First-Fit Decreasing,MFFD)算法等[13]。
除其次适配(Next Fit,NF)算法,首次适配(First Fit,FF)算法,最佳适配(Best Fit,BF)算法,最坏适配(Worst Fit,WF)算法等研究思路以外,蚁群算法也是一种非常高效的的优化算法[5]。基于蚁群算法的优化方案也被广泛应用,而且优化的结果常常要比其他的算法更好[7][11][12]。比如说,与一维装箱问题比较类似的有一维下料问题,在利用蚁群算法进行一维笑料问题的优化求解时,与其它的算法相比较的话,可以得到更加优化的模型和更令人满意的仿真结果,进一步的减少了材料的浪费和节省了成本[8][15]。因此,可以作为一个参考,将蚁群分析法融入到一维装箱问题的解决中来,寻求更加优化的装箱方案[9]。
1.3研究内容及技术方案
1.3.1研究内容
本文的主要内容就是基于蚁群分析法的一维装箱问题的解决[10]。查阅蚁群算法和一维装箱的相关资料,通过MATLAB建立一维装箱问题的数学模型,结合蚁群算法对数学模型进行求解,并且进行仿真实验[1][2][7]。采取多组实际算例进行实验仿真,并对可能影响实验结果的因素进行讨论和分析,给出总结。
1.3.2技术方案
(1)建立一维装箱问题的数学模型,借助MATLAB,基于蚁群算法对该模型进行求解。
(2)完成相关的仿真实验,通过多个算例对对第(1)点中实现的算法进行仿真验证和分析。
(3)对得到的仿真结果进行分析,对编写的算法进行分析和总结,寻找不足和进一步的解决方案、思路。
第2章 一维装箱问题
2.1装箱问题概述
装箱问题一般来讲,就是将小物品装入大箱子中去。但是,装箱子并不只是单纯的表示将物品装入箱子即可,是要讲究方式和方法的,如何装才能利用最少的箱子装下最多的物品,最大限度的减少箱子空间的浪费现象,实现利益的最大化,这也是研究装箱问题的目的所在和一直以来的追求。
随着社会经济的高速发展,装箱问题的情况越来越复杂,要求越来越多,对装箱的效益也提出了更高的要求。而且,装箱问题不仅仅只是装箱而已,材料切割问题也可以抽象的理解为装箱问题,它们的原理都是非常相似的,材料切割可以看做是逆向的装箱问题。其它诸如此类的问题都可以采用装箱的思想来考虑和解决,所以装箱问题在现实生产中的作用是非常重要的。因此,与装箱问题相关的研究不断展开和深入,装箱问题也在不断地发展着,新的算法也被不断地尝试着引入到装箱问题的研究中去。
装箱问题包含了一维装箱、二维装箱和三维装箱:一维装箱在装箱问题的解决过程中,只考虑一个因素,例如物品的长度或者大小或者重量,相对而言比较简单,因为只需要考虑一个因素即可。二维装箱可以看做是一维装箱问题的拓展或者说是复杂化,要求的因素由一个变为了两个,例如需要同时考虑物品的长度和高度,同理三维装箱文题要求的因素就更多了。要求的因素越多,越贴近实际应用,越符合实际情况,但处理起来也会更加复杂。本文主要就解决一维装箱问题的优化进行说明,更高维度的装箱问题不再在本文中过多赘述了,相关具体内容可以参考相关文献[13]。
2.2一维装箱问题涉及的因素
一维装箱的问题研究的要素是单一的,可以是箱子和物品的长度,也可以是箱子和物品的大小,也可以是箱子和物品的重量,总而言之,只需要考虑一个方面即可。接下来将对一维装箱的问题进行具体的描述:t个待装物品的集合是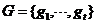 ,假定每一个物品
,假定每一个物品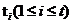 的长度或重量或者大小为
的长度或重量或者大小为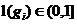 ,而
,而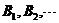 为无数个箱子,箱子的容量为1,并且要求每一个物品个体能切只能装入一个箱子中去,除此之外还要满足装入箱子的物品的总计量量(长度或重量或者大小)不能超过1,最少的开箱数则是装箱的优化目标。利用0-1整数线性规划,可以用下列的公式进行数学描述:
为无数个箱子,箱子的容量为1,并且要求每一个物品个体能切只能装入一个箱子中去,除此之外还要满足装入箱子的物品的总计量量(长度或重量或者大小)不能超过1,最少的开箱数则是装箱的优化目标。利用0-1整数线性规划,可以用下列的公式进行数学描述:
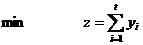 (2.1)
(2.1)
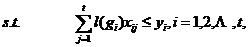 (2.2)
(2.2)
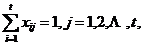 (2.3)
(2.3)
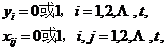
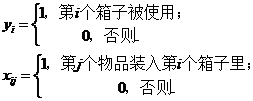
上面就是关于这一问题的数学描述,通过这一系列的公式加上语言描述,我们可以非常清晰地了解这一问题的核心思想是什么。然后,更深层次的研究几乎都是建立在这一原则上,进行进一步深化的。经过科学家们的不断发掘和大量实际案例的检验,目前已经形成了许多比较成熟的算法。一维装箱问题是典型的NP-Problem,到现在为止已经有非常多的相关研究和成果,而且一维装箱问题的发展相对也比较成熟了,有许多经典的解决算法。
2.3一维装箱问题经典算法
求解装箱问题的算法通常被称为装箱算法,有很多解决一维装箱问题的近似算法,这里面最具有代表性和最经典的有下面几个:首次适配算法(First Fit,FF)、其次适配算法(Next Fit,NF)、最好适配(Best Fit,BF)算法、最坏适配(Worst Fit,WF)算法。下面为这四种典型算法的基本原理的大概说明。
(1)其次适配算法(Next Fit,NF)。这种算法是最简单的一维装箱算法,依次对物品集合G中的物品进行处理,从物品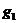 开始,将该物品放置到
开始,将该物品放置到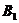 箱子中去。假设现在要进行装箱的物品是
箱子中去。假设现在要进行装箱的物品是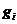 ,令
,令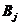 表示指标最高的非空箱子,如果
表示指标最高的非空箱子,如果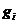 适合装在箱子中
适合装在箱子中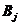 ,则把物品
,则把物品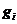 放入箱子
放入箱子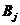 中,否则就放入新的箱子。
中,否则就放入新的箱子。
(2)首次适配算法(First Fit,FF)。这种算法是按照一定的顺序依次处理物品:首先把物品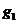 放入箱子
放入箱子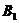 中,再考虑物品
中,再考虑物品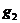 ,若能放入到箱子
,若能放入到箱子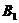 中,则放进去,否则打开一个新的箱子
中,则放进去,否则打开一个新的箱子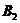 。然后按照相同的方法依序处理各物品,将
。然后按照相同的方法依序处理各物品,将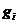 物品放到所有能够放下
物品放到所有能够放下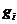 的下标最小的箱子中去,然后把物品
的下标最小的箱子中去,然后把物品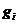 放入新箱子中。其上界最初是由Ullman给出的,并且证明了无论在任何情况下都有下面的公式成立:
放入新箱子中。其上界最初是由Ullman给出的,并且证明了无论在任何情况下都有下面的公式成立:
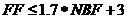 (2.2)
(2.2)
上面公式中的FF和NBF(number of best fit)分别表示首次适配算法和最好适配算法所对应的打开的箱子数量。经历了近四十年的研究Dosa也通过一些实际的算例证明了这一公式的正确性[13]。
(3)最好适配(Best Fit,BF)算法。该算法是按顺序依次来处理物品:首先把物品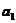 放入箱子
放入箱子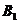 中,再考虑物品
中,再考虑物品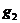 ,如果可以放入到
,如果可以放入到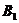 中,则放入
中,则放入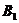 中,否则就打开一个新的箱子
中,否则就打开一个新的箱子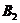 ,然后按照同样的方法依次序处理各个物品。将
,然后按照同样的方法依次序处理各个物品。将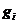 物品放到所有可以够放下而且放置物品后的剩余长度值最小,并且下标是最小的箱子中去。
物品放到所有可以够放下而且放置物品后的剩余长度值最小,并且下标是最小的箱子中去。
(4)最坏适配(Worst Fit,WF)算法。这种算法也是按顺序依次处理物品,只是物品选取箱子时的原则与最好适配算法相反。首先把物品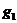 放入到箱子
放入到箱子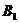 中,再来考虑物品
中,再来考虑物品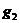 ,如果
,如果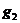 可以放入到
可以放入到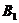 中,则放入到
中,则放入到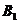 中,否则就打开一个新的箱子
中,否则就打开一个新的箱子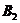 ,然后按照相同的方法依次处理各个物品。将物品
,然后按照相同的方法依次处理各个物品。将物品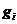 放到所有能够放下而且放置后的剩余长度最大,并且下标值为最小的箱子中[13]。
放到所有能够放下而且放置后的剩余长度最大,并且下标值为最小的箱子中[13]。
在上面列举的几种经典算法之中,第一种算法具有计算快的优点,但是,仅仅是速度快而达不到较好的优化结果是不行的,需要兼顾算法的质量和效率。因此,对经典算法的进一步优化也成为了后来的研究人员的工作重心。经典的算法对于新的研究人员具有非常重要的启发作用,正是由于科研前辈们的研究,我们才能对这一问题有更加深入的认识和理解,这也是科学发展的必经之路。毕竟,从量变到质变是需要一个非常漫长的过程的。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: