基于隐式曲线拟合的超临界压力区变组分天然气混合物热力学性质快速计算方法外文翻译资料
2021-12-26 17:15:47
基于隐式曲线拟合的超临界压力区变组分天然气混合物热力学性质快速计算方法
摘要
在超临界压力下,汽化器被广泛用于液化天然气的再气化。基于模拟的气化器设计时间严重依赖于天然气热力学性质的计算速度,这是由于数百万次热力学性质的迭代。本文提出了一种超临界压力区天然气热力学性质的快速计算方法。本文提出了一种超临界压力区天然气热力学性质的快速计算方法。该方法首先建立了参考组分的计算模型,将超临界压力区划分为三个分段,并基于隐式曲线拟合对每个分段分别进行回归,然后建立了基于组分的隐式曲线拟合方程,将热力学性质计算扩展到n从参考成分到任何可变成分。利用该方法,给出了天然气典型组分(C1、C2、C3、N-C4、N-C5、N2)的计算公式,包括温度170~60℃,压力5~10MPa。本方法比GERG-2008快104倍左右,平均偏差小于0.5%。
关键词:快速计算、天然气、超临界压力、热力学性质、变组分
1.介绍
天然气(NG)是一种清洁的燃料,经常液化用于运输。(Hammer,2004年)。液化天然气(LNG)在用作燃料气之前,必须通过汽化器在超临界压力条件下重新气化为天然气(Han等人,2016a)。气化器效率严重影响了液化天然气再气化工艺的可靠性和运行成本,因此对高效可靠的气化器的设计提出了很大的要求(Fahmy等人,2015)。
对于液化天然气气化器的设计,与基于实验的设计方法(Pacio和Dorao,2011)相比,基于模拟的设计方法是一种有效且低成本的方法。基于仿真的液化天然气气化器设计方法,例如液化天然气气化器的分布参数模型(Pan等人,2016;Pu等人,2014;Qi等人,2016),将调用大量的热力学性质计算,直接决定速度以及汽化器设计的准确性(Melaaen和Owren,1996年;Zudkevich和Gray,1975年)。因此,有必要开发一种满足快速、高精度、绝对稳定性和可逆性要求的气化器内天然气热力学性质的快速计算方法(Ding等人,2005年)。
气化器中的NG有两个不同的特点,包括在超临界压力下工作和由可变成分组成。首先,在进入气化器之前,需要将天然气加压至超临界压力,以降低泵送液化天然气的功耗,现有气化器的压力范围为5至9兆帕(Han等人,2016a;Meng等人,2014a;Meng等人,2014b)。其次,天然气是几种不同组分的混合物,天然气的组成因气田而异(Foeg等人,1998年)。
因此,需要有一种快速计算汽化器内NG热力学性质的方法,能够计算整个超临界压力区内变组分NG的热力学性质。
作为计算热力学性质的现有方法之一,状态方程法(eos)得到了广泛应用,如PR状态方程(彭和罗宾逊,1976)、RKS状态方程(soave,1972)、LKP状态方程(l e e和kesler,1975;plocker等人,1978)和GERG-2008(kunz和wagner,2012)。天然气工艺计算基于简化的材料和热平衡方程,由于其最佳AC*对应作者。在所有方法中对大区域的精确度。然而,当需要大量的性能计算时(例如,设计一个具有分布参数的液化天然气设备),这是非常长的模型(Han等人,2016b;Pan等人,2016;Wang等人,2015)。
查找表法是一种快速的计算方法,它由插值方案和通常由状态方程生成的表组成,因为一旦生成了表,就不需要求解状态方程。但是,有关的参数,如hfrac14;f(p,t)和tfrac14;g(p,h)的计算是根据不同的表格进行的,这些参数是不可逆的(ding,2007)。因此,该方法不适用于数百万热力学性质计算,例如液化天然气气化器的模拟。
为快速、稳定地计算工作流体的热力学性质,开发了隐式曲线拟合和显式计算方法(Ding,2007)。该方法建立隐式三次方程,保证曲线拟合的高精度和可逆性,并以隐式方程的解析解作为快速稳定计算热力学性质的显式公式,如表1所示。
表1
该方法已很好地用于纯制冷剂(例如R22、R134a和R32)和具有固定成分的混合制冷剂(例如R410A和R407C)(Ding等人,2005;Sieres等人,2012;Zhao等人,2009)。该方法的应用范围包括饱和区、过热区、两相区和过冷区(Ding等人,2005;Sieres等人,2012),并扩展到临界压力(Ding等人,2007)和超临界区(Zhao等人,2009)。然而,现有的快速计算制冷剂热力学性质的隐式曲线化方法仅适用于固定组分混合物。
现有的隐式曲线拟合方法适用于固定组分混合料,不能直接推广到可变组分混合料。由于分子间作用力的不同,变组分对天然气混合物的热力学性质有着重要的影响。因此,需要一个新的隐式方程来反映变量组成。
本文提出了一种基于隐式曲线拟合的超临界压力区变组分混合气热力学性质的快速计算方法,能够反映变组分对热力学性质的影响。
2.技术方法路线图
建立超临界压力区天然气热力学性质的快速计算方法,首先建立参考组分的计算模型,然后建立基于组分的隐式曲线拟合方程,将热力学性质计算从参考组分扩展到超临界压力区天然气的热力学性质计算。NY可变成分。本方法的详细假设包括:1)等温线上热力学性质随压力的变化是连续的;2)等温线上热力学性质随温度的变化是连续的;3)不同组分混合物的热力学性质随温度的变化是连续的。组成是连续的。
基于隐式曲线拟合的超临界压力区变组分混合气热力学性质快速计算方法的详细过程包括以下两个步骤:
1)开发用于参考成分的隐式曲线拟合模型,包括三个子步骤:
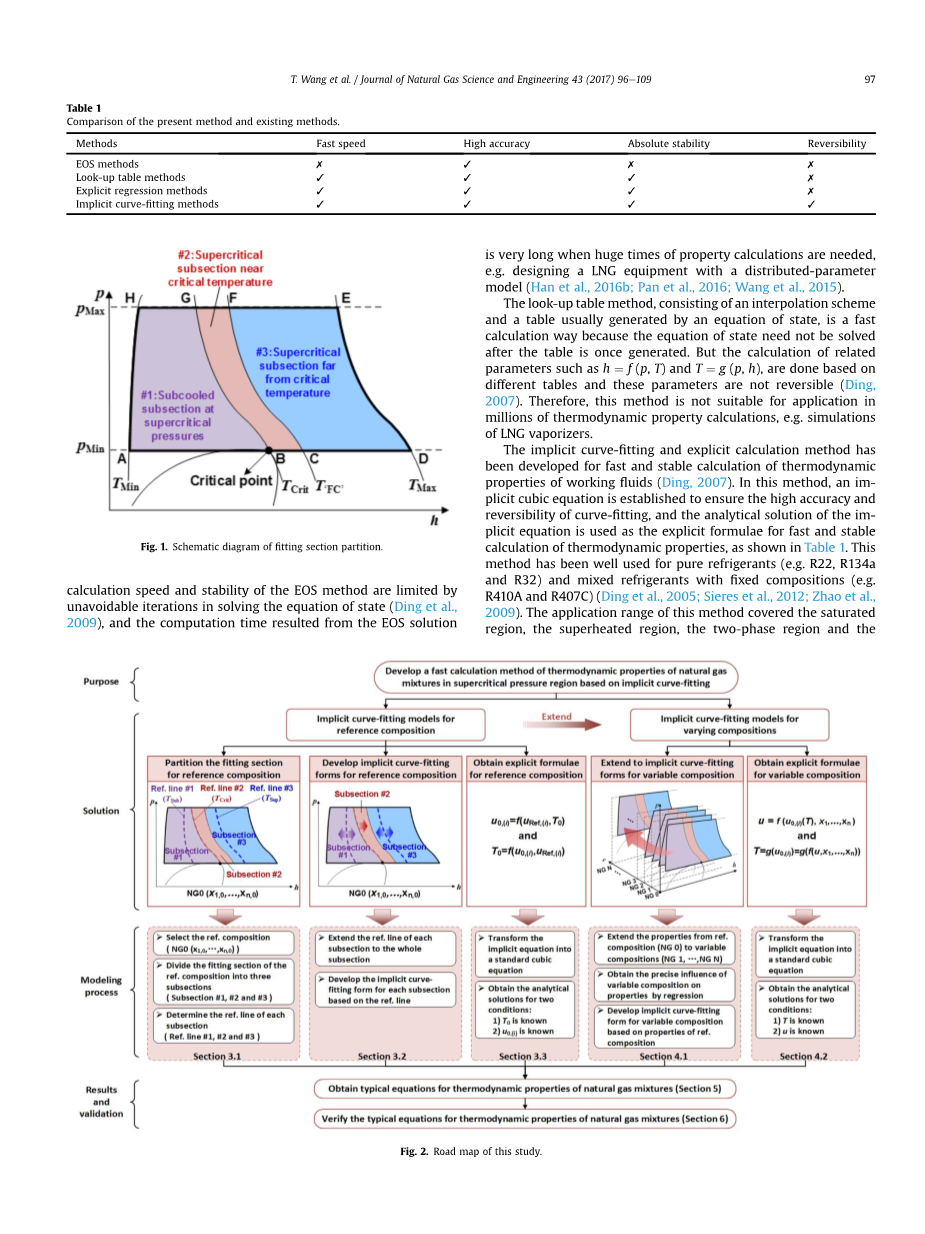
i)对配件部分进行划分,以供参考组成。选择经典NG的组成作为参考组成,参考组成的拟合段分为图1所示的三个小节,确定每个小节的参考线。
图1
ii)开发用于参考成分的隐式曲线拟合形式。以参考线为基础,得到各分段的隐式曲线拟合形式,用于参考组合。
iii)获得参考成分的显式公式。将隐式曲线拟合方程转化为标准三次方程,并将其解析解作为参考成分的显式公式。
(2)扩展到变量组合的隐式曲线拟合模型,包括两个子步骤:
i)建立变量组合的隐式曲线拟合形式。首先,将参考组分的热力学性质推广到变量组分;其次,通过隐式曲线拟合得到变量组分对热力学性质的精确影响;第三,根据参考组分的热力学性质,建立了变量组分的隐式曲线拟合形式。参考成分NG混合物。
ii)求出变成分的显式公式,将变成分的隐式曲线拟合方程转化为标准三次方程,并将标准三次方程的解析解作为变成分的显式公式,避免了求简单化根的迭代。CIT曲线拟合模型。详细的技术路线图如图2所示。
图2
为了获得天然气混合物在超临界压力区的热力学性质,需要参考组分(u0,(i))的每个分段的热力学性质和可变组分(u)的每个分段的热力学性质,并且可以通过开发1)隐式曲线拟合模型得到参考组合和2)变量组合的隐式曲线拟合模型。
三.用于参考成分的隐式曲线拟合模型
3.1.为参考成分安装分区
选择一种常用的天然气混合物成分作为参考成分,将参考成分的拟合段分为三个部分,包括超临界压力下的过冷段、临界温度附近的超临界段和远离临界温度的超临界段。初始温度,分别在图1中显示为“abgh”、“bcfg”和“cdef”。超临界区近将热力学性质发生显著变化的临界温度作为单独的分段进行回归,以保证该区域的拟合精度。
对于上述每个分段,基准线的确定是分段曲线拟合方法的关键。对于超临界压力下的过冷段和远离临界温度的超临界段(分别显示为lsquo;abghrsquo;和lsquo;cdefrsquo;,如图1所示),参考线是一个等温线,在该等温线上,与温度有关的焓或熵的二阶导数达到最大值,如等式所示。(1)—(2)。对于接近临界温度的超临界分段(如图1中的“BCFG”),引入临界温度的等温线作为分段的参考线,并根据tsup - t#39;fc = 3~5摄氏度确定分段的边界线(如图1中的曲线fc)。
式中,tsub和tsup分别是超临界压力下过冷段和远离临界温度的超临界段的参考状态;t是温度;u是除温度和压力外的热力学性质,如焓、熵等;tcrit是临界温度;tmax和tmin是配件范围内的最大值和最小值。
根据纯制冷剂参考线的隐式形式(Zhao等人,2009年),采用上述选定的参考线作为参考状态,由式(3)描述,建立了天然气各分段参考线的隐式曲线拟合模型。
(3)
式中,Uref,(i)是除参考线温度和压力外的热力学性质,或其变换(如Uref,(i) = f(Href,(i))等);Vref,(i)是p0的函数;a1,(i) ~ a8,(i)是拟合系数。
为了得到各分段参考线隐式曲线拟合模型的显式公式,将式(3)转化为标准三次方程,如式(4)所示,其中y代表热力学性质uref,(i)在p0压力下,a、b、c和d的详细函数由式(5)描述。解决情商问题。式(4),(5)可以产生一个合适的根(Ding等人,2005),并且可以得到明确的公式Uref,(i) = f(p0)。
其中,y是未知的热力学性质;a、b、c和d是标准三次方程的多项式系数。
3.2.用于参考成分的隐式曲线拟合形式
在参考线的基础上,建立了各分段参考组合的隐式曲线拟合模型。参考成分隐式曲线拟合模型的形式与纯制冷剂相似(赵等,2009),如式(6)所示,不同之处在于参考线的选择,如式(7)所示。
(6)
式中,a1,(i)~a11,(i)为回归系数;t为温度;u为除温度和压力外的热力学性质,或其变换(如u=f(h)等);下标ref、crit、sup、sub和fc为参考线、临界温度、远离临界温度的超临界分段、过冷子CTI。在超临界分段上,边界线分别远离临界温度;下标0代表参比组分NG的热力学性质;下标(i)代表各拟合段。
3.3.参考成分的显式公式
为了避免隐式曲线拟合模型求解过程中的迭代,需要给出各分段参考组合隐式曲线拟合模型的显式公式。为了得到明确的公式,参考成分NG p0的压力,以及温度t0或另一个热力学性质u0,(i)(如焓h0,(i),熵s0,(i)和密度r0,(i)需要已知,t0和u0,(i)可以通过解式(6)得到。众所周知,式(6)转化为如式(4)所示的标准三次方程,式(8)描述了a、b、c和d的详细函数,然后通过求解方程(4)和(8)得到了u0,(i)。如U0,(i)所知,将式(6)转换为如式(4)所示的标准三次方程,其中a、b、c和d的详细函数由式(9)描述,然后通过解方程(4)和(9)得到T0。
(8)
(9)
式中,y是未知的热力学性质;a、b、c和d是标准立方方程的多项式系数;a1,(i)~a11,(i)是拟合系数;tref,(i)是参考线的温度;uref,(i)是参考线在p0压力下的热力学性质;t0是温度,u0,(i)是热机分段的热力学性质。
4.变量组合的隐式曲线拟合模型
4.1.变量组合的隐式曲线拟合形式
根据参考组分的热力学性质,通过拟合变量组分对热力学性质的精确影响,分别建立了各分段的变量组分隐式曲线拟合模型。详细模型如等式(10) - (13)所示,解释如下:
(1)由于三次多项式可以解析求解,因此曲线拟合形式采用三次多项式,与二次多项式相比,能保证更高的拟合精度
(2)以参考组分的热力学性质作为拟合参考,因为天然气中甲烷的摩尔分数大于80%,且可变组分热力学性质的变化趋势与参考组分的变化趋势相似(foeg等人,1998年;Park和Cho,2016年)。
(3)Ng的组成作为一个独立变量使用,因为可变组成Ng的热力学性质与Ng的组成直接相关。
(10)
式中,u表示除p和t以外的热力学性质;p和t分别表示压力和温度;x1~xn表示每种组分的摩尔分数,用于可变组分ng;x1,0~xn,0表示每种组分的摩尔分数,用于参考组分;a1~a3n_2、b1~bn和c1~cn表示拟合系数;下标crit rep表示临界参数,下标0表示参考组分ng,下标(i)表示每个分段;f0,(i)是计算参考组分NG各分段热力学性质的函数;n是NG的分量数。
4.2.变量组成的显式公式
为了避免隐式曲线拟合模型求根的迭代,必须给出各分段变量组合隐式曲线拟合模型的显式公式。为了得到明确的公式,需要知道Ngx1~xn的组成、压力p以及温度t或其他热力学性质u(如焓h、熵s和密度r),通过解方程可以可逆地得到t和u。
众所周知,变量组分的pcrit和tcrit由式(13)计算,首先;其次,根据式(12)得到参考组分对应的p0和t0;第三,通过解式(11)得到参考组分的u0,(i);第四,P和T的变量组分的u由转化得到。将式(10)转化为标准三次方程,如式(4)所示,式(14)描述了a、b、c和d的详细函数。
(14)
式中,y是未知的热力学性质;a、b、c和d是标准三次方程的多项式系数;a1,(i)~a3n_2,(i)是拟合系数;x1~xn是可变组分NG的每个组分的摩尔分数;u0,(i)是参考组分NG的热力学性质;n是组分NG的个数。
众所周知,u0(i)通过将式(10)转换为标准三次方程得到参考成分,如式(4)所示,其中a、b、c和d的详细函数由式(15)描述;其次,变量成分的pcrit和tcrit由式(13)计算;第三,参考成分的相应p0和t0由式(13)计算。用公式计算了稀土元素的组成。(12)和(11);第四,根据式(12)得出变量组分的t。
式中,u是除p和t之外的热力学性质。
5.天然气混合物热力学性质的典型方程
计算天然气混合物热力学性质的方法可以应用于整个超临界压

英语原文共 14 页
资料编号:[3464]




