基于粒子滤波的电动汽车用锂离子电池SOC估算毕业论文
2020-04-10 16:53:41
摘 要
进入21世纪以来,环境污染、能源危机等问题逐渐受到世界各国关注,在环保节能方面表现良好的电动汽车,也受到了人们越来越多的重视。电池荷电状态(SOC)是电动汽车内部电池管理系统中非常重要的参数,SOC的准确估计对电动汽车电池有效利用率的提高、电池使用寿命的延长以及电动汽车续航里程的增加都有着重要的意义。粒子滤波是一种基于蒙特卡罗方法的滤波方法,可以应用于受到非高斯分布噪声影响的非线性系统,与实际锂离子电池模型相匹配。
本文以镍钴铝酸锂三元锂电池(NCA电池)为研究对象,基于简化电化学模型建立锂离子电池模型,其中的未知参数,通过最小二乘法来进行辨识,采用粒子滤波算法,利用实测数据,在MATLAB软件中对锂离子电池SOC进行了估算,粒子数为400时估算值与真实值的相对误差值最大为2%左右,结果表明粒子滤波算法可以完成较准确的估计结果。
关键词:粒子滤波;SOC估算;锂离子电池;电池模型
Abstract
Since the 21st century, such problems as environmental pollution, energy crisis has caught the world’s attention. People attach great importance to electric cars which performed well in terms of environmental protection and energy saving. The battery state of charge (SOC) is a very important parameter in the internal battery management system of electric vehicles. The accurate estimation of SOC is of great significance to the improvement of the effective utilization rate of electric vehicle batteries, the extension of battery life and the increase of the range of electric vehicles. Particle filter is a filtering method based on Monte Carlo method. It can be applied to nonlinear systems affected by non-Gauss distribution noise. It is suitable for the actual lithium ion battery model.
The research object of this paper is Nickel Cobalt Aluminum Oxide (NCA) battery. Based on the simplified electrochemical model, a lithium ion battery model is established. Least-square method is used to identify the system’s unknown parameters. In this paper, particle filter algorithm is used in MATLAB software to estimate the SOC of lithium ion battery with measured data. The maximum relative error between the estimated value and the true value is about 2% when the number of particles is 400. The result shows that the particle filter algorithm can obtain more accurate estimation results.
Key Words: particle filter; SOC estimation; lithium-ion battery; battery model
目 录
摘 要 I
Abstract II
第1章 绪论 1
1.1背景及意义 1
1.2国内外研究现状 1
1.3研究内容和技术方案 2
1.3.1基本内容 2
1.3.2技术方案 2
第2章 锂离子电池工作原理及估算方法 3
2.1锂离子电池的工作原理 3
2.2电池SOC的定义 4
2.3常用的电池SOC估算方法 4
2.3.1安时法 5
2.3.2内阻法 5
2.3.3开路电压法 5
2.3.4神经网络法 6
2.3.5卡尔曼滤波法 6
2.3.6粒子滤波 7
2.4本章小结 7
第3章 锂离子电池模型的选择与参数辨识 8
3.1常用的电池模型 8
3.1.1等效电路模型 8
3.1.2神经网络模型 10
3.1.3电化学简化数学模型 10
3.2电池模型的选择 11
3.3模型参数辨识 12
3.3.1最小二乘法 13
3.3.2参数辨识结果 14
3.4本章小结 14
第4章 基于粒子滤波的锂离子电池SOC估算 15
4.1粒子滤波算法 15
4.1.1贝叶斯估计 15
4.1.2蒙特卡罗方法 16
4.1.3贝叶斯重要性采样 16
4.1.4序贯重要性采样 17
4.2粒子退化 18
4.3重采样 19
4.4粒子滤波估计电池SOC的算法设计及实现 19
4.5估算结果 20
4.6本章小结 22
第5章 总结和展望 23
5.1全文工作总结 23
5.2展望 23
参考文献 24
致谢 26
第1章 绪论
1.1背景及意义
随着社会发展,全球人口量增多,能源消耗以及环境问题日益严重,传统汽车因其对石油的严重消耗以及其导致的排放污染,而在这两个方面的固有劣势显现地愈发明显,电动汽车因在这两个方面的优势而越来越被人重视,世界各国都加强了对电动汽车的开发研究,而作为电动汽车动力之源的电池技术发展更是重中之重。锂离子电池以其寿命长、功率承受力大、能量密度高以及温度适应性强等特点,在电动汽车中得到了广泛应用。而电池荷电状态SOC(State of Charge)的精确获知,对于电池管理系统BMS(Battery Management System)而言具有重要意义,它直接影响了电池组的安全性、可靠性以及使用寿命。通过SOC的准确估计,我们可以对电池进行均衡充电,保持电池组各个电池性能均匀,从而延长电池使用时间;避免对电池的过充电或过放电;能量管理系统对能量进行合理分配,提升电能利用率;依据SOC对电动汽车行驶里程实现准确预测,提供合理驾驶策略的选择依据。
但是在电动汽车的实际工况中,电池所处的工作环境十分复杂,受到充放电电流电压变化、工作温度波动、电池老化、循环寿命等影响,因而SOC的准确估计已经成了电动汽车发展中急需解决的一个问题[1]。
1.2国内外研究现状
对于电池管理系统而言,准确估算电池SOC并将之准确反映给用户,是其必备功能,国内外关于估计电池SOC的方法有很多研究成果。
首先关于SOC的定义,传统定义为电池最大可用容量与其标称容量之比,何正伟、付主木[2]提出用能量守恒原理来重新定义其概念,提升了电池SOC的估计精度,降低了估计复杂度,并且能够匹配大电流、变电流放电工况。高建树[3]等人也重新定义了SOC并引入SIR粒子滤波算法估算SOC,达到了更高的精度及适应。
几十年来,学者们提出了很多SOC的估计算法,如内阻法、安时积分法、开路电压法、神经网络法、线性模型法、卡尔曼滤波法、粒子滤波系列算法等现在常用方法[4]。其中,内阻法通过电池交流内阻、直流内阻与SOC的关系来计算,在放电后期表现良好,但它只适于特定放电工况下,另外影响内阻变化的因素有很多;安时积分法只需要知道初始SOC和实时测量回路电流,但缺陷在于受初值误差影响大,且电流测量引起的误差将会得不到补偿将越来越大,无法解决电池的自放电问题,使得其一般需要其他算法辅助估计;开路电压法需要测定开路电压,通过电池SOC与电动势之间的数学关系计算出电池SOC,方法简单,精度较高,但需要较长静止时间,不适用于SOC实时估计;神经网络法在使用中将持续对模型参数值进行更新,这令它宜于在线估计,然而在运行前它需要用很多电池数据进行训练,且训练需要一定时间,同时所用数据和训练手段都极大影响着估算精度;卡尔曼滤波法可以将电池 SOC 的估算值和估算误差的协方差一起输出,相对于其他方法,准确性显著提升,但它大大依赖于电池模型的准确性,且建模及算法都比较复杂,对系统噪声有要求[1,5];粒子滤波是近十几年逐渐发展起來的一种基于蒙特卡罗方法的可以应用于非高斯、非线性时变系统的滤波方法,根据重要性采样原则,用粒子的概率分布代替了未知的后验概率密度,这令其能处理非线性系统,以及非高斯分布的噪声,正好适于电池SOC估算[6,7]。粒子滤波算法有重采样的步骤,吴兰花[8]等人在这之前进行了基于BP神经网络的权值调整,通过加大处于概率分布尾部的粒子的权值,提高了样本粒子的多样性,减小了对SOC的估计误差。郭辉[9]提出了一种改进的自适应粒子滤波的算法,该方法提高了传统自适应粒子滤波的鲁棒性,提升了对SOC的估计精度。
1.3研究内容和技术方案
1.3.1基本内容
本文将针对动力电池荷电状态SOC的估计算法——粒子滤波算法进行研究,基于锂电池外特性的实验数据,建立合适的电池模型,用线性回归的方法来辨识模型参数。在MATLAB软件中构建电池模型,并研究粒子滤波算法(PF)在估计SOC中的应用,进行试验验证。
1.3.2技术方案
具体技术方案如下:
(1)阅读国内外相关文献,了解估计动力电池荷电状态SOC的各种方法,掌握典型粒子滤波算法的原理和实现手段,了解国内外粒子滤波算法的发展。
(2)参考电化学简化数学模型、戴维南模型、PNGV模型等具有代表性的电池模型,最终选择电化学简化复合模型,使用线性回归的方法来辨识模型参数,在MATLAB中搭建电池模型。
(3)设计粒子滤波算法的具体程序,选定合适参数,并在MATLAB中进行试验,给出SOC估计结果,将估计值与参考值对比,给出估计精度并做出评判。
第2章 锂离子电池工作原理及估算方法
了解锂离子电池的工作原理,对其有基本认知,有助于进行电池SOC估算。了解电池SOC的定义以及常用的电池SOC估算方法,也有利于进行估算方法的深入研究。
2.1锂离子电池的工作原理
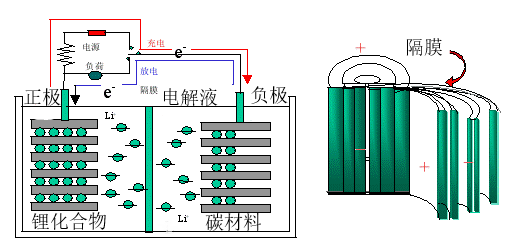 锂离子电池是一种二次电池,采用了能够嵌入、脱嵌锂离子的化合物材料制作而成,可以循环充电使用。它通过锂离子在两极间的往复嵌入,完成电流的产生。其结构一般由正负极、隔膜与电解质等组成。正极材料一般是含锂的化合物,负极则基本上是碳素材料。
锂离子电池是一种二次电池,采用了能够嵌入、脱嵌锂离子的化合物材料制作而成,可以循环充电使用。它通过锂离子在两极间的往复嵌入,完成电流的产生。其结构一般由正负极、隔膜与电解质等组成。正极材料一般是含锂的化合物,负极则基本上是碳素材料。
图 2.1 锂离子电池工作原理
锂离子电池正极材料,主要采用、、和等锂化合物。LiMn2O4优点在于其合成简单、价格低廉,但其缺点是在进行可逆反应时,嵌入、脱嵌的锂离子量较少,这导致其容量偏低。LiCoO2优点在于释放电压平缓、容量高、性能可靠寿命长,缺点是钴(Co)来源较少,钴化合物价格较贵并且毒性较大。一般认为用Ni取代LiCoO2中的Co可以降低成本,取得更好的效果。在新能源汽车发展的早期,电池一般采用磷酸铁锂电池,近年来在电动汽车上应用更多的是三元电池NCM和NCA,分别使用了镍钴锰和镍钴铝三种材料作为正极材料,三元锂电池最大的优势在于其能量密度高,更符合电动汽车对轻量化和续航里程方面的要求,其中NCA电池技术门槛较高,在我国发展较慢。
锂离子电池的负极,一般使用天然石墨等锂碳化物等材料来代替金属锂。碳材料来源广泛,成本低廉,没有毒性。通过锂离子在碳中的结合与分离进行充放电过程[10]。
以NCA电池为例介绍锂离子电池工作原理:电池在充电时,正极材料被氧化,负极材料被还原,锂离子从正极材料的晶格中脱出,经过电解液和隔膜嵌入到负极中;放电时,锂离子从负极脱出,经过电解液和隔膜再嵌入到正极材料的晶格中。
电极反应式如下(正向为充电,逆向为放电):
正极:
负极:
电池:
2.2电池SOC的定义
电池荷电状态即SOC(State of Charge),数值为电池剩余电量与总电量的比值,表征了剩余电量的百分比。国内外对电池SOC的定义并未有明确统一,目前一般将 SOC 定义为电池的剩余电量与最大可用容量(相同放电倍率下)的比值:
式中,:电池剩余可用的电量(A·h)
:恒流放电情况下电池的最大可用容量(A·h)
通常将电池在一定温度下充满电的状态时的SOC定为100%,电池完全放电之后的SOC值定为0。
电池SOC不能够通过定义直接计算得到,需要用电池的其它参数来对其估算,这是因为在电池的实际使用中,受到了电压、电流,环境温度,充放电倍率,电池老化程度等因素的变化影响[9]。
2.3常用的电池SOC估算方法
随着电动汽车产业的蓬勃发展,电池管理系统的研究受到了更多的重视,电池SOC的估算是其核心的一部分,近年来,出现了很多经典的SOC估算方法,人们也在不断追求更精准实用性更好的估算方法,这里介绍一下常用的SOC估算方法。
2.3.1安时法
安时法,又称为电荷累积法,是估算SOC的经典方法[11],它根据一定时间内,电池充放电电量的统计,在上一时刻SOC基础上进行累计来得到当前状态的SOC:
式中::当前状态的SOC值
:初始状态的SOC值
:电池的额定容量(A·h)
η:库伦效率
I:电池工作电流(A)
安时法估算SOC,只需要知道其初始值和电路中实时电流即可,因其简单、可靠,适用性广的特点得到广泛应用,不过它的缺点表现为以下三个问题:
(1)计算需要一个可靠的初始值,初始值存在误差将无法修正;
(2)电流值的测量依赖于传感器的精度,测量会受到传感器自身误差、外界环境误差等因素影响,产生的误差在式中积分不断累积,导致其误差越来越大;
(3)无法解决电池可能存在的自放电问题,SOC估计时产生的误差,会给电池带来一定伤害,可能会令电池过量充、放电。
2.3.2内阻法
锂离子电池内阻,具体包括直流内阻与交流内阻,大量实验表明,电池内阻与电池SOC值有关,基于这个关系,可以利用电池内阻值来估算出电池SOC,公式如下:
但该方法存在以下问题:
(1)估算所需的交流内阻,在电动汽车上难以获取;
(2)由于电池老化程度、工作温度以及各种化学因素的影响,电池内阻值会不断变化;
(3)由于制作工艺的不稳定,即使是同一型号电池内阻都会存在差异,型号不同的电池内阻差异更大,该方法无法达成计算SOC值的需求精度。
2.3.3开路电压法
电池处于静态或无负载状态时, 开路电压和SOC存在一定的对应关系, 因此, 在对电动汽车电池SOC估算时,需要电动汽车充分静置后,通过获取开路电压将之传递给BMS,来估计电池状态[12]。该方法适合在汽车不工作时使用。
该方法存在以下问题:
(1)充放电过程中无法直接得到开路电压值,所以电动汽车上使用时,需要脱离工作状态很长时间,这种延期性对电动汽车而言并不合适;
(2)由于在电池充放电初期和末期的时候电压变化较大,此时估算精度比较高,其它时候精度比较差,所以不适合单独估算电池的SOC值,本文中使用开路电压法来解决SOC的初值问题。
2.3.4神经网络法
神经网络法通过模拟人脑思维,同时处理多个数据项,计算后输出所求的函数。神经网络结构由基本的输入层、输出层以及隐含层构成。在估算电池SOC时,输入量一般是电压、电流、内阻和环境温度等参数,输出量是电池SOC值。该类方法通过构造非线性单元,构造出每一个变量和电池 SOC 相应的联系,不需要初始值,处理数据速度较快,适用于各种类型电池[13]。
该方法存在以下缺点:
(1)建立神经网络系统复杂,需要采集大量的理想样本实验数据来建立模型;
(2)该方法的训练对时间和计算量有很大要求,另外一大缺点是当参数变异,引起系统状态波动时,它并不能很好地应对因此产生的谬误。所以目前该预测方法比较难于用到实际环境中运行。
2.3.5卡尔曼滤波法
二十世纪实际中叶,R. E. Kalman提出来卡尔曼滤波(Kalman filtering,KF),该方法将状态空间分析方法与滤波理论融合,能够很好地应对动态系统中出现的不确定干涉。该算法本质上是一种递推算法,利用估算的状态向量上一时刻的估算值与实时观测向量值,对状态向量作最小方差估算[14]。
状态方程:
观测方程:
在估计电池SOC时,电池电流、电池内阻、环境温度、剩余容量等参数可以作为系统输入变量,系统的输出量为工作电压。卡尔曼滤波法相较于传统方法,计算机上运算量、存储量大为减少,具有实时性良好的特点,受到广泛应用,缺点是卡尔曼滤波在实际运用中对硬件的能力有硬性需求,且不能处理非线性问题。一种被称为扩展卡尔曼滤波(EKF)的方法,通过数学手段完成了系统从非线性到线性化的转变,之后再使用KF。该算法运行过程中,计算量较小,受到了研究者更多关注,这种方法需要模型中的系统噪声和观测噪声是高斯白噪声,但在实际使用中,锂离子电池的噪声分布是不确定的,这大大影响了KF的估计结果[15]。还有一种称为无迹卡尔曼滤波(UKF)的方法,基于无迹变换与EKF框架,又有很大改进,但是仍受限于高斯分布条件。
2.3.6粒子滤波
粒子滤波,又名贯序的蒙特卡罗方法,它利用粒子集来表示概率,可以用在任何形式的状态空间模型上,核心思想是通过从后验概率中抽取的随机状态粒子来表达其状态分布,是一种顺序重要性采样法(Sequential Importance Sampling)。它的优点是能有效处理任何线性或者非线性的系统模型、高斯或者非高斯的噪声模型。
关于粒子滤波的详细原理以及实现过程,将在第4章进行详细介绍。
2.4本章小结
本章首先介绍了锂离子电池的工作原理,包括正负极所用材料、充放电过程;然后介绍了电池SOC的一般定义,以及估算SOC的一些经典方法,关于粒子滤波算法,在第四章进行详细介绍。
第3章 锂离子电池模型的选择与参数辨识
3.1常用的电池模型
进行电池SOC估算,需要挑选合适的数学模型,模型要阐述电池工作特性与影响因素之间的关系,需要考虑到电池电压、电流、内阻、环境温度等,通过相关参数的获取,实现SOC的估算。




